二叉树OJ

最新推荐文章于 2024-07-19 15:45:46 发布

Epiphanywh

最新推荐文章于 2024-07-19 15:45:46 发布

阅读量130

点赞数 7

文章标签：算法数据结构

本文链接：https://blog.csdn.net/2201_75479723/article/details/133143902

版权

（一）根据一种/两种遍历结果，求其余遍历情况

1）已知的遍历结果给出了空树的位置

这种题型给出的条件一般是以下形式（其中#代表空格，下面我为了方便，我将给出的条件整体用一个数组描述）：

假设给出的条件是用前序遍历获得的结果，由此构建原先树的思想如下：

先来说一下构建树的递归思想，例如构建下面这棵树：

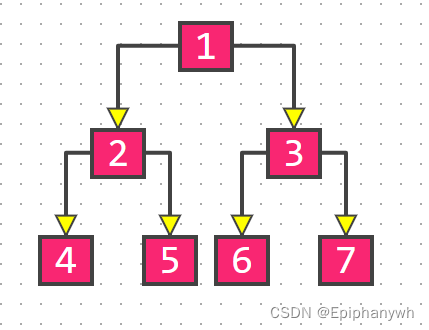
将构建整棵树拆分成若干个小问题：整棵树是由根节点1和左右子树组成的，而左子树也是由根节点2和左右子树组成的，右子树也是由根节点3和其左右子树构成的。

又因为整棵树最小可以拆分成以4为根节点的树：它的左子树是空，这也就意味着左边不会再向下构建子树了（4的左子树构建完成）；它的右子树也是空，那么右边也不会再向下构建子树了（4的右子树构建完成）。当左右子树构建完成后，4这整棵树也就构建完成了。

而4这颗树又是2的左子树，4这棵树构建完成也就是2的左子树构建完成，当2的右子树构建完成，2这颗树才算构建完成。以此类推，直到1的左右子树构建完成，整棵树就构建完成了。

构建步骤：

前序遍历结果的第一个值是由根节点得到的
根节点构建成功后，
- 构建左子树：
  - 如果用于构建节点的值为#，则说明左子树根节点为空，既然根节点为空，那整棵树也为空，左子树构建完成；
  - 如果用于构建节点的值不为#，则说明左子树的根节点的值为该值，然后继续构建其子树（子树分为左子树和右子树，构建左子树则同样使用 “构建左子树” 这个步骤）；
- 构建右子树：
  - 如果用于构建节点的值为#，则说明右子树根节点为空，既然根节点为空，那整棵树也为空，右子树构建完成；
  - 如果用于构建节点的值不为#，则说明右子树的根节点的值为该值，然后继续构建其子树（子树分为左子树和右子树，构建左子树则同样使用 “构建左子树” 这个步骤）；
重复步骤二，直到根节点的左右子树构建完成，那么整棵树就被还原出来了。

构建左子树的基本步骤如下：

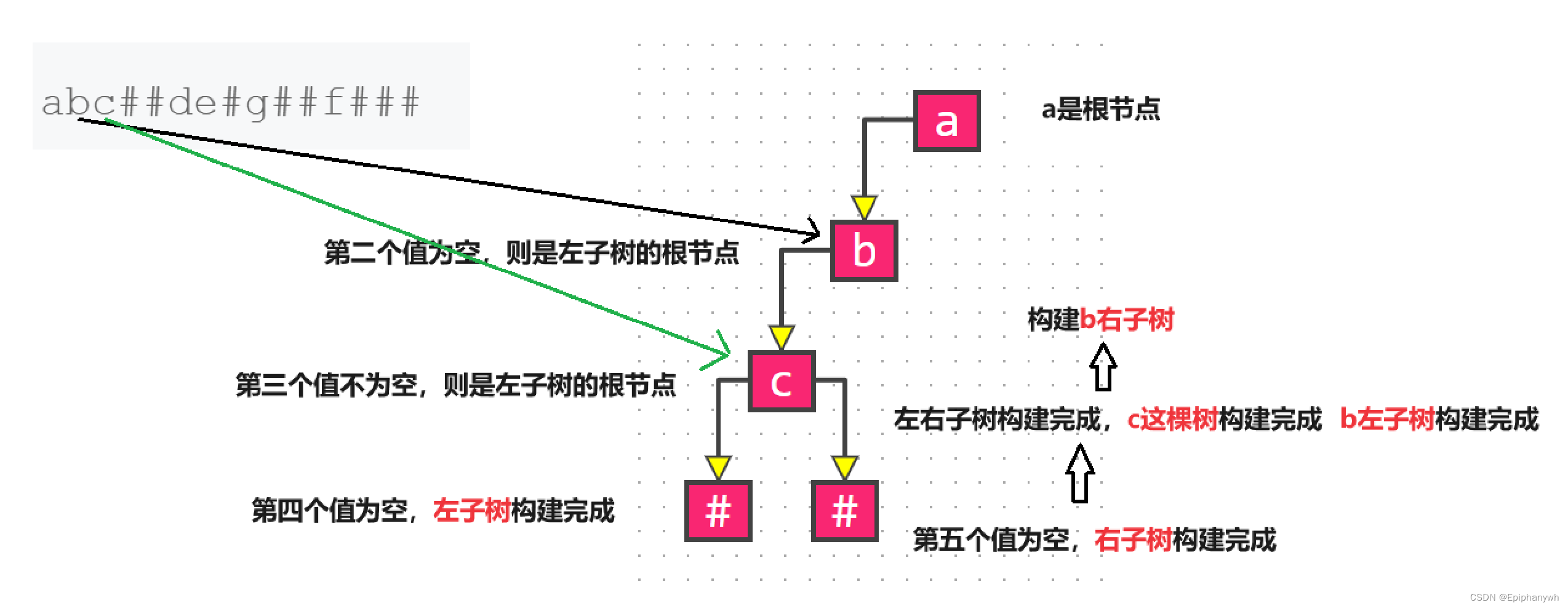
构建右子树的基本步骤如下：

最终树的形状是：

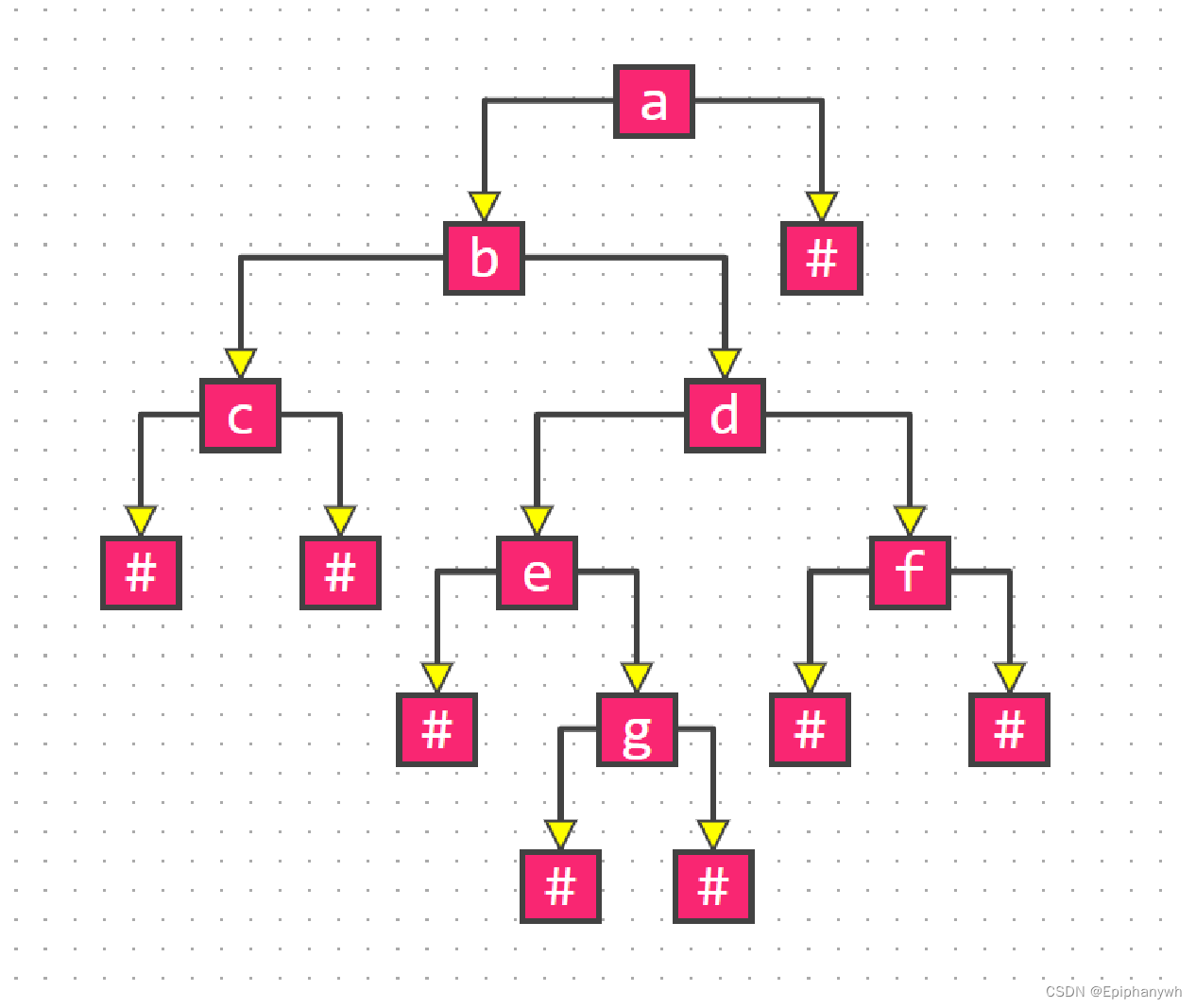
当然，后序遍历和中序遍历是同样的道理，只是构建顺序发生了变化，这里我就不一一实现了。

不过需要注意的是：

在中序遍历方法中，根节点位于遍历结果的中间位置。但是，中序遍历方法本身无法准确确定一棵树的根节点，因为没有足够的信息来区分子树的结构。

相比之下，前序遍历和后序遍历方法更适合构建树并确定根节点。在前序遍历中，根节点是遍历结果的第一个节点；而在后序遍历中，根节点是遍历结果的最后一个节点。

因此，如果只有中序遍历的遍历结果，我们很难确定树的根节点。为了准确确定根节点，需要同时获得一棵树的前序遍历或后序遍历结果，或者至少通过其他方式获得树的结构信息。

如果想要实现用后序遍历结果来构建树，方法如下：后序遍历的根节点是遍历结果的最后一个节点，构建顺序是先构建右子树，再构建左子树（构建的方法和前面的一样）并且数值也应该从后向前利用。

2）已知的遍历结果没有给出空树的位置

如果没有给出空树的位置，就不能只根据前序遍历和后序遍历构建树了，因为不能确定值是一个树的左子树还是右子树（空树是不打印的），例如：

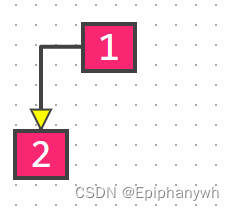
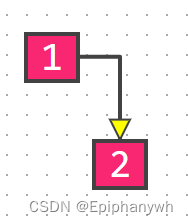
2分别是1的左右子树，但两种前序遍历打印出的结果是一样的，都是 12 .

所以，仅仅给出一个遍历结果是不能确定出一个树的，所以这种题型一般给出的条件都是两种遍历方式的结果，如下：

解这种题目的方法：

先来了解以下三种遍历方法的布局：

前序遍历：根节点+左子树+右子树

中序遍历：左子树+根节点+右子树

后序遍历：左子树+右子树+根节点

从结构可以看出：前序遍历/后序遍历容易得到根节点，中序遍历容易根据根节点得到左右子树的分布。

所以这种题型的解题方法就是：利用前后序遍历得到根节点，再利用根节点确定左右子树的布局，如果根节点的边有多个值时，需要在左边这些值中再一次确定根节点和左右子树的关系，直到树构建完成。

下面，我以上面这个题目为例，给出详细的解题步骤：

利用前序遍历得到根节点，利用中序遍历得到左右子树的数值分布。

利用前序遍历的结果找到根节点是5（其实选出这一题的答案非常容易：根节点是5，那么后序遍历结果最后一个值一定是5，选C），再根据中序遍历结果可以确定左右子树的数值分布：

（左子树）4 7 5 6 9 1 2（右子树）

对于左子树 4 7，也要用同样的方法确定根节点和左右子树的数值分布：

根据前序遍历结果：这两个数值的顺序是7 4 ，所以7是根节点，4是子树中的值；确定根节点后，再回到中序遍历的结果上 4 7 ，7是根节点，4在根节点的左面，所以4是左子树的值；在7的右面没有值，则说明右子树为空。所以，左子树的布局就得到了：

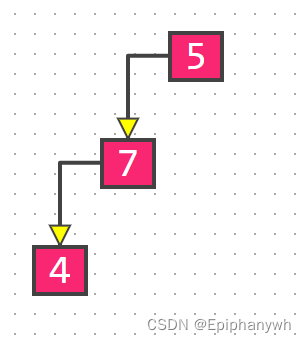
对于右子树 6 9 1 2，也要用同样的方法确定根节点和左右子树的数值分布：

根据前序遍历结果：这四个数值的顺序是9 6 1 2 ，所以9是根节点，6 1 2是子树中的值；确定根节点后，再回到中序遍历的结果上 6 9 1 2 ，9是根节点，6在根节点的左面，所以6是左子树的值；

在9的右面有 1 2 两个数，这就意味着1 2 也是根节点和子树的关系，再用同样的方法可以得到2是根节点，1是2的左子树，2的右子树为空。所以，右子树的布局就得到了：

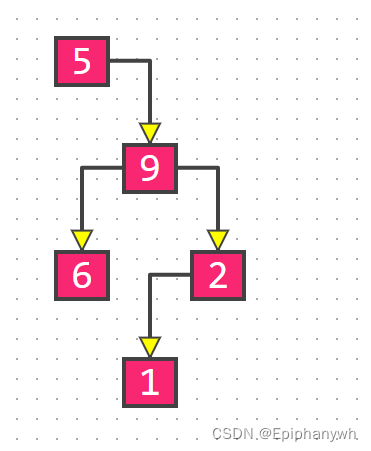
所以整棵树为：

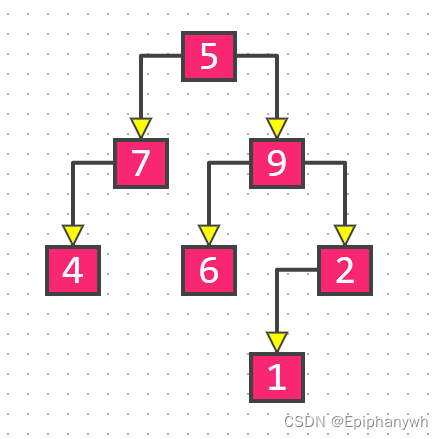
整棵树的布局都清楚了，那么得到后续遍历的结果就非常容易了。

当然题目给出的条件不一定都是前序遍历和中序遍历的结果，还可能是其他情况，如：

解题步骤：

利用后序遍历得到根节点，利用中序遍历得到左右子树的数值分布。

根据后序遍历可以得到根节点为A，再根据中序遍历确定左右子树数值的分布情况：

（左子树）JGDHKB A ELIMCF（右子树）

对于左子树 JGDHKB，也要用同样的方法确定根节点和左右子树的数值分布：

根据后序遍历结果：JGDHKB这几个字母的顺序是JGKHDB，所以B是根节点，JGKHD是子树中的值；确定根节点后，再回到中序遍历的结果上 JGDHKB ，B是根节点，JGKHD在根节点的左面，所以JGKHD是B左子树的值；在B的右面没有值，则说明右子树为空。

对于JGKHD而言，它们之间又是根节点和子树的关系，再用同样的方法得到具体布局。最后，左子树的布局就得到了：

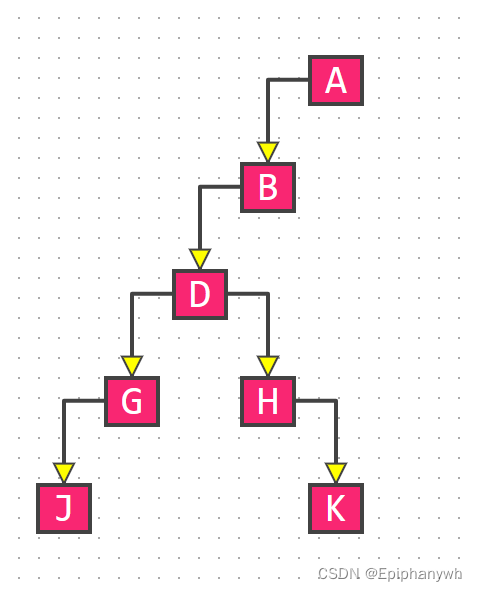
对于右子树也是同样的道理，我就不一一赘述了。

最后树的布局是：

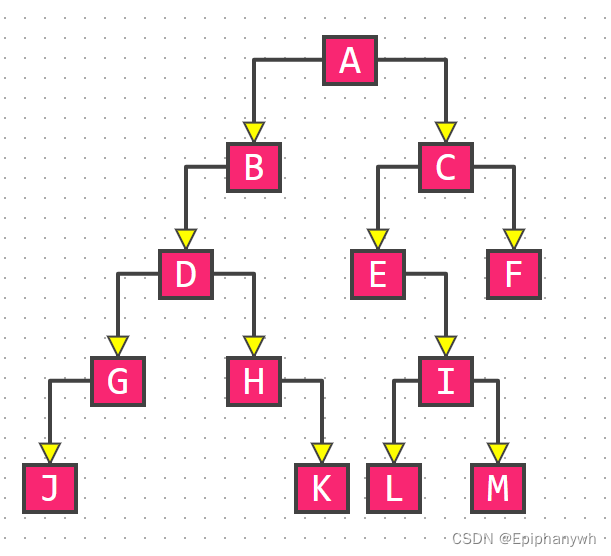
在这种题型中，大多是选择题，可以用上述方法实现；后面还需要用代码实现（题型三），这里我先不讲解，你先掌握第二种题型和第三种题型的前半段，对递归有一定了解后，再来看这一题会比较容易。

（二）求树节点个数/深度

1）树的节点总个数

递归思想：

总结点个数 = 左子树节点个数+右子树节点个数 + 1（根节点个数）

一次递归结束的条件：

将大问题拆分成最小的问题--当节点为空时，节点个数为0，返回0。

代码：

int TreeSize(BTNode* root)
{
	if (root == NULL)
		return 0;
	return TreeSize(root->left) + TreeSize(root->right) + 1;
}

2）树叶的节点个数

递归思想：

叶子结点个数 = 左子树叶子节点个数 + 右子树叶子节点个数

一次递归结束的条件：

将大问题拆分成最小的问题--当左子树并且右子树为空时，其根节点就是叶子节点，返回1；节点为空，无叶子节点，返回0。

代码：

int TreeLeafSize(BTNode* root)
{
	// 节点为空，返回0
	if (root == NULL)
	{
		return 0;
	}
	// 节点为叶子节点，返回1；
	if (root->right == NULL && root->left == NULL)
	{
		return 1;
	}
	// 其它，返回左节点+右节点
	return TreeLeafSize(root->right) + TreeLeafSize(root->left);
}

3）第K层节点个数

递归思想：

第K层的结点个数 = 左子树第 K-1 层的节点个数 + 右子树第 K-1 层的节点个数；

左子树第K-1层的节点个数 = 左子树第（k-1）-1层的节点个数 + 右子树第（k-1）-1层的节点个数……

一次递归结束的条件：

将大问题拆分成最小的问题--当K = 1时，找到第K层节点个数，返回1；节点为空，没有第K层节点个数，返回0。

代码：

int TreeKLevel(BTNode* root, int k)
{
	// 如果第K为NULL，返回0
	if (root == NULL)
		return 0;
	// 如果第K层不为NULL，返回1
	if (k == 1)
		return 1;
	// 如果是第K层以前的节点，左子树第 K-1 层的节点个数 + 右子树第 K-1 层的节点个数 
	return TreeKLevel(root->right, k - 1) + TreeKLevel(root->left, k - 1);
}

4）二叉树的最大深度

104. 二叉树的最大深度

二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。

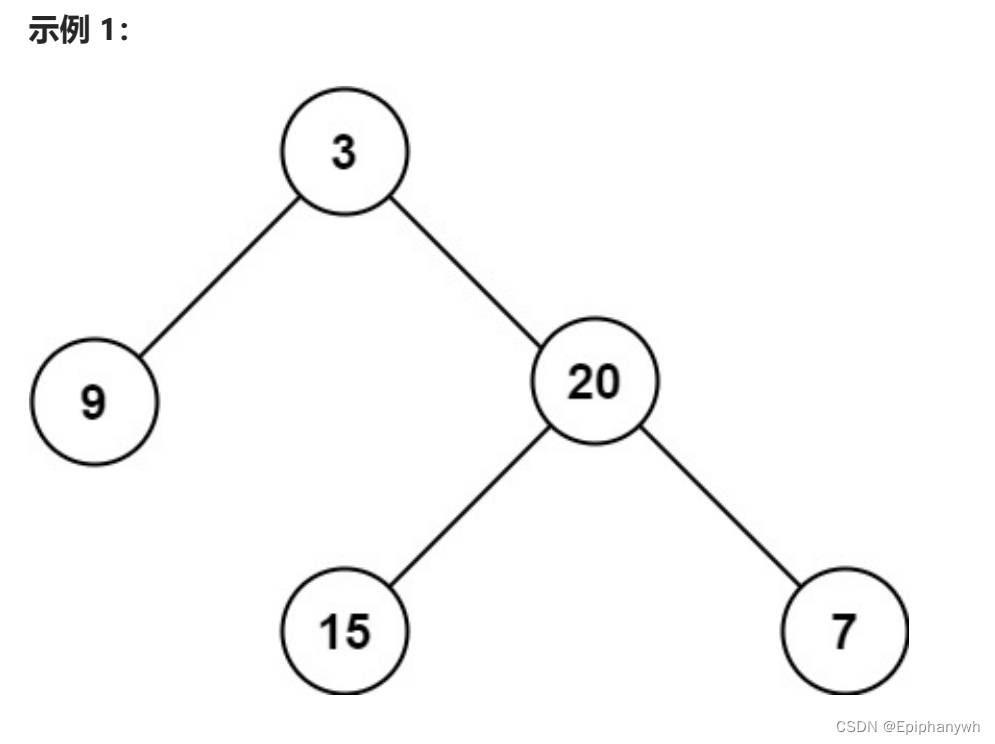
递归思想：

二叉树的深度 = 左子树的深度和右子树的深度中的较大值 + 1（根节点的深度）；

一次递归结束的条件：

将大问题拆分成最小的问题--节点为空，深度为0，返回0。

代码：

int maxDepth(struct TreeNode* root)
{

    // 如果节点为NULL，返回0
    if(root == NULL)
        return 0;
    int left_depth = maxDepth(root->left);
    int right_depth = maxDepth(root->right);
    return (left_depth > right_depth ? left_depth : right_depth) + 1;
    // return fmax(maxDepth(root->left), maxDepth(root->right))+1;

}

有的人代码可能会写成下面这种形式：

int maxDepth(struct TreeNode* root)
{

    // 如果节点为NULL，返回0
    if(root == NULL)
        return 0;
    
    return maxDepth(root->left)>maxDepth(root->right)?maxDepth(root->left)+1:maxDepth(root->right)+1;

}

这种方法也是可以解决问题的，但是有一个问题：左右子树深度会分别计算两次，效率比较慢。

这种方法第二次计算是不必要的，改进方法就是把前一次计算的结果记录下来（第一种方法）。

（三）二叉树的构建/遍历

注意这里的遍历，并不是我们在创建二叉树时将遍历结果直接打印出来，这里的遍历是将遍历结果存放的数组中。

1）前序遍历

在这里我就不说明前序遍历的思想了，主要说明一下需要注意的地方。

遍历的思想和遍历打印的思想是一样的，既然要将数组存放到数组中，就需要有一个数组，还要有下标。

易错点：

不过自己在写的时候，很可能出现下面这种错误写法


void PreOrder(struct TreeNode* root, int* a, int i)
{
    // 如果节点为空，就直接返回
    if(root == NULL)
        return;
    //节点不为空，将该节点存入数组中，并遍历其左右子树
    a[i++] = root->val;
    PreOrder(root->left, a, i);
    PreOrder(root->right, a, i);
}

这里a是一个数组，i是下标，下面我以这个树为例，看看能不能实现将前序遍历的结果存放到数组中：

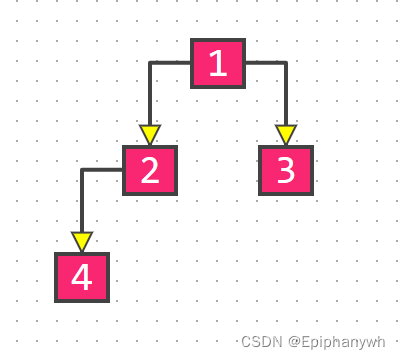
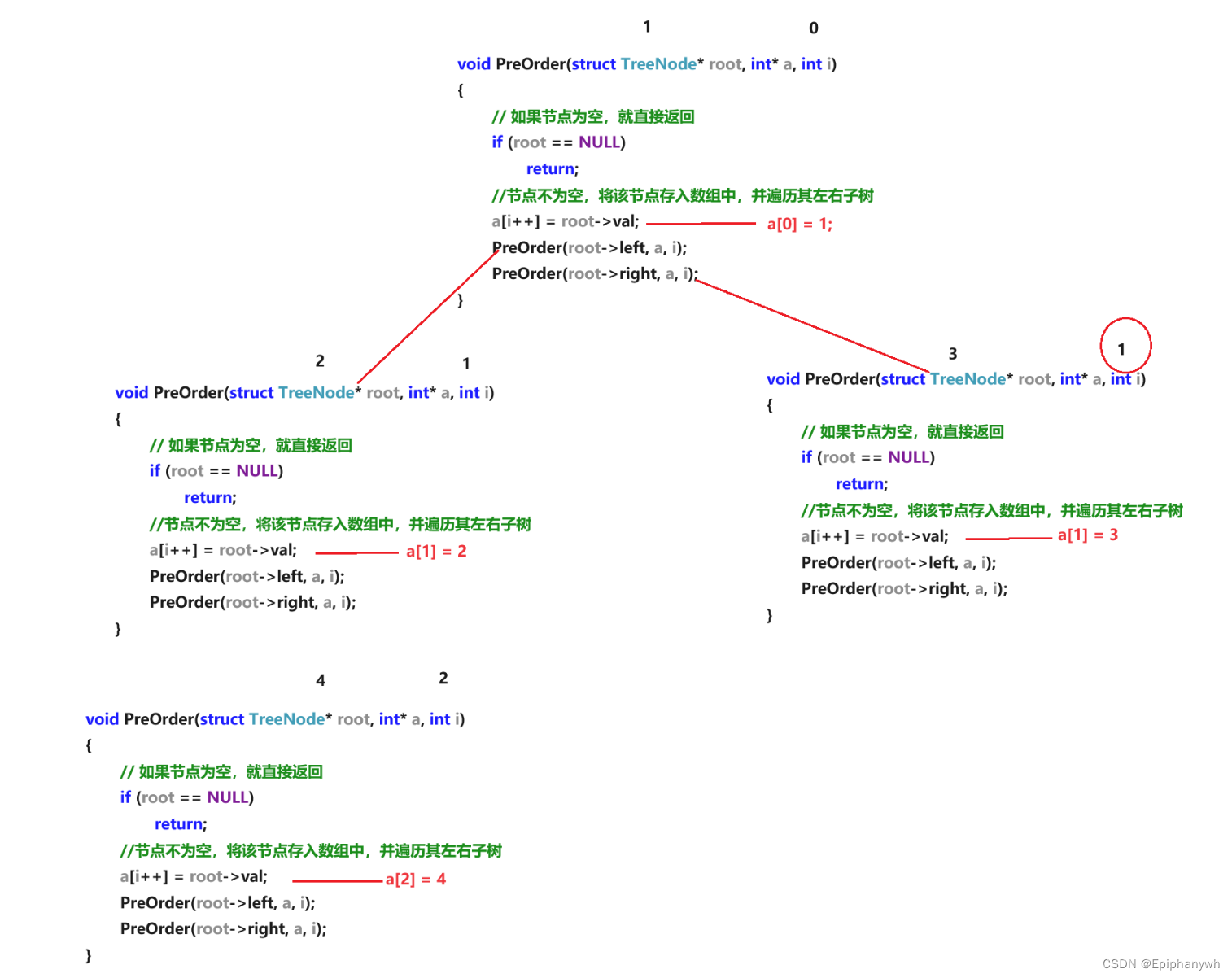
我们发现，再将3这个节点添加到数组中时，它的下标本应该是3，而实际下标是1。这是因为i是一个局部变量，每一个栈帧中的i都是孤立的，能够影响i的只有在进行下一次递归之前的栈帧。但是在左子树递归完成前是不会进行右子树的递归的，在左子树递归过程中，增加了下标，但是不能影响右子树的下标，所以就造成了错误。

因此应该用以下方法来解决本题：

// 参数i用指针，用作下标
void PreOrder(struct TreeNode* root, int* a, int* i)
{
    // 如果节点为空，就直接返回
    if(root == NULL)
        return;
    //节点不为空，将该节点存入数组中，并遍历其左右子树
    a[(*i)++] = root->val;
    PreOrder(root->left, a, i);
    PreOrder(root->right, a, i);
}

我们传递i的地址，这样在左子树递归过程中，增加了下标，右子树的下标也会同步的变化。

最终代码：

int TreeSize(struct TreeNode* root)
{
    // 如果节点为空，返回0
    if(root == NULL)
        return 0;
    // 如果节点不为空，个数加一，并计算其左右子树的节点个数
    return 1 + TreeSize(root->left) + TreeSize(root->right);
}

// 参数i用指针，用作下标
void PreOrder(struct TreeNode* root, int* a, int* i)
{
    // 如果节点为空，就直接返回
    if(root == NULL)
        return;
    //节点不为空，将该节点存入数组中，并遍历其左右子树
    a[(*i)++] = root->val;
    PreOrder(root->left, a, i);
    PreOrder(root->right, a, i);
}

 // 将前序遍历节点的值保存到数组中并返回数组
int* preorderTraversal(struct TreeNode* root, int* returnSize)
{
    // 可以先用一下计算节点个数的函数来确定开辟多大的空间
    int n = TreeSize(root);
    int* arr = (int*)malloc(sizeof(int)*n);
    *returnSize = n;
    // 遍历
    int i = 0;
    PreOrder(root, arr, &i);

    return arr;
}

其中TreeSize是用来计算树节点的个数，用来决定开辟数组空间的大小。

中序遍历和后序遍历的实现方法都是一致的，只是顺序发生了变化，我就不一一赘述了。

2）二叉树的构建和遍历

这里还有一种题目类型：先给你一种遍历类型，要求你构建出这棵树，并根据这棵树得到另一种遍历结果。（与第一种题目类型类似，不过这次要用代码实现）

二叉树遍历_牛客题霸_牛客网 (nowcoder.com)

（1）前序遍历构建树

首先需要根据先序遍历字符串用前序遍历的方法，构建出这棵树。

递归思想：

构建二叉树 = 构建根节点 + 构建左子树 + 构建右子树；

一次递归结束的条件：

将大问题拆分成最小的问题--如果数组的元素为空，构建的节点为空，返回NULL；如果不为空，构建根节点，继续构建左右子树。

同时又因为需要遍历数组获取节点的值，所以就需要下标，同样的道理，这里需要传递下标的地址。

代码：

typedef char BTDataType;

typedef struct BinaryTreeNode
{
	BTDataType data;
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
}BTNode;

BTNode* CreatTree(char* arr, int* pi)
{
    // 如果当前数组中的值为#，则该节点为NULL，就直接返回NULL
    if(arr[(*pi)] == '#')
    {
        (*pi)++;
        return NULL;
    }
    // 申请一个节点
    BTNode* root = (BTNode*)malloc(sizeof(BTNode));
    root->data = arr[*pi];
    (*pi)++;

    // 构建左右子树
    root->left = CreatTree(arr, pi);
    root->right = CreatTree(arr, pi);

    // 构建完成左右子树后，整棵树就构建完成了，返回根节点
    return root;
}

（2）中序遍历

// 中序遍历
void InOrder(BTNode* root)
{
    // 如果根节点为NULL，返回
    if(root == NULL)
        return;
    InOrder(root->left);
    printf("%c ", root->data);
    InOrder(root->right);
}

最终代码：

#include <stdio.h>
#include <stdlib.h>



typedef char BTDataType;

typedef struct BinaryTreeNode
{
	BTDataType data;
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
}BTNode;

BTNode* CreatTree(char* arr, int* pi)
{
    // 如果当前数组中的值为#，则该节点为NULL，就直接返回NULL
    if(arr[(*pi)] == '#')
    {
        (*pi)++;
        return NULL;
    }
    // 申请一个节点
    BTNode* root = (BTNode*)malloc(sizeof(BTNode));
    root->data = arr[*pi];
    (*pi)++;

    // 构建左右子树
    root->left = CreatTree(arr, pi);
    root->right = CreatTree(arr, pi);

    // 构建完成左右子树后，整棵树就构建完成了，返回根节点
    return root;
}


// 中序遍历
void InOrder(BTNode* root)
{
    // 如果根节点为NULL，返回
    if(root == NULL)
        return;
    InOrder(root->left);
    printf("%c ", root->data);
    InOrder(root->right);
}


int main() 
{
    char arr[100] = {0};
    scanf("%s", arr);
    // 利用前序遍历构建一颗二叉树
    int i = 0; // 下标
    BTNode* root = CreatTree(arr, &i);

    // 中序遍历
    InOrder(root);
    return 0;
}

（四）二叉树的特点

1）判断二叉树是否是满二叉树

递归思想：

判断整棵树是否是满二叉树 == 左子树和右子树是否是二叉树

一次递归结束的条件：

将大问题拆分成最小的问题--节点为空，返回真。

代码：

// 判断二叉树是否是满二叉树
int isFullBinaryTree(Node* root) {
    // 若为空树，则满足满二叉树的条件
    if (root == NULL) {
        return 1;
    }

    // 若左右子树不存在或者都存在，则继续递归判断
    if ((root->left == NULL && root->right != NULL) || (root->left != NULL && root->right == NULL)) {
        return 0;  // 左右子树不对称，不是满二叉树
    }

    // 递归检查左右子树是否满足满二叉树条件
    int left = isFullBinaryTree(root->left);
    int right = isFullBinaryTree(root->right);

    return left && right;
}

2）判断二叉树是否是完全二叉树

解题思路：

需要用到层序遍历的方法：

创建一个队列，并将根节点入队。
循环执行以下步骤，直到队列为空： a. 出队一个节点，并访问该节点。 b. 如果该节点有左子节点，则将左子节点入队。 c. 如果该节点有右子节点，则将右子节点入队。
遍历完所有节点后，遍历过程结束

不过用队列解决这个题目，需要将步骤改动一下：

创建一个队列，并将根节点入队。
a. 出队一个节点，并访问该节点。 b. 如果该节点的左子节点为空，也应该将左子节点入队。 c. 如果该节点的右子节点为空，也应该将右子节点入队。d. 出对头后，判断对头是否为空：如果为空，退出循环，如果不为空，继续。
循环步骤二，直到循环结束。循环结束后，检查队列中还有没有不为空的队列元素：如果没有，则说明该树是完全二叉树；如果还有，则说明该树不是完全二叉树。

代码：

bool BinaryTreeComplete(BTNode* root)
{
	//创建一个队列并初始化
	Queue q;
	QueueInit(&q);
	// 将根节点队列
	if (root)
		QueuePush(&q, root);
	while (!QueueEmpty(&q))
	{
		struct BinaryTreeNode* temp = QueueFront(&q);
		// 如果出队的节点为NULL，就退出循环，进行判断
		if (temp == NULL)
			break;
		// 将下一层入队，节点为空也要入队
		QueuePush(&q, temp->left);
		QueuePush(&q, temp->right);
		//删除对头
		QueuePop(&q);
	}
	// 判断
	while (!QueueEmpty(&q))
	{
		struct BinaryTreeNode* Node = QueueFront(&q);
		if (Node != NULL)
		{
			QueueDestroy(&q);
			return false;
		}
		QueuePop(&q);
	}

	//销毁队列
	QueueDestroy(&q);
	return true;
}

3）判断二叉树是否是对称二叉树

101. 对称二叉树

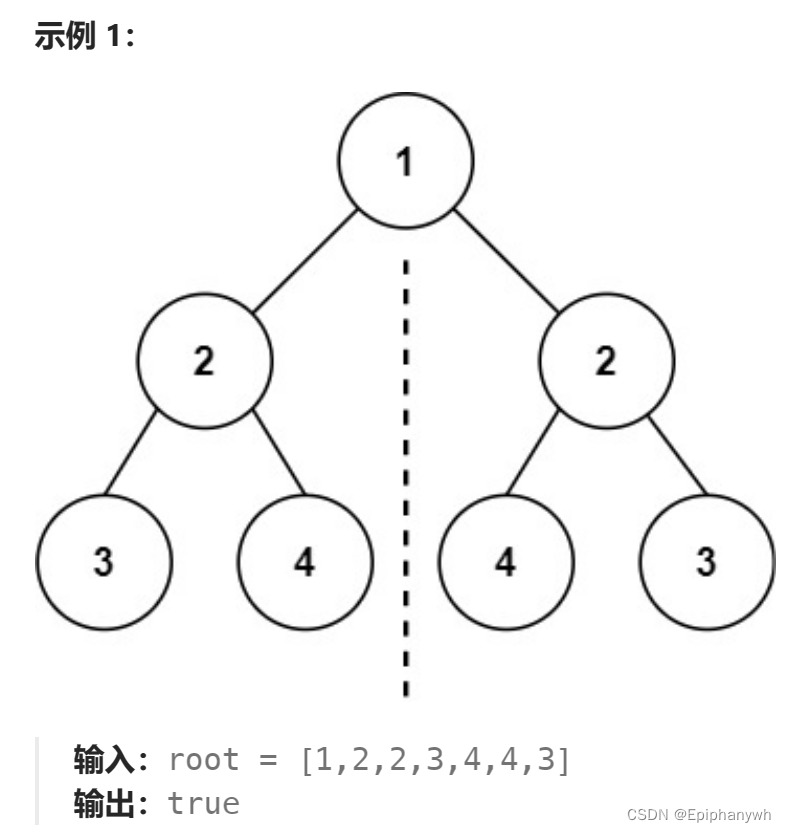
递归思想：

整棵树的对称性与根节点1没有关系（整棵树的根节点），主要是左右子树的关系和左右子树根节点的值决定整棵树的对称性：

如果左右子树对称，则整棵树就是对称的。左右子树是否对称需要判断根节点是否相等、左子树的左右子树与右子树的左右子树的关系是否对称……

一次递归结束的条件：

将大问题拆分成最小的问题--

左子树为空并且右子树为空，则树是对称的，返回真；

左子树为空，右子树不为空（左子树不为空，右子树为空），则左右不对称，返回假；

左子树和右子树根节点的值不相等，则左右不对称，返回假；

代码：

bool isSymmetricHelper(struct TreeNode* left, struct TreeNode* right) {
    if (left == NULL && right == NULL) {
        return true;
    }
    if (left == NULL || right == NULL) 
    {
        return false;
    }
    if (left->val != right->val) {
        return false;
    }
    return isSymmetricHelper(left->left, right->right) &&
           isSymmetricHelper(left->right, right->left);
}

bool isSymmetric(struct TreeNode* root) {
    if (root == NULL) {
        return true;
    }
    return isSymmetricHelper(root->left, root->right);
}

4）翻转二叉树

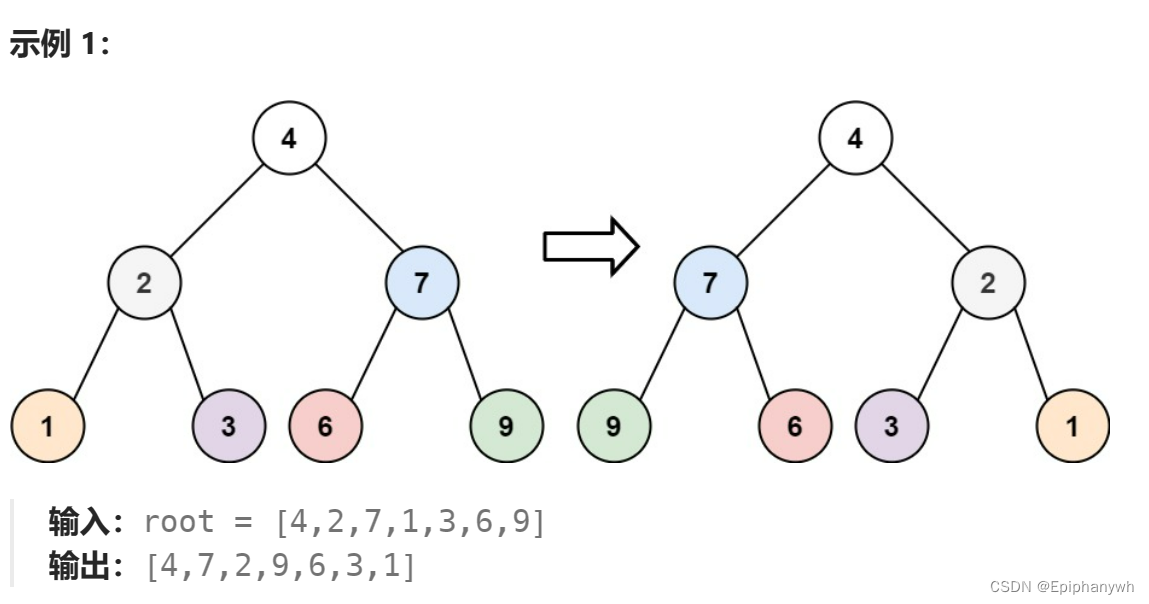
递归思想：

翻转整棵树 = 翻转根节点的左右子树；

翻转左右子树 = 翻转左右子树的左右子树……

一次递归结束的条件：

将大问题拆分成最小的问题--

如果节点为空，返回NULL；

代码：

struct TreeNode* invertTree(struct TreeNode* root)
{
    if (root == NULL) 
    {
        return NULL;
    }
    struct TreeNode* left = invertTree(root->left);
    struct TreeNode* right = invertTree(root->right);
    root->left = right;
    root->right = left;
    return root;
}

（五）两棵树的关系

1）两棵树是否相同

其实这题的代码逻辑和前面判断二叉树是否是对称二叉树的逻辑是一样的。不过也略有差异。

相同的树

给你两棵二叉树的根节点 p 和 q ，编写一个函数来检验这两棵树是否相同。

如果两个树在结构上相同，并且节点具有相同的值，则认为它们是相同的。

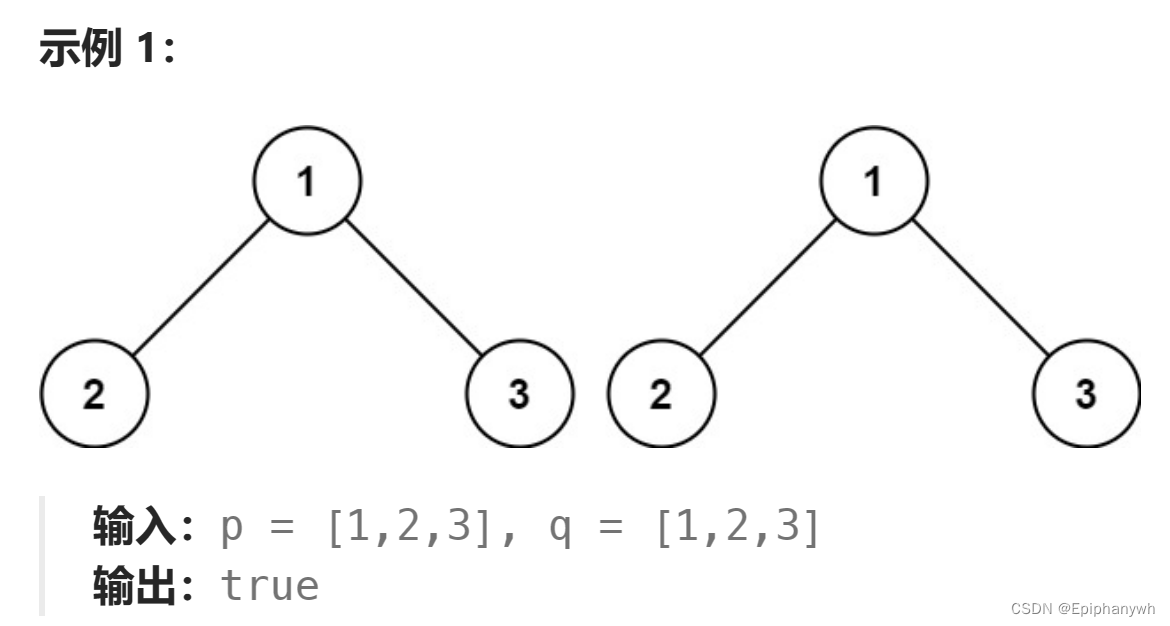
递归思想：

两棵树相等 = 两棵树根节点相等 + 两棵树的左右子树相等；

两棵树的左子树（右子树）相等 = 两棵树根节点相等 + 两棵树的左右子树相等……

一次递归结束的条件：

将大问题拆分成最小的问题--

左子树为空并且右子树为空，则树是相等的，返回真；

左子树为空，右子树不为空（左子树不为空，右子树为空），则左右不相等，返回假；

左子树和右子树根节点的值不相等，则左右不相等，返回假；

代码：

bool isSameTree(struct TreeNode* p, struct TreeNode* q)
{
    // 如果两颗子树节点都等于NULL，返回true
    if(p == NULL && q == NULL)
        return true;

    // 如果两个树中，有一个节点为空就说明节点不相等，就返回false(避免对NULL的解引用)
    if(p == NULL || q == NULL)
    {
        return false;
    }
    
    // 如果节点的值不相等，就返回false
    if(p->val != q->val)
    {
        return false;
    }

    // 如果两节点的值相等，就判断其左右子树是否全部相等
    return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
}

2）判断是否是子树关系

572. 另一棵树的子树

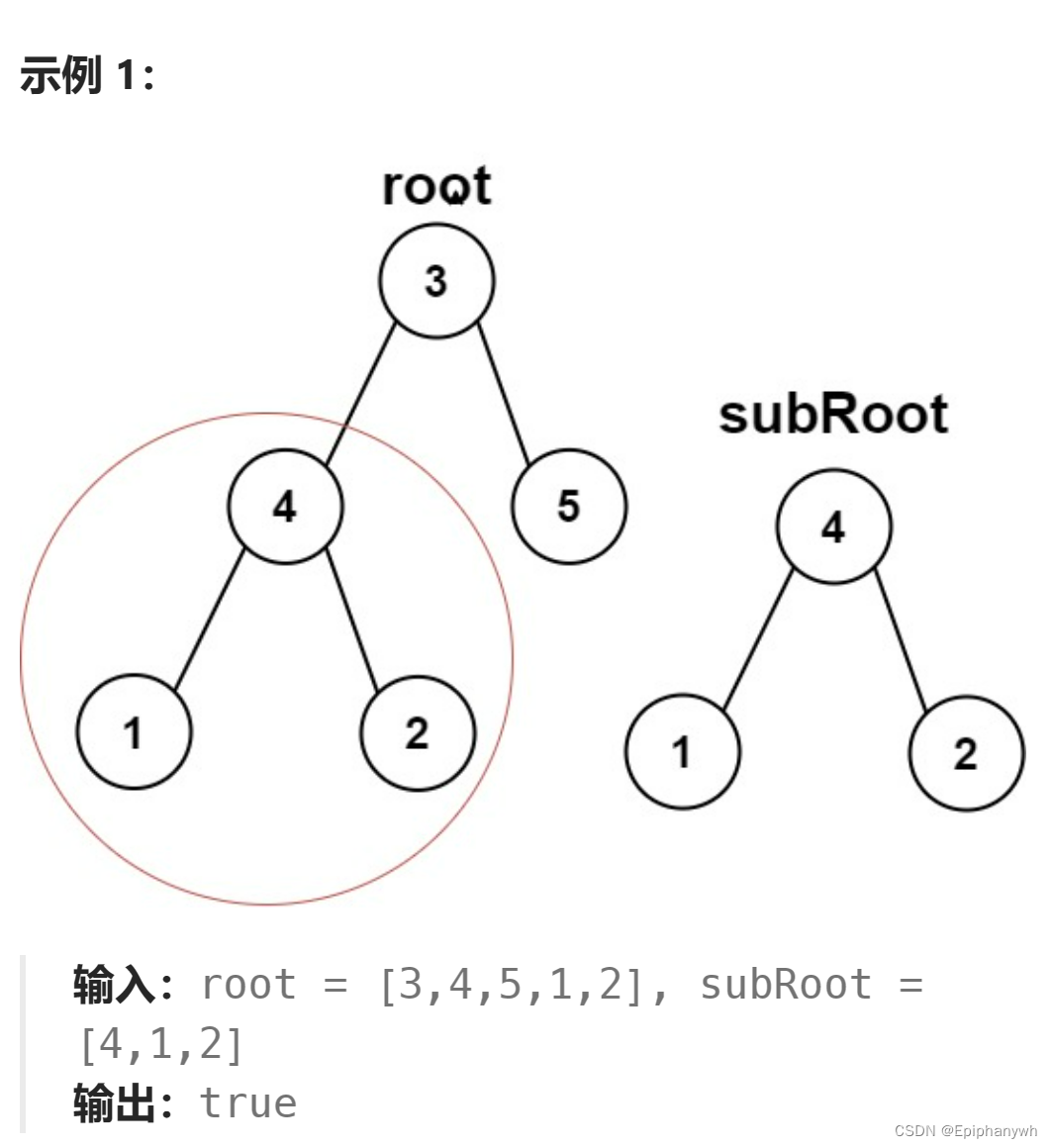
给你两棵二叉树 root 和 subRoot 。检验 root 中是否包含和 subRoot 具有相同结构和节点值的子树。如果存在，返回 true ；否则，返回 false 。

二叉树 tree 的一棵子树包括 tree 的某个节点和这个节点的所有后代节点。tree 也可以看做它自身的一棵子树。

递归思想：

判断两棵树的根节点是否相等：如果相等，就判断两棵树是否相等：如果相等，一方就是子树关系；

如果根节点不相等/两棵树不相等，判断大树的左子树与小树是否相等；判断大树的右子树与小树是否相等；-- 如果左子树和右子树有一边与小树相等，一方就是子树关系；

如果节点为空，则没有找到相等的树，返回false；

代码：

bool isSameTree(struct TreeNode* p, struct TreeNode* q)
{
    // 如果两颗子树节点都等于NULL，返回true
    if(p == NULL && q == NULL)
        return true;

    // 如果两个树中，有一个节点为空就说明节点不相等，就返回false(避免对NULL的解引用)
    if(p == NULL || q == NULL)
    {
        return false;
    }
    
    // 如果节点的值不相等，就返回false
    if(p->val != q->val)
    {
        return false;
    }

    // 如果两节点的值相等，就判断其左右子树是否全部相等
    return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
}

bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot)
{
    // 如果节点值为空，就返回false
    if(root == NULL)
        return false;

    // 如果节点值相等，就判断两棵树是否相等
    if(root->val == subRoot->val)
    {
        // 如果相等，就返回true
        if(isSameTree(root, subRoot))
            return true;
        // 如果不相等，继续判断下一个子树
    }
    // 如果节点值不相等，判断其左右子树是否有一个与子树相等：如果有一个相等，返回true；两个都不相等，返回false
    return isSubtree(root->left, subRoot) || isSubtree(root->right, subRoot);
}

今天的分享就到这里了，如果，你感觉这篇博客对你有帮助的话，就点个赞吧！感谢感谢……

Epiphanywh

关注

7
点赞
踩
3

收藏

觉得还不错? 一键收藏
4
评论
二叉树OJ

这种题型给出的条件一般是以下形式（其中#代表空格，下面我为了方便，我将给出的条件整体用一个数组描述）：假设给出的条件是用前序遍历获得的结果，由此构建原先树的思想如下：先来说一下构建树的递归思想，例如构建下面这棵树：将构建整棵树拆分成若干个小问题：整棵树是由根节点1和左右子树组成的，而左子树也是由根节点2和左右子树组成的，右子树也是由根节点3和其左右子树构成的。又因为整棵树最小可以拆分成以4为根节点的树：它的左子树是空，这也就意味着左边不会再向下构建子树了（4的左子树构建完成）；
复制链接

扫一扫