算法空间复杂度变化的主因包括:存储与问题规模相关变量的内存开销,
以及函数调用(如递归)带来的额外内存开销。
 ### 递归函数
### 递归函数 loveYou 内存开销分析
-
函数定义:
- 函数
void loveYou(int n)中,n为问题规模。函数内声明了三个局部变量a、b、c,这些变量所占空间大小为常量。
- 函数
-
递归调用逻辑:
- 当参数
n > 1时,函数会递归调用自身,传入参数为n - 1。 - 例如在
main函数中调用loveYou(5),会开启递归过程。
- 当参数
-
递归调用的内存过程:
- 程序代码装入:程序运行前,将程序代码放入内存,这部分空间大小固定,与问题规模无关。

-
逐层调用(接下来在main函数里调用love You()):
- 第一层调用
loveYou(5),函数运行声明变量a、b、c,需在内存中开辟空间存储参数n(值为 5 )和变量a、b、c。(和我们之前分析的那些函数一样也需要把这个函数运行过程中所涉及到的这些参数和变量存放到内存里) - 由于
n = 5 > 1,进行第二层调用loveYou(4),(然后它里边有a、b、c这几个变量。在第二层调用中n=4,虽然它们都叫n,但是在内存当中其实是两份不一样的数据,同时,在第二层调用当中,它也会有a、b、c这几个变量。同样,虽然名字和上面这个看起来一样,但其实在内存当中,这几个变量都是存放在不同的区域。)同样要在内存中开辟新空间存储参数n(值为 4 )和新声明的变量a、b、c。尽管变量名相同,但在内存中是不同区域(所以这次函数调用相关的这些参数和变量,同样也需要在内存当中开辟一片空间来存放这些数据。)。 - 依此类推(再往后的几层调用同样如此,每一层的调用都需要把这层调用中的参数n、
和局部变量a、b、c用一片专门的内存空间用于存储),直到第五层调用loveYou(1),此时n = 1,不满足if(n > 1)条件,(这次调用会直接跳过这个if语句)直接执行printf("I Love You %d\n", n);语句 。

- 第一层调用
-
逐层返回:当第五层调用结束,这一层函数相关信息数据从内存删除。然后逐层返回,系统根据内存保存信息恢复函数执行环境。 (具体用到函数调用栈
暂不展开)
-
空间复杂度分析:
假设变量n、a、b、c总共占 16 个字节(在 loveYou 函数递归调用示例中,变量 n 和 a、b、c 所占空间固定共约 16 字节,可简单认为每层函数调用需 16 字节存信息,实际实际还包含函数返回地址等信息,此处未作详细展开),即每一层函数调用需k(常数)字节空间。当n = 5时,递归调用五层,递归调用层数与问题规模n相等,所以问题规模为n时,所需内存空间大小为kn字节,用大O表示法,空间复杂度为O(n)。
请添加图片描述
在考研中, 多数递归相关空间复杂度分析类似,空间复杂度常等于递归调用的深度。
返回之后就可以把这层函数相关的这一些信息数据给删除了。
当返回到这一层的时候,系统会根据内存当中保存的这些信息来恢复这个函数相应的执行环境。
。
递归函数空间复杂度特殊情况分析
-
常规递归空间复杂度情况:多数递归相关空间复杂度分析中,空间复杂度等于递归调用深度。因为每一层递归调用所需内存空间大小为常量
k字节,例如之前简单递归示例中,各层存储固定的参数和局部变量等信息。

-
特殊递归示例(每一层的递归都会定义一个int型的数组):
- 函数定义与递归逻辑:以
loveYou函数为例,函数void loveYou(int n)中,当n > 1时递归调用自身。与之前不同的是,函数内声明了长度与n相关的int型数组flag[n](这个数组的长度和这一级递归的参数n是相同的)。 - 内存空间变化:
- 第一层调用
loveYou(5)时(n=5),数组flag长度为 5 ;第二层调用loveYou(4)(n=4),数组flag长度为 4 ,依此类推,第n级调用数组长度为n。 - 每一级函数调用中,用于存放数组等变量的空间大小不同,不再是固定常量。
- 在递归调用中,每一层创建的数组长度等于当前传入的参数
n。具体来说:
- 第一层调用
- 函数定义与递归逻辑:以
- 第一层调用时
n=5,数组长度为 5; - 第二层调用时
n=4,数组长度为 4; - 第三层调用时
n=3,数组长度为 3; - 依此类推,第
k层调用时数组长度为k,直到第n层调用时数组长度为n。- 空间复杂度计算:由于声明的这个数组长度与这一级调用所传入的参数n有关,故各级函数调用存放变量所需空间大小不同。各级递归调用存储
flag数组的空间大小构成首项为 1 、末项为n、项数为n的等差数列。根据等差数列求和公式
- 空间复杂度计算:由于声明的这个数组长度与这一级调用所传入的参数n有关,故各级函数调用存放变量所需空间大小不同。各级递归调用存储
- 考研相关情况:考研中绝大多数递归程序空间复杂度类似常规情况,即等于递归调用深度;此类复杂情况(如数组长度与
n相关的递归 )较少遇到。
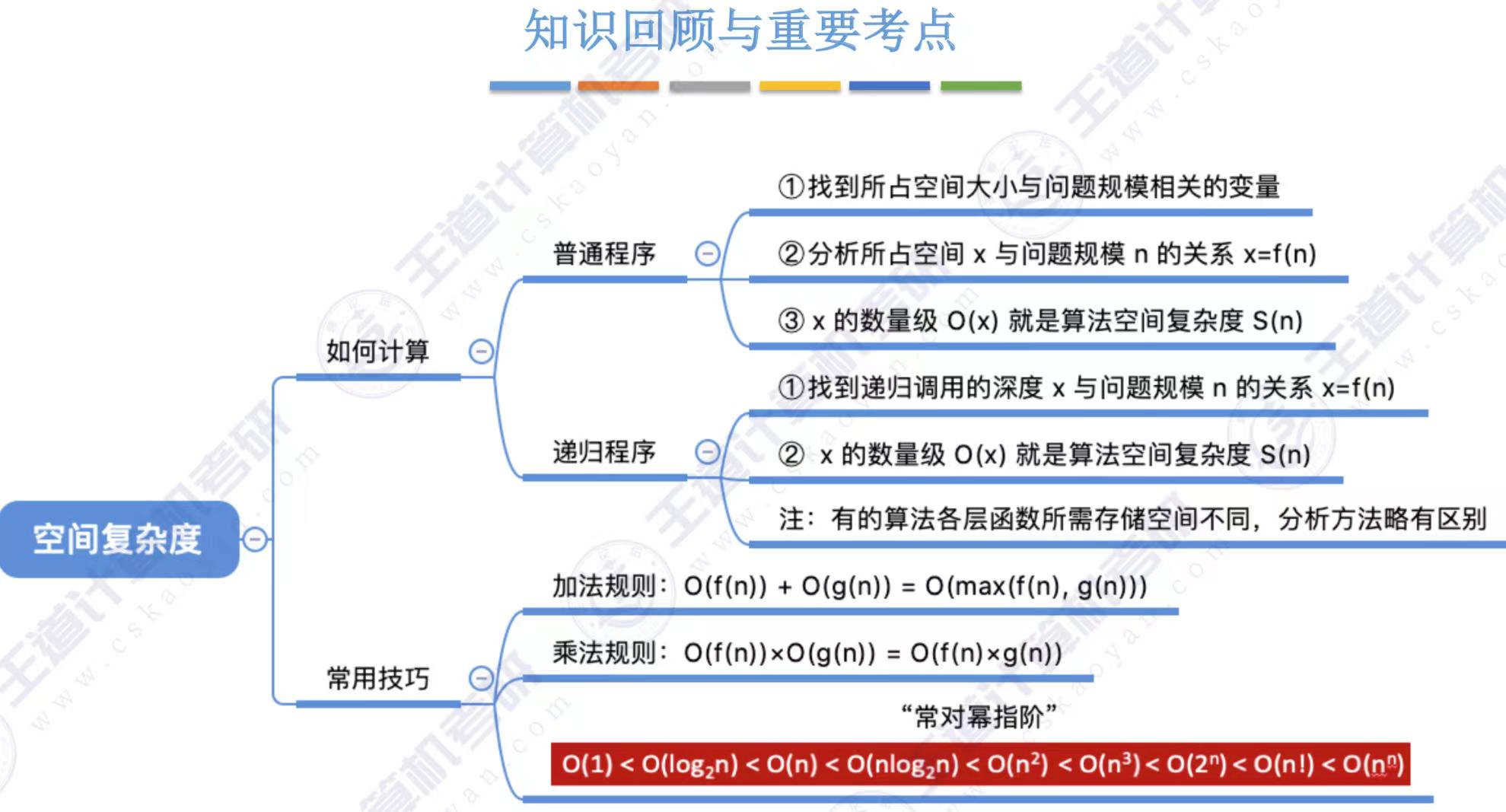
算法空间复杂度学习总结
在本小节,我们学习了算法空间复杂度的计算方法。考研中,可能涉及普通程序或递归程序空间复杂度的分析。
普通程序空间复杂度分析
- 分析相对简便。找出与问题规模
n相关的变量,探究这些变量所占空间大小与问题规模n的关联。 - 采用大
O表示法表示空间复杂度,关注数量级。实际分析中,无需纠结变量具体字节数,大O表示法只看数量级,舍去系数。
递归程序空间复杂度分析
- 分析相对困难。考研里,多数递归程序只需关注递归调用深度与问题规模
n的关系。 - 调用深度
x的数量级通常就是其空间复杂度。计算空间复杂度时,大O表示法运算技巧与时间复杂度通用。
考研考察侧重
总体而言,考研中时间复杂度考察更频繁,空间复杂度考察较少。后续学习众多算法时,还会继续剖析空间复杂度,会有更多实践机会。
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








