算法基础课——搜索与图论
导论
- 深度优先搜索 DFS
- 宽度优先搜索 BFS
- 树与图的深度优先遍历
- 树与图的宽度优先遍历
- 拓扑排序
- 最小生成树
- 二分图
知识点
- DFS和BFS都可以对我们整个空间进行遍历。搜索的结构都是像一棵树一样,但是搜索的顺序是不一样的。
- DFS每一次只搜索一条路,一条路走到黑,搜索到叶节点的时候会进行回溯,也就是一条路会走到头,回溯也不会直接回到最开始的点
- BFS是同时搜索很多条路,也就是一层层搜索
- 数据结构DFS→stack(记录这一条路上的点)→ O(n), BFS→queue(每一层的点)→O(n^2)。DFS所用的空间比BFS有绝对优势。当所有边的权重是1的时候,BFS搜到的点一定是符合条件的最近的点→最短路
- 问最短、几次→BFS;比较奇怪,对空间要求高→DFS
- DP问题和最短问题是互通的。DP问题可以看成一个特殊的最短路问题,是没有环存在的最短路问题。
有向图存储:邻接矩阵、邻接表
-
有向无环图才有拓扑序列。
// 伪代码,queue<- 所有入度为0的点 while queue 不为空 { t <- 队头 枚举t的所有出清除t->j 删除t->j,d[j] -- if (d[j] == 0) { j入队 } } -
最短路问题:分成两大类,单源最短路(一个点到其他所有点的最短距离)和多源汇最短路(多个点到多个点的最短距离,起点和终点都是不确定的)
源点→起点,汇点→终点
单源最短路还可以细分:所有边权都是正数(朴素Dijkstra,堆优化的Dijkstra算法);存在负权边
约定:n是代表点数,m代表边数

我们发现朴素版的Dijkstra和边数没有关系。稠密图(边多)尽量使用朴素版的Dijkstra,稀疏图用堆优化的Dijkstra算法
SPFA一般是规定不超过k条边的时候。Bellman-Ford算法是少数情况用。
最短路问题的考察侧重点是怎么 建图,怎么把边和点从题目中抽象出来。
朴素版的Dijkstra算法
s:当前已经确定最短距离的点 1. 初始化距离 dist[1] = 0.dist[v] = +无穷 2. for i : 1~n 1. t ← 不在s中的最短距离的点 2. s←t 3. 用t更新其他点的距离(从t能直接到的点,能不能更新,即dist[x] > dist[i] + t)#include <iostream> #include <cstring> #include <algorithm> using namespace std; const int N = 500 + 10; int n, m, res; bool state[N]; int dist[N], g[N][N]; // int dij(int n, int dist[], int g[][]) int dij() // 全局变量不需要传参数 { for (int i = 1; i < n; i ++ ) { int t = -1; for (int j = 1; j <= n; j ++ ) { if( !state[j] && (t == -1 || dist[t] > dist[j])) t = j; // 第一次没有写 t == -1 的条件,导致循环结束以后数组的下标超出范围 // 找出还没有加入“已经是最短距离”的集合中的距离最短的点 } state[t] = true;// 修改状态 for (int j = 1; j <= n; j ++ ) { dist[j] = min(dist[j], dist[t]+g[t][j]); } } if(dist[n] == 0x3f3f3f3f) return -1; return dist[n]; } int main() { cin >> n >> m; memset(g, 0x3f, sizeof g); while (m -- ) { int a, b, c; cin >> a >> b >> c; g[a][b] = min(g[a][b], c); } memset(dist, 0x3f, sizeof dist);// 最短路径,初始化 dist[1] = 0; // 1到1的距离为0 int res = dij(); cout << res << endl; return 0; }堆优化的Dijkstra
不使用手写堆,直接用优先队列。
稀疏图→邻接表, 稠密图 →邻接矩阵
// 堆优化的Dijkstra算法 #include <iostream> #include <cstring> #include <algorithm> #include <queue> using namespace std; const int N = 150010; typedef pair<int, int> PII; // 由于是稀疏图用链表保存 int e[N], ne[N], h[N], idx; int w[N]; // 保存每条边的权重 bool st[N]; // 用于保存每一个点是否知道1到此点的最短距离 int dis[N]; int n ,m; void add(int x, int y, int z) { e[idx] = y, ne[idx] = h[x], w[idx] = z, h[x] = idx ++; } int dijkstra() // 求1号点到n号点的最短路距离,如果从1号点无法走到n号点则返回-1 { // 定义一个小根堆 priority_queue<PII, vector<PII>, greater<PII>> heap; memset(dis, 0x3f, sizeof dis); dis[1] = 0; // 到第一个点的距离是0 // 放入优先队列里 heap.push({0, 1}); while(heap.size()) { // int t = heap.top(); // 这样会在heap.top这里报错 // 取出优先级队列里最小的那个 auto t = heap.top(); heap.pop(); // 点的名字和1到该点的距离 int point = t.second, d = t.first; // 如果是已经达到距离1最小则跳过这次 if(st[point]) continue; // 更新,这一次对其他进行更新之后,该点也可以以后跳过了,因为其也到达最小距离了 st[point] = true; for (int i = h[point]; i != -1; i = ne[i] ) { int j = e[i]; // if(dis[j] > d + w[j]) // 是用 i去更新…… if(dis[j] > d + w[i]) { dis[j] = d + w[i]; heap.push({dis[j], j}); } } } if(dis[n] == 0x3f3f3f3f) return -1; return dis[n]; } int main() { cin >> n >> m; // 初始化 memset(h, -1, sizeof h); while (m -- ) { int x, y, z; cin >> x >> y >> z; add(x, y, z); } int res = dijkstra(); cout << res; return 0; }Bellman-Ford算法
for n次 // 备份 for所有边 a, b, w (a->b的边,权重是w) // 松弛操作 // 存边方式比较简单,就是定义一个结构体对abw直接进行保存 // 注意!需要先备份一次, // 因为我们只能用上一次迭代的结果对dist数组进行更新 //否则可能会使dist的更细突破了n的数值的限制 dist[b] = min(dist[b], dist[a] + w)两个for循环之后,dist[b] 小于等于 dist[a] + w 三角不等式
不一定能找到最短距离,如果存在负权回路的话。当然存在回路也不一定不存在最短距离。比如:

这个环不在1→2的路径上。
假如说迭代了k次,当前的dist的意思是从1开始经过不超过k条边到各个点的最短距离。当第n次迭代的时候,dist数组依旧有更新,就说明1→2→……→x最多有n+1个点,根据抽屉原理可知有至少有两个点是同一个点,即存在环!
一般来说SPFA算法要优于Bellman-Ford算法,但是有些情况只能使用Bellman-Ford算法,比如说当我们规定了要经过边数不超过k条找到最短路径。使用SPFA就一定不能含有赋环。
// bellman_ford #include <iostream> #include <cstring> #include <algorithm> using namespace std; const int N = 10010; int n, m, k; int dis[N]; int backup[N]; struct Edge { int a, b, w; }edge[N]; void bellman_ford() { memset(dis, 0x3f, sizeof dis); // 第一次忘记初始化第一个数字了…… dis[1] = 0; for (int i = 0; i < k; i ++ ) { memcpy(backup, dis, sizeof backup); for (int j = 0; j < m; j ++ ) { int a = edge[j].a, b = edge[j].b, w = edge[j].w; // dis[b] = min(dis[b], dis[a] + w); // 不能用修改之后的进行更新…… dis[b] = min(dis[b], backup[a] + w); // cout << dis[1] << " " << dis[2] << " " << dis[3] << endl; // if(dis[b] > dis[a] + w ) // { // dis[b] = backup[a] + w; // } } } } int main() { cin >> n >> m >> k; for (int i = 0; i < m; i ++ ) { int a, b, w; cin >> a >> b >> w; edge[i].a = a; edge[i].b = b; edge[i].w = w; } bellman_ford(); if(dis[n] > 0x3f3f3f3f/2) puts("impossible"); else cout << dis[n]; // cout << res; return 0; }SPFA
其实是对Ford算法做一个优化。用宽搜做优化。
更新的时候是dist[b] = min(dist[b], dist[a] + w),只有dist[a]变小了,dist[b]才能变小,所以我们针对这里做优化。
用一个队列记录所有变小的dist[a]
queue <- 1 while queue is not empty 1. t <- q.front q.pop(); 2. 更新t的所有出边 t->b queue <- b // 因为b更新了,所以又要加入队列, // 如果b已经在里面了,就要判断一下不要加入有很多正权图的问题也可以用SPFA过掉,如果SPFA被卡了,就换其他算法。·
一般不用Bellman-Ford算法判定负权环,一般用SPFA。(如果出题人阴险,就会卡SPFA)
怎么求负环,也是应用抽屉原理:
用一个cnt数组,假如有cnt >= n,则说明有环,即有负环。 如果出现cnt[x] >= n则马上返回true// spfa求1到n的最短距离 #include <iostream> #include <cstring> #include <algorithm> #include <queue> using namespace std; const int N = 100010; int n,m; int h[N], e[N], ne[N], w[N], idx; bool st[N]; int dist[N]; void add(int a, int b, int c) { e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx ++; } void spfa() { queue<int> q; memset(dist, 0x3f, sizeof dist); dist[1] = 0; q.push(1); st[1] = true; while(q.size()) { int t = q.front(); q.pop(); st[t] = false; for (int i = h[t]; i != -1; i = ne[i] ) { int j = e[i]; if(dist[j] > dist[t] + w[i]) // 是dist[t],而不是dist[i],t才是模板中的a { dist[j] = dist[t] + w[i]; if(!st[j]) { q.push(j); st[j] = true; } } } } // cout << dist[n] << endl; if(dist[n] == 0x3f3f3f3f) cout << "impossible" << endl; else cout << dist[n] << endl; } int main() { cin >> n >> m; memset(h ,-1, sizeof h); while (m -- ) { int a, b, c; cin >> a >> b >> c; add(a, b, c); } spfa(); return 0; }// spfa判断负环 #include <iostream> #include <cstring> #include <algorithm> #include <queue> using namespace std; const int N = 10010; int n, m; int h[N], e[N], ne[N], w[N], idx; int cnt[N]; bool st[N]; int dist[N]; queue<int> q; void add(int a, int b, int c) { e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx ++; } bool spfa() { // memset(dist, 0x3f, sizeof dist); // dist[1] = 0; // q.push(1); // st[1] = true; for (int i = 1; i <= n; i ++ ) { st[i] = true; q.push(i); // 需要把所有点放到里面,因为从1开始不一定能走到那个负环 } while(q.size()) { int t = q.front(); q.pop(); st[t] = false; for (int i = h[t]; i != -1; i = ne[i]) { int j = e[i]; if(dist[j] > dist[t] + w[i]) { dist[j] = dist[t] + w[i]; cnt[j] = cnt[t] + 1; if(cnt[j] >= n) { return true; } if(!st[j]) { q.push(j); st[j] = true; } } } } return false; } int main() { cin >> n >> m; // 记得初始化…… memset(h, -1, sizeof h); while (m -- ) { int a, b, c; cin >> a >> b >> c; add(a, b, c); } bool res = spfa(); if(res) puts("Yes"); else puts("No"); return 0; }Floyd
d[i,j] = 存储所有的边 for (k = 1; k <= n; k ++) for (i = 1; i <= n; i ++) for (j = 1; j <= n; j ++) d[i, j] = min(d[i,j], d[i, k] + d[k, j])
无向图
一般都是无向图。稠密图直接用朴素版的Prim算法,稀疏图用Kruskal算法。
朴素版Prim算法→生成树
和Dijkstra算法很相似。
dist[i] <- +00
// 需要加入n个点,所以迭代n次
for (i = 0; i < n; i ++)
1. t <- 找到集合外距离最近的点
2. 用t更新其他点到集合的距离 // Dijkstra是更新到起点的距离
//什么叫某个点到集合的距离:看该点要连接到该集合有多少条边,我们 选择最短的那条
堆优化的Prim
不使用手写堆,直接用优先队列。
稀疏图→邻接表, 稠密图 →邻接矩阵
查找:O(1)*n=O(n) ,更新O(mlogn)、基本和堆优化的Dijkstra一样,并且写起来很麻烦→用克鲁斯阿尔算法
Kruskal算法
由于很简单,所以我们在稀疏图里面一般使用Kruskal算法。Kruskal算法是一个简单的并查集的应用。
1. 将所有边按照权重从小到大排序,可以用快排排序、sort()->O(mlogm)
2. 枚举每条边a-b(无向边),权重是c->O(m)
if a,b不连通
将这条边加入集合中
染色法
二分图当前仅当图中不含奇数环,不含奇数环一定不是二分图。
充分性:
1→黑色→分到左边;2→白色→右边
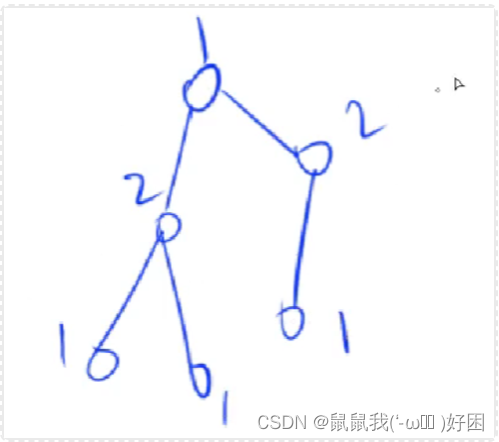
一条边的两个端点一定不属于同一个集合。只要确定了第一个点的颜色,那么所有点的颜色都确定了。由于整个图不含有奇数环,所以整个染色过程不存在矛盾!
染色完毕,我们则得到一个二分图。这样就可以把所有的点分到两个集合里面,使得所有的边处于两个集合之间的。
for(int i = 0; i <= n; i ++)
if i未染色
dfs(i, 颜色);
匈牙利算法
时间复杂度可能是线性的也不一定。
该算法可以在比较快的时间内告诉我们,左边和右边匹配成功(不存在两条边是共用一点的)的最大的数量是多少。























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








