python学习：最大公约数和最小公倍数，欧几里得算法

在 Python 中，计算最大公约数 (GCD) 和最小公倍数 (LCM) 可以通过数学公式来实现，也可以使用 Python 自带的库来简化计算。

1. 最大公约数 (GCD)

最大公约数是两个数的最大约数。可以使用 math.gcd 来直接计算，也可以通过欧几里得算法来手动实现。

使用 math.gcd 计算最大公约数：

import math

# 示例
a = 36
b = 60
gcd = math.gcd(a, b)
print(f"The GCD of {a} and {b} is: {gcd}")

欧几里得算法手动计算最大公约数：

def gcd(a, b):
    while b != 0:
        a, b = b, a % b
    return a

# 示例
a = 36
b = 60
gcd_result = gcd(a, b)
print(f"The GCD of {a} and {b} is: {gcd_result}")

2. 最小公倍数 (LCM)

最小公倍数是两个数的最小倍数。可以通过以下公式来计算：

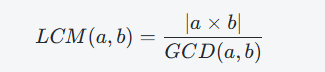
使用 math.lcm 计算最小公倍数（Python 3.9+）：

import math

# 示例
a = 36
b = 60
lcm = math.lcm(a, b)
print(f"The LCM of {a} and {b} is: {lcm}")

手动计算最小公倍数：

def lcm(a, b):
    return abs(a * b) // gcd(a, b)

# 示例
a = 36
b = 60
lcm_result = lcm(a, b)
print(f"The LCM of {a} and {b} is: {lcm_result}")

总结：

• GCD：可以通过 math.gcd 或者欧几里得算法计算。
• LCM：可以通过 math.lcm（Python 3.9及以上）或者通过公式 LCM(a, b) = abs(a * b) // GCD(a, b) 来计算。

考试使用用的是python3.8：

import math

# 求最大公约数的函数（可以直接使用math.gcd）
def gcd(a, b):
    return math.gcd(a, b)

# 求最小公倍数的函数
def lcm(a, b):
    return abs(a * b) // gcd(a, b)

# 示例
a = 36
b = 60
gcd_result = gcd(a, b)
lcm_result = lcm(a, b)

print(f"The GCD of {a} and {b} is: {gcd_result}")
print(f"The LCM of {a} and {b} is: {lcm_result}")

欧几里得算法（Euclidean Algorithm）是一种用于计算两个整数的最大公约数（GCD, Greatest Common Divisor）的经典算法。这个算法基于一个非常简单但有效的数学原理：

欧几里得算法的核心思想：

对于两个整数 a 和 b，其中 a > b，那么：

GCD(a,b)=GCD(b,a%b)GCD(a,b)=GCD(b,a%b)

也就是说，两个数 a 和 b 的最大公约数等于 b 和 a 除以 b 的余数的最大公约数。这一过程不断重复，直到余数为 0，此时的 b 就是这两个数的最大公约数。

欧几里得算法步骤：

1. 用较大的数除以较小的数，得到余数。
2. 用较小的数除以余数，得到新的余数。
3. 重复这一过程，直到余数为 0，此时最后一个非零的余数就是最大公约数。

举个例子：

计算 252 和 105 的最大公约数（GCD）。

1. 第一步：252 除以 105，余数是 42。

   252÷105=2余数42252÷105=2余数42

   所以，GCD(252,105)=GCD(105,42)GCD(252,105)=GCD(105,42)

2. 第二步：105 除以 42，余数是 21。

   105÷42=2余数21105÷42=2余数21

   所以，GCD(105,42)=GCD(42,21)GCD(105,42)=GCD(42,21)

3. 第三步：42 除以 21，余数是 0。

   42÷21=2余数042÷21=2余数0

   所以，GCD(42,21)=21GCD(42,21)=21

当余数为 0 时，算法结束，最大公约数就是最后一个非零的余数，即 21。

算法的 Python 实现：

欧几里得算法可以用递归或迭代方式实现。以下是两种实现方式：

递归实现：

def gcd_recursive(a, b):
    if b == 0:
        return a
    else:
        return gcd_recursive(b, a % b)

# 示例
a = 252
b = 105
print(f"The GCD of {a} and {b} is: {gcd_recursive(a, b)}")

迭代实现：

def gcd_iterative(a, b):
    while b != 0:
        a, b = b, a % b
    return a

# 示例
a = 252
b = 105
print(f"The GCD of {a} and {b} is: {gcd_iterative(a, b)}")

时间复杂度：

欧几里得算法的时间复杂度是 O(log(min(a, b)))，其中 a 和 b 是输入的两个整数。这意味着，算法非常高效，即使是处理大数时，也能迅速找到最大公约数。

总结：

欧几里得算法通过重复求余数来逐步缩小问题的规模，直到找到两个数的最大公约数。它是一种简单而高效的算法，被广泛应用于各种数论和计算问题中。

实例：

P1029 [NOIP 2001 普及组] 最大公约数和最小公倍数问题

初始版：

import math
x, y = map(int, input().split())
counts = 0
for a in range(x, y + 1,x):
    for b in range(x, y + 1,x): 
        if math.lcm(a, b) == y and math.gcd(a, b) == x:
            counts += 1

print(counts)

# 通过将 a 和 b 限制为 x 的倍数，减少了循环次数，从 O((y - x + 1)²)
# 降低到 O((y / x)²)，这对于 y - x 较大的情况能显著提高效率

但是时间复杂度还是高：

优化方向：

1. 筛选因子：

   • a 和 b 必须是 x 的倍数，并且 math.gcd(a, b) == x，这意味着 a 和 b 都可以写成 a = x * k 和 b = x * m 的形式，其中 k 和 m 是正整数，且 gcd(k, m) == 1。

2. 最小公倍数和最大公约数关系：

   • lcm(a, b) = lcm(x * k, x * m) = x * lcm(k, m)。
   • 因此，要求 lcm(a, b) == y，意味着 x * lcm(k, m) == y，即 lcm(k, m) == y / x。
   • 所以，我们可以减少考虑的范围，只检查满足 lcm(k, m) == y / x 的 k 和 m。

3. 改进思路：

   • 通过提前计算 y / x，然后只考虑满足 lcm(k, m) == y / x 的 k 和 m，这大大减少了不必要的循环。

个人思考：

思考
3 60

输入
x,y
输出
a,b

最小公约数 3  gcd
最大公倍数 60 lcm

lcm=x*y/gcd
x*y=lcm*gcd

对于数字a,b
排除数字a,b  1.a,b非x的倍数 2.非x*y=3*60的数字,即a*b=x*y

对于数字x,y
排除x,y 
1.y%x!=0  

2.排除x*y!=20
lcm(a,b)=lcm(x*k,y*k)=k*lcm(x,y)
lcm(15,12)=lcm(3*5,3*4)=3*lcm(5,4)
lcm(3,60)=lcm(3*1,3*20)=3*lcm(1,20)
得到x*y=20

机器人给的代码：

import math

x, y = map(int, input().split())

# 如果 y 不能被 x 整除，直接返回 0
if y % x != 0:
    print(0)
else:
    target = y // x  # 计算 lcm(k, m) 应该等于 y / x
    counts = 0
    
    # 遍历 k 和 m 的所有可能值
    for k in range(1, int(target**0.5) + 1):
        if target % k == 0:  # k 是 target 的因子
            m = target // k
            # 检查是否满足 gcd(k, m) == 1
            if math.gcd(k, m) == 1:
                counts += 2 if k != m else 1

    print(counts)

解释：

1. y % x != 0 判断：首先，如果 y 不能被 x 整除，则直接返回 0，因为 lcm(a, b) = y 不可能满足 a = x * k 和 b = x * m 的形式。

2. target = y // x：计算 lcm(k, m) 应该等于 y / x，从而减少了 a 和 b 的搜索空间。

3. k 和 m 的因子遍历：通过遍历 k 和 m 的因子，我们只需检查 lcm(k, m) == y / x 的条件。对每个 k，其对应的 m 可以通过 m = target // k 计算得到。

4. gcd(k, m) == 1：我们只考虑 gcd(k, m) == 1 的情况，这意味着 k 和 m 没有共同的因子。

5. counts += 2 if k != m else 1：对于每对满足条件的 k 和 m，如果 k 和 m 不相等，则 (k, m) 和 (m, k) 都有效，计数加 2；如果 k == m，则只计数 1。

优化效果：

通过减少搜索空间和因子对的数量，这个优化将大大降低计算复杂度。时间复杂度大约为 O(√(y / x))，比原来的 O((y - x + 1)²) 要快得多。

我自己写的：

import math
counts=0
x, y = map(int, input().split())
if y%x!=0:
    print(0)
elif y//x!=math.lcm(x,y)/x:
    print(0)
else:
    for k in range(1,int((y//x)**0.5)+1):
        if (y//x)%k==0:
            m=(y//x)//k
            if math.gcd(k,m)==1:
                counts+=2 if k!=m else 1
    print(counts)