集合|并查集|哈希

子曰:"不愤不启，不悱不发，举一隅不以三隅反，则不复也。”

孔子说:“不发奋图强时，就不启发他，不到他想说却说不出来时候，不去启发他。列举一个方面，却不能得到三个方面，就不要告诉他。”

有的时候，我们并不关心一些数据他们的关系具体怎样，我们只是关心他们是不是一伙的。

我们可以使用并查集表示一堆集合之间的关系，我们使用hash表示一个集合。

并查集是站在元素关系的角度，那些数在同一个集合。

而hash是站在集合的角度，找出这个集合有哪些元素。

https://www.luogu.com.cn/problem/P3370

我们使用字符串hash，是通过表示数的角度，也就是进制的角度。

$$\begin{array}{rl}& 定理:设b是正整数,b>1,那么每一个正整数n都可以被唯一地写成如下形式:\\ & n=a_k{b}^k+a_{k-1}{b}^{k-1}+...+a_{1}b+a_0\\ & 其中k为正整数,a_j为整数,0\le a_j\le b-1(j=0,1,...,k)且首项系数a_k\ne 0\\ & 证明:通过使用连续的带余数除法，得到这样的表示。\\ & 首先使用b除n得到\\ & n=b{q}_0+a_0,0\le a_0\le b-1\\ & 如果q_0\ne 0,那么用b除q_0得到\\ & q_0=b{q}_1+a_1,0\le a_1\le b-1\\ & q_1=b{q}_2+a_2,0\le a_2\le b-1\\ & q_2=b{q}_3+a_3,0\le a_3\le b-1\\ & ...\\ & q_{k-2}=b{q}_{k-1}+a_{k-1},0\le a_{k-1}\le b-1\\ & q_{k-1}=b\times 0+a_k,0\le a_k\le b-1\\ & 其中n=b{q}_0+a_0\\ & 我们使用第二个方程带入,n=b(b{q}_1+a_1)+a_0\\ & =b^2{q}_1+a_{1}b+a_0\\ & 再将第三个方程带入。\\ & n=b^2(b{q}_2+a_2)+a_{1}b+a_0\\ & =b^3{q}_2+a_2{b}^2+a_{1}b+a_0\\ & ...\\ & =b^{k-1}{q}_{k-2}...+a_2{b}^2+a_{1}b+a_0\\ & =b^k{q}_{k-1}+b^{k-1}{a}_{k-1}....+a_2{b}^2+a_{1}b+a_0\\ & =a_k{b}^k+a_{k-1}{b}^{k-1}...+a_2{b}^2+a_{1}b+a_0\end{array}$$
实际上我们的算法就是通过进制的思想，利用运算的技巧完善的。
$$\begin{array}{rl}& \\ & 设H_i=\sum _{j=1}^i{s}_j\times b^{i-j}\\ & 那么H_{i-1}=\sum _{j=1}^{i-1}{s}_j\times b^{i-1-j}\\ & H_i=\sum _{j=1}^{i-1}{s}_j\times b^{i-1}+b^i\\ & =b\sum _{j=1}^{i-1}{s}_j\times b^{i-1}=H_{i-1}\times b+s_i\\ & 那没[l,r]段的进制如何表示用H_i表示?\\ & H_{l,r}=\sum _{i=l}^r{s}_i\times b^{r-i}\\ & =\sum _{i=1}^r{s}_i\times b^{r-i}-\sum _{i=1}^{l-1}{s}_i\times b^{r-i}\\ & =H_r-\sum _{i=1}^{l-1}{s}_i\times b^{r-i}{b}^{l-1-r}{b}^{r+1-l}\\ & =H_r-b^{r+1-l}\sum _{i=1}^{l-1}{s}_i\times b^{l-1-i}\\ & =H_r-b^{r+1-l}{H}_{l-1}\end{array}$$

但是，我们的数字可能特别大，所以我们考虑取模的问题。

但是取了模之后，就会产生新的问题，就是虽然字符串不同，但是最后的数值确实相同的。

#include<bits/stdc++.h>
using namespace std;
#define int long long  
const int b=131;
const int mod=998244353;
const int N=1e6+10;
int t,n,m;
int h[N],H[N],pw[N];
char s[N],ans[N];
int query(int l,int r)
{
	if(l>r)return 0;
	return (H[r]-H[l-1]*pw[r-l+1]%mod+mod)%mod;
}
signed main()
{
	cin>>t;
	pw[0]=1;
	for(int i=1;i<=N;i++)
	{
		pw[i]=pw[i-1]*b%mod;
	}
	for(int i=1;i<=t;i++)
	{
		cin>>(s+1);
		n=strlen(s+1);
		int l=0;
		for(int j=1;j<=n;j++)
		{
			h[j]=(h[j-1]*b%mod+s[j]);
		}
		for(int j=min(n,m);j>=0;j--)
		{
			if(h[j]==query(m-j+1,m))
			{
				l=j;
				break;
			}
		}
		for(int j=l+1;j<=n;j++)
		{
			ans[++m]=s[j];
			H[m]=(H[m-1]*b%mod+s[j])%mod;
		}
	}
	for(int i=1;i<=m;i++)cout<<ans[i];
}

https://www.luogu.com.cn/problem/P1621

当然，有的时候集合是并查集,表示两个数之间的关系。

并查集是一种很小巧的算法。

如果经过压缩，核心部分可能只有一行。

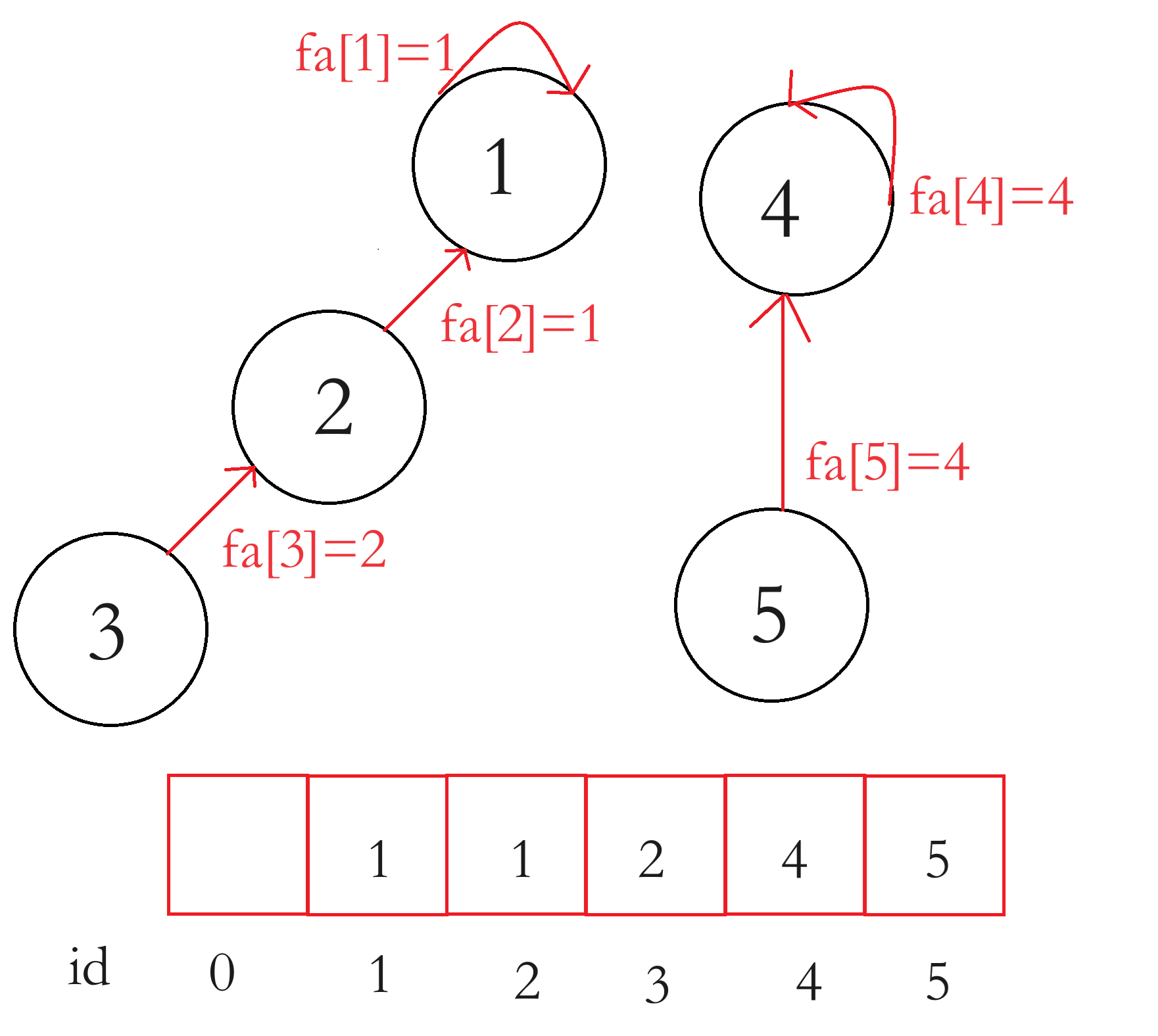
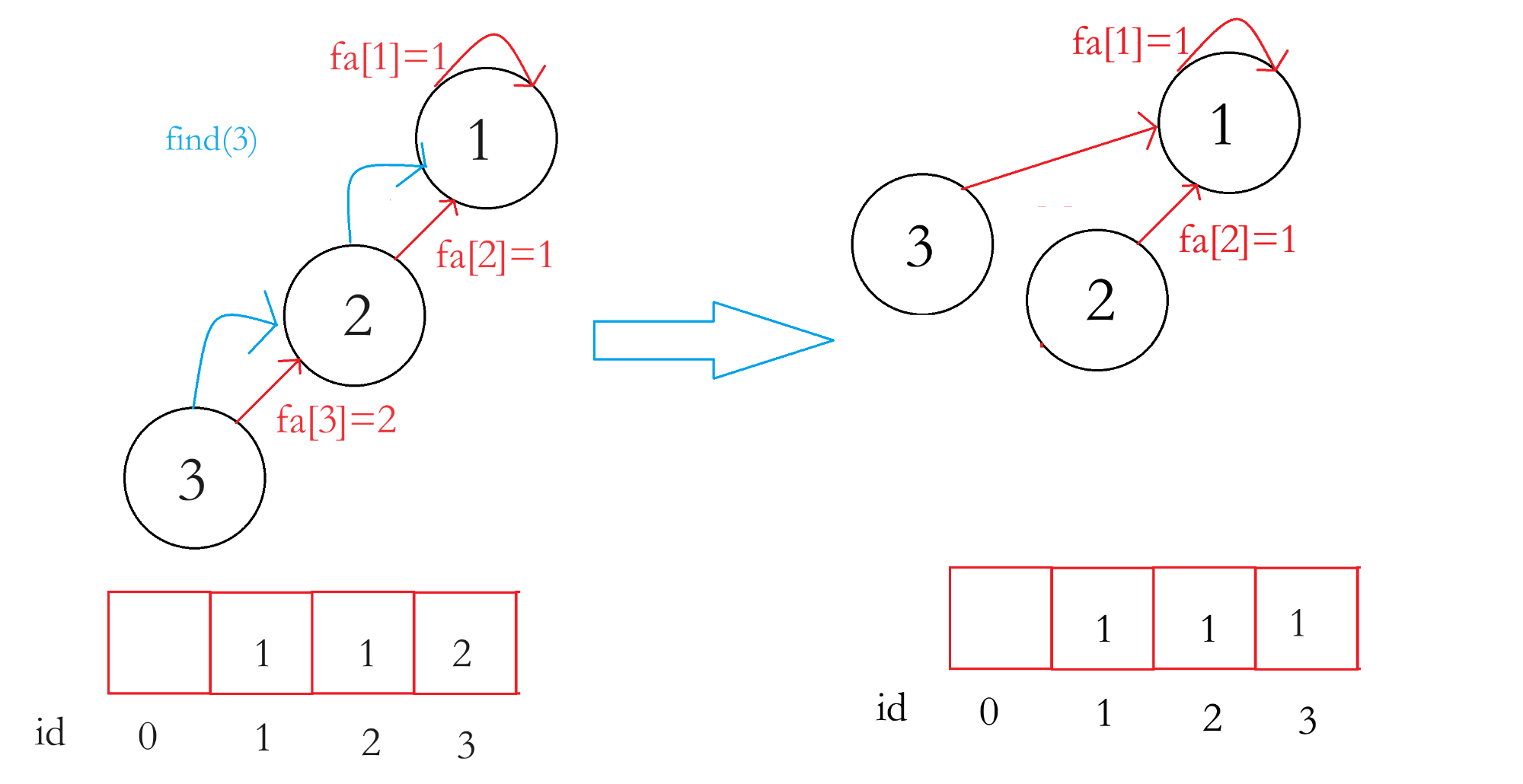
我们使用路径压缩的并查集。

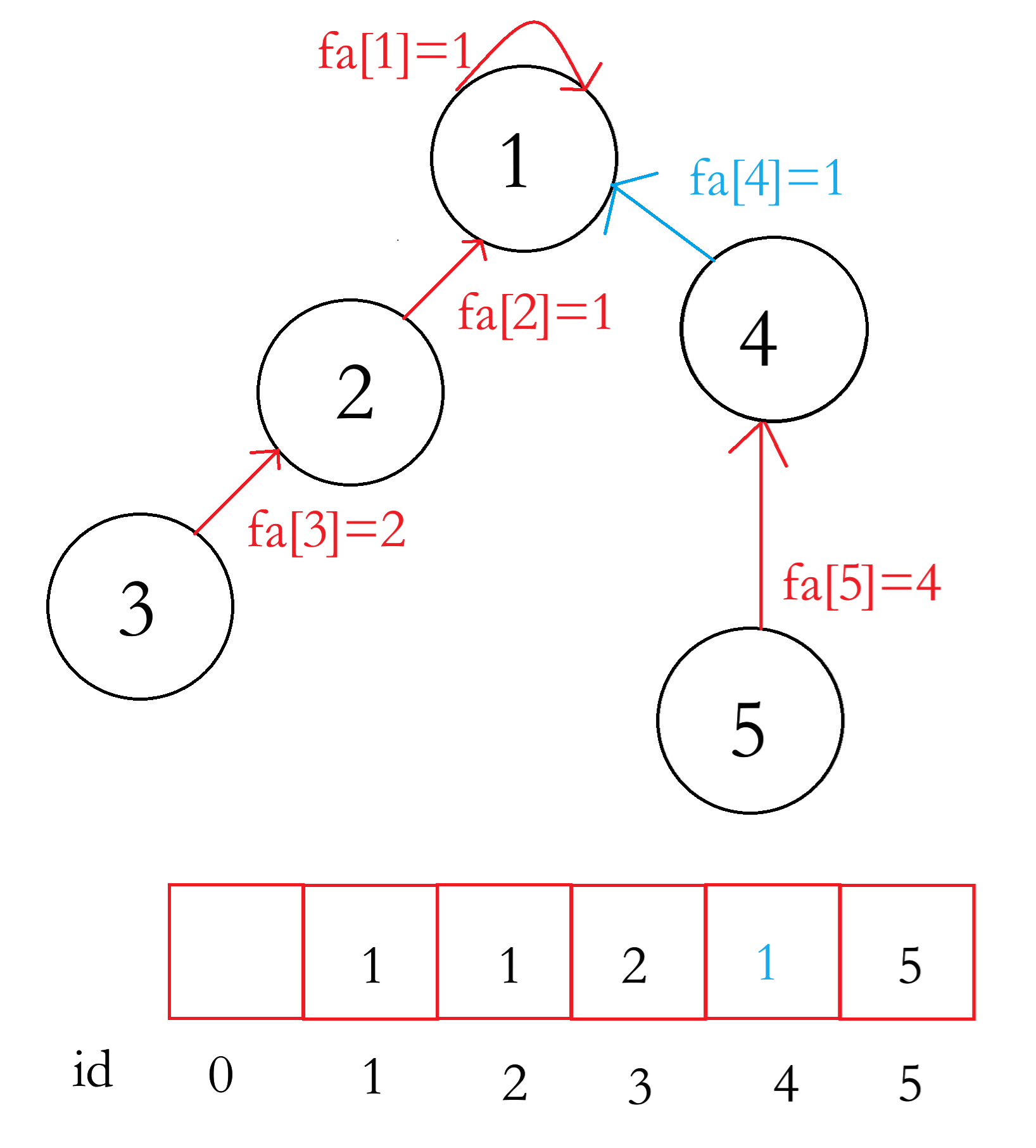
当合并的时候，我们使得其中一个指向宁外一个的根节点。

#include<bits/stdc++.h>
using namespace std;
#define int long long  
const int N=100010;
int fa[N];
int is[N];
int ans,a,b,p;
int find(int x)
{
	if(x==fa[x])return x;
	return fa[x]=find(fa[x]);
}
void unity(int a,int b)
{
	a=find(a);
	b=find(b);
	if(a!=b)
	fa[a]=b;
}
void init(int n)
{
	for(int i=1;i<=n;i++)fa[i]=i;
}
signed main()
{
	cin>>a>>b>>p;
	init(b);
	for(int i=2;i<=b;i++)
	{
		if(!is[i])
		{
			int pre=0;
			for(int j=i;j<=b;j+=i)
			{
				is[j]=true;
				if(i>=p&&j>=a)
				{
					if(pre==0)
					pre=j;
					else 
					unity(pre,j);
				}
			}
		}
	}
	for(int i=a;i<=b;i++)
	{
		if(fa[i]==i)
		ans++;
	}
	cout<<ans;
}

https://www.luogu.com.cn/problem/P1525

此题蕴含了否定只否定的思想。

我们将这个问题用数学语言表达，在一张图中，
我们希望二染色,使得两个同色节点之间的边权值最小。

我们可以使用一种贪心的思维，首先使得权值最大的边不成立，然后使得权值第二大的边不成立。

这条边能不能成立取决于能不能染不同的颜色。

这就可以使用并查集了。

如果在同一个块中，他们就具有关系了，需要判断他们的关系

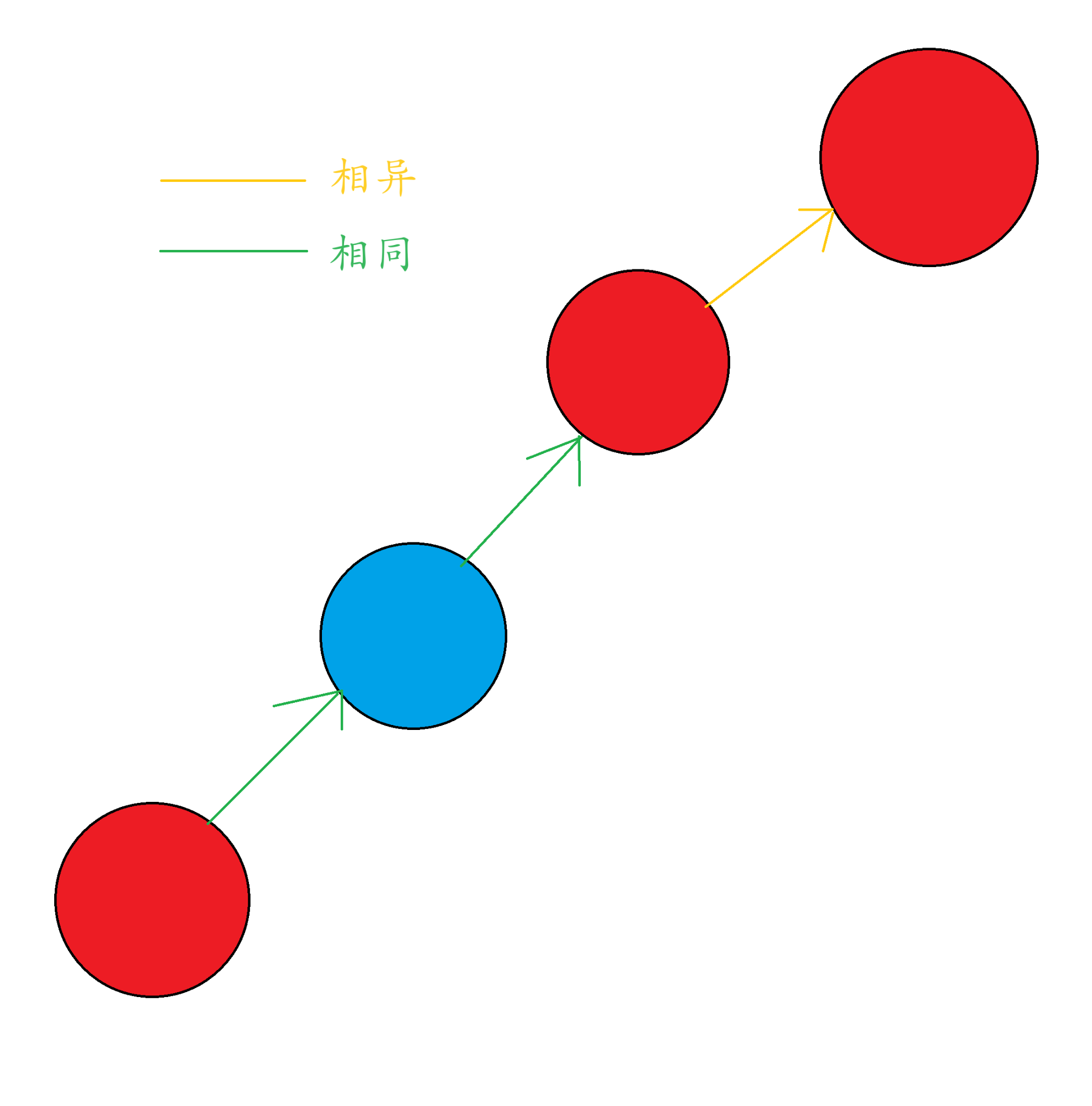
如果在不同块中，那么可以合并。
但是合并的时候需要判断添加的边是无权边还是加权边。

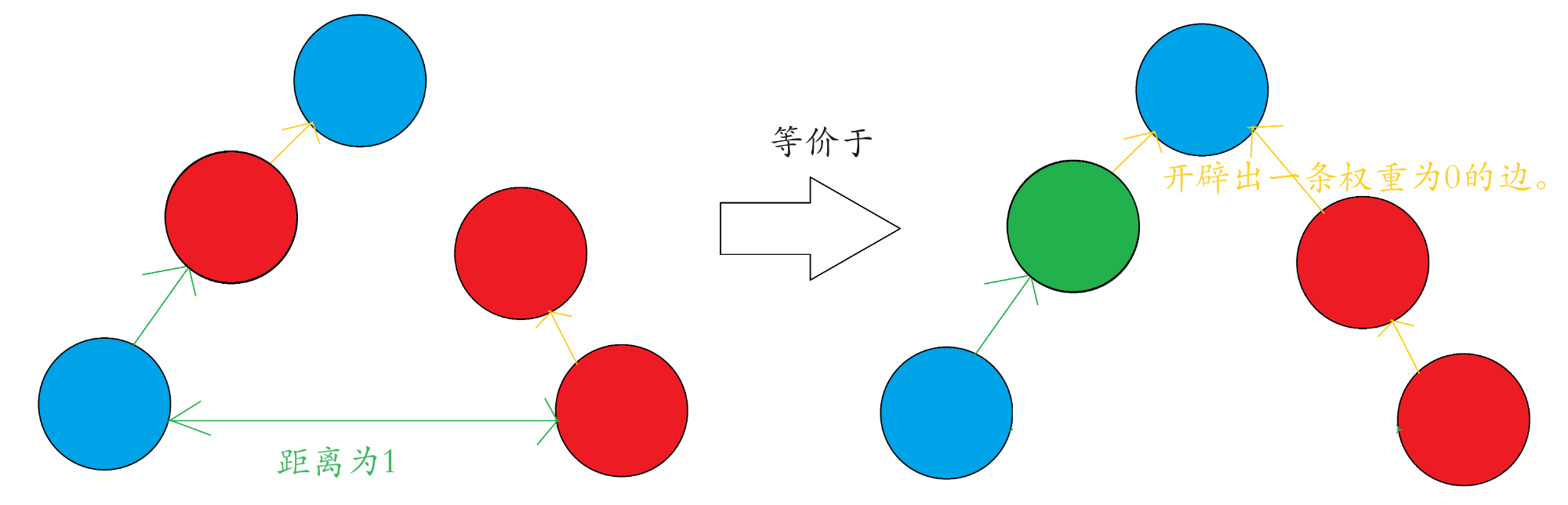
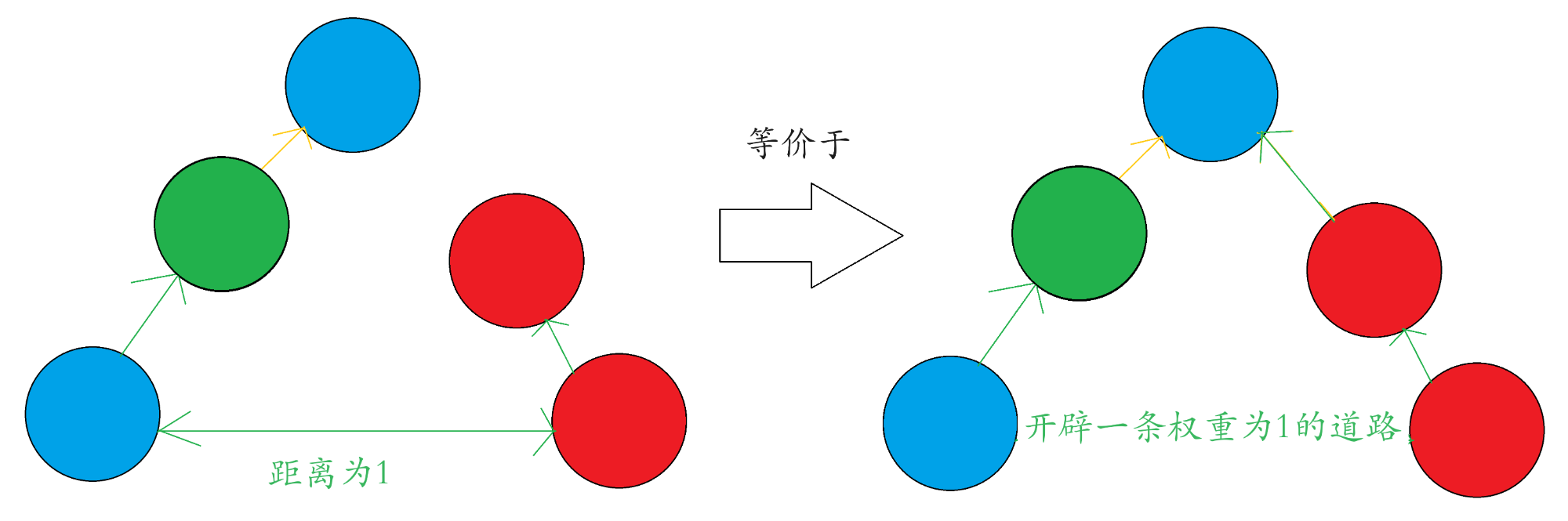
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=100010,M=3*N;
int p[N],d[N];
int n,m;
struct  Edge
{
   int a,b,w;
   bool operator<(const Edge&b)const 
   {
   	return w>b.w;
   }
}edge[M];
int find(int x)
{
   if(p[x]!=x)
   {
   	int u=find(p[x]);
   	d[x]+=d[p[x]];
   	p[x]=u;
   }
   return p[x];
}
int res=0;
signed main()
{
   cin>>n>>m;
   for(int i=1;i<=n;i++)
   {
   	p[i]=i;
   	d[i]=0;
   }
   for(int i=0;i<m;i++)
   {
   	int a,b,c;
   	cin>>a>>b>>c;
   	edge[i]={a,b,c};
   }
   sort(edge,edge+m);
   for(int i=0;i<m;i++)
   {
   	int a=edge[i].a;
   	int b=edge[i].b;
   	int w=edge[i].w;
   	int pa=find(edge[i].a);
   	int pb=find(edge[i].b);
   	if(pa==pb)
   	{
   		if((d[a]+d[b])%2==0)
   		{
   			cout<<w;
   			return 0;
   		}
   	}
   	else 
   	{
   		if((d[a]+d[b])&1)
   		{
   			p[pa]=pb;
   			d[pa]=0;
   		}
   		else {
   			p[pa]=pb;
   			d[pa]=1;
   		}
   	}
   }
   cout<<res;
}