课上实验反思，matlab，2FSK调制解调时带通滤波器与低通滤波器的设计。

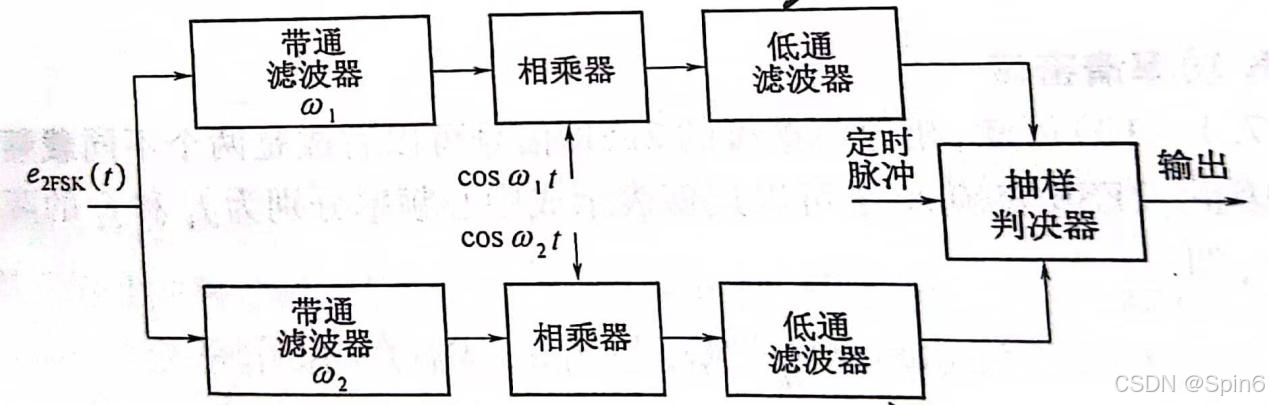
（2FSK相干解调原理图）

（2FSK非相干解调原理图）

①2FSK相干（非相干）解调时带通滤波器的作用：

带通滤波器将

分成载波为w1与w2的两路信号，同时滤除带外噪声。

②带通滤波器如何设计：

带通滤波器的设计要根据输入信号的带宽、中心频率去设计滤波器的通带截止频率、阻带截止频率、中心频率。

输入信号是2FSK已调信号，其带宽为

（

码元速率），其载波频率分别是Fc1=Rb*4; Fc2=Rb*8，2FSK已调信号可以看成是两个2ASK相加，2ASK信号的传输带宽是码元速率的2倍，因此滤波器的通带带宽是2Rb，中心频率分别是Fc1、Fc2。

%%用窗函数设计带通滤波器（blackman窗） Matlab用fir1（M,wc,window）分别是M滤波器阶数（等于长度N-1）、wc归一化截止频率（

）、window窗函数的类型。

function [x_bp] =FSK_bandpass(x,Fc,fs,Rb) wsl=2*pi*(Fc-2*Rb)/fs;    %阻带上截止角频率 wsh=2*pi*(Fc+2*Rb)/fs;    %阻带下截止角频率 wpl=2*pi*(Fc-1*Rb)/fs;  %通带上截止角频率 wph=2*pi*(Fc+1*Rb)/fs;  %通带带下截止角频率  wph减去wpl等于2Rb B=min((wpl-wsl),(wsh-wph));  %最小过渡带宽度 N=ceil(11*pi/B);             %滤波器阶数（根据布莱克曼窗计算的滤波器阶数） %%计算滤波器系数 wl=(wsl+wpl)/2/pi;  %上截止频率 6dB截止频率 wh=(wsh+wph)/2/pi;  %下截止频率 6dB截止频率 wc=[wl,wh];         %设置理想带通截止频率 b=fir1(N-1,wc,blackman(N));         %设置滤波器系数 b_l2 = fix(length(b)/2); len= length(x); x_bandpass1 = conv(x,b); x_bp(1:len) = x_bandpass1(b_l2 : b_l2 + len -1);%去除滤波器延时 end

③2FSK相干解调时低通滤波器的作用：

带通滤波器输出的信号是

，经过相乘器后输出的信号是

，因此低通滤波器将2w1的高频分量滤除。

④低通滤波器如何设计：

经过低通滤波器后要得到的是基带信号s(t)，所以要根据基带信号的带宽去设置低通滤波器的通带截止频率、阻带截止频率。

此实验基带信号s(t)是单极性非归零码，因此基带信号的带宽是

也就是码元速率Rb。因此低通滤波器的通带宽度是Rb.

%用窗函数设计带低滤波器（hanning窗）Matlab用fir1（M,wc,window）分别是M滤波器阶数（等于长度N-1）、wc归一化截止频率（

）、window窗函数的类型。

function [ x_lowpass ] = FSK_lowpass( x,fs,Rb )     ws=Rb;                    %通带截止频率     ws1=2*Rb;                  %阻带起始频率     wt=2*pi*ws/fs;                  %经采样后的通带截止角频率     wz=2*pi*ws1/fs;                 %阻带的起始频率     wc=(wt+wz)/2;                   %滤波器6dB截止频率 未归一化     N=ceil(6.6*pi/(wz-wt));              b=fir1(N-1,wc/pi,hanning(N));   %滤波器时域函数,滤波系数 ，采用hanning窗实现低通滤波       b_l2 = fix(length(b)/2);     len= length(x);     x_lowpass1 = conv(x,b);%卷积     x_lowpass(1:len) = x_lowpass1(b_l2 : b_l2 + len -1); end

⑤Hilbert变换

Hilbert变换的本质是原信号与

卷积，物理意义是将原信号相位延迟90°经过变换后的信号作为虚部，原信号作为实部构成解析信号，求解析信号的模从而得到原信号的包络。