机器学习 特征工程

 目录

一、特征提取

1、DictVectorizer 字典列表特征提取

2、CountVectorizer 文本特征提取

3、TfidfVectorizer 文本特征词的重要程度特征提取

二、无量纲化

1、MinMaxScaler归一化

2、normalize归一化

3、StandardScaler 标准化

三、特征降维

1、特征选择

a、低方差过滤特征选择 VarianceThreshold

b、相关系数特征选择

2、主成分分析 PCA

---

在机器学习时，我们获得的原始数据往往会存在以下问题：信息冗余或无关（如无关字段、重复特征）；格式不适合模型（如文本、类别数据需要数值化）；缺失值或噪声（如数据采集错误）；维度灾难（特征过多导致计算效率低）等，所以在对数据集进行进一步操作之前就需要特征工程，即将任意数据(如文本或图像)转换为可用于机器学习的数字特征，比如字典特征提取(特征离散化)、文本特征提取、图像特征提取等，它分为以下几个步骤：特征提取、无量纲化、降维，下面来依次介绍：

一、特征提取

特征提取是特征工程的核心步骤，它的API应用主要有两步：首先先实例化一个转换器对象，再调用fit_transform()方法进行转换。对不同类型的数据进行特征提取时用到的转换器也不同，下面介绍常用的四种：

1、DictVectorizer 字典列表特征提取

当原始数据是字典（Dict）或字典列表形式时，需要将其转换为数值矩阵供模型使用，这时DictVectorizer转换器就派上了用场，代码示例如下：

from sklearn.feature_extraction import DictVectorizer
data = [{'city':'成都', 'age':30, 'temperature':20}, 
        {'city':'重庆','age':33, 'temperature':60}, 
        {'city':'北京', 'age':42, 'temperature':80},
        {'city':'上海', 'age':22, 'temperature':70},
        {'city':'成都', 'age':72, 'temperature':40},
       ]
dictvec = DictVectorizer(sparse=False) #实例化一个dictvec对象并返回稠密矩阵
datanew = dictvec.fit_transform(data) #对象调用方法转换原始数据
print(datanew, type(datanew))
print(dictvec.get_feature_names_out()) #获取特征值的字段名并打印

运行结果如下：

说明返回的这个数组矩阵的第一列表示“age”，因为它的特征值都是数字所以直接保留了原值，第二例表示“city=上海”，如果为0则表示不等于上海，后面的以此类推。

如果想看得更直观可以引入pandas然后：

# print(datanew, type(datanew))
# print(dictvec.get_feature_names_out()) #获取特征值的字段名并打印
print(pandas.DataFrame(datanew, columns=dictvec.get_feature_names_out()))

其他保持不变，运行结果：

这里要解释两点：第一，sparse=True代表返回的是稀疏矩阵，即一个矩阵中大部分元素为零，只有少数元素是非零的矩阵，而sparse=False则代表返回的是稠密矩阵，是指矩阵中非零元素的数量与总元素数量相比接近或相等，也就是说矩阵中的大部分元素都是非零的。在实际应用中，选择使用稀疏矩阵还是稠密矩阵取决于具体的问题场景和数据特性；第二，fit_transform()方法其实是fit()+transform()一步到位完成学习和转换，单独的fit()方法是用于计算数据（均值和标准差等），transform()是使用fit()计算的结果对数据进行转换，要分开使用的原因是对训练集可以一步到位用fit_transform()方法，但是对测试集不需要fit()，直接应用训练集的计算结果进行transform()即可。

2、CountVectorizer 文本特征提取

它适用于将文本数据转换为（每个词出现的次数）矩阵，英文文本默认按空格分割，中文文本需配合分词工具比如jieba，示例如下：

提取英文文本：

'''英文文本提取'''
    from sklearn.feature_extraction.text import CountVectorizer
    data=["life is well, life is great", "we like life"]

    countvec = CountVectorizer(stop_words = ["is"]) #不提取“is”
    datanew = countvec.fit_transform(data) #进行转换
    print(countvec.get_feature_names_out())
    print(datanew)
    # print(datanew.toarray())

运行结果为三元组表：

这是一种存储形式，稀疏矩阵通常用这种三元组表的形式来存储非零元素，表示第0行第一列的值是2，第0行第四列的值是1，依此类推。而CountVectorizer转换器会默认返回稀疏矩阵，所以我们通常用toarray()方法将其转换为数组表示，即：

 # print(datanew)
 print(datanew.toarray())

其他不变。运行结果：

同样的如果想看得更直观：

print(pd.DataFrame(datanew.toarray(), index=["句子1","句子2"] ,columns=countvec.get_feature_names_out()))

运行结果：

提取中文文本：

首先用pip install命令下载jieba分词工具，它的具体用法如下：

 import jieba
    str1 = "我爱学习学习爱我"
    str2 = jieba.cut(str1) #jieba内置方法
    res = list(str2) #转换成列表输出
    print(res)

运行结果：

可以返回用空格连接的字符串：

# print(res)
str3 = " ".join(list(res))
print(str3)

其他不变，运行结果：

完整代码示例如下：

from sklearn.feature_extraction.text import CountVectorizer
import jieba
def word_cut(text): #封装函数
    str1 = jieba.cut(text)
    res = list(str1)
    return " ".join(res)

words = ["现在正在提取中文文本","相信我们一定可以的"]
countvec = CountVectorizer(stop_words=["的"])
arr = [word_cut(item) for item in words] #遍历每一句文档并调用函数进行分词，并将结果包装成列表
wordsnew = countvec.fit_transform(arr)
# print(arr) #['现在 正在 提取 中文 文本', '相信 我们 一定 可以 的']

print(countvec.get_feature_names_out())
print(wordsnew.toarray())

这段代码首先封装了一个函数，功能是把中文字符串中进行分词(会忽略长度小于等于1的词语，因为它们往往缺乏语义信息，不能很好地表达文本的特征)，然后返回一个用空格连接的字符串。

接着实例化了一个countvec对象并对”的“字不进行提取，然后就调用封装的函数对文本进行分词，如果有多个文本可以用列表推导式遍历，注意这里一定要将结果包装成列表，因为接下来的CountVectorizer.fit_transform()需要传入的是一个可迭代的文本，传入之前可以先打印一下看是否处理成功，然后就可以进行转换。

运行结果：

3、TfidfVectorizer 文本特征词的重要程度特征提取

首先要知道 TF-IDF算法：

TF-IDF是一种用于评估单词在文档中重要程度的统计方法，它结合了两个指标：TF词频和IDF逆文档频率。TF表示一个词在当前文档中的重要性，IDF反映了该词在整个文档中的稀有程度，所以TF-IDF值越高，说明这个词对当前文档越重要。

计算方法如下：

                        

例如文档1 = ”I love eating, love Python, love coding.“，则 love的TF=3/6=0.5，Python的TF=1/6≈0.17，表示 love的出现次数比 Python多（默认情况下不考虑 ”I“、”a“、”is“、”the“等常见但对语义贡献很小的词）

                       

例如总文档数 N=100，单词 love在19个文档出现过，Python在4个文档出现过，则 love的IDF=log(100/20)≈1.609，Python的IDF=log(100/5)≈2.996，表示 love的罕见度比 Python低

                    

所以单词 love的TF-IDF= 0.5x1.609=0.804，Python的TF-IDF=0.17x2.996=0.509，表示 love的综合权重比 Python更高，对整个文档的贡献更大。通过这种算法可以过滤掉高频但无意义的词（如“的”、“I”），突出文档特有的关键词。

那么 TfidfVectorizer转换器就会自动完成这个算法，与CountVectorizer的示例基本相同，仅仅把CountVectorizer改为TfidfVectorizer即可 ：

def cut(text): #封装函数
    str1 = jieba.cut(text)
    res = list(str1)
    return " ".join(res)

words = ["教育学会会长任职期间，坚定支持民办教育事业！",  "扶持民办,学校发展事业","事业做出重大贡献！"]
tfidf = TfidfVectorizer(stop_words=["事业","期间","教育"])
arr = [cut(item) for item in words]
wordsnew = tfidf.fit_transform(arr)

print(tfidf.get_feature_names_out())
print(wordsnew.toarray())

运行结果如下：

 用dataframe结构查看：

print(pd.DataFrame(wordsnew.toarray(),columns=tfidf.get_feature_names_out()))

 运行结果（用jupyter好看一点）：

 每个数字代表每个词在当前文档里的TF-IDF

二、无量纲化

 无量纲化（也称为标准化或归一化）是指通过数学变换，消除数据中不同特征之间的量纲（单位）和数量级差异，使得所有数据变为无单位的纯数值（比如0到1之间），在同一尺度上可比。下面介绍三种无量纲化方式：

1、MinMaxScaler归一化

最小-最大归一化是将原始数据线性变换到某一范围（默认为0-1）：

                                         

这里的 xmin 和 xmax 分别是每种特征中的最小值和最大值，而 x是当前特征值，Xscaled 是归一化后的特征值。

API为 MinMaxScaler(feature_range)，参数feature_range表示归一化后的值域，可以自己设定，然后再用 fit_transform()函数对原始数据进行归一化，原始数据类型可以是list、DataFrame和ndarray，下面用list示例：

def test3():
    '''最大最小值归一化'''
    from sklearn.preprocessing import MinMaxScaler
    data=[[1.75,15000,120],
         [1.5,16000,140],
         [1.6,20000,100]]
    minmax = MinMaxScaler(feature_range=(0,1)) #实例化对象并设置值域
    datanew = minmax.fit_transform(data) #对原数据进行转换
    print(datanew)

运行结果：

该方法严格限定范围，适合数据分布较均匀的情况，缺点是最大值和最小值容易受到异常点影响，所以容错性比较小

2、normalize归一化

有三种方式，一种是L1归一化，用曼哈顿距离计算，即将所有特征值的绝对值相加作为分母,当前特征值作为分子；另一种是L2归一化，用欧氏距离计算，即将所有特征值的平方相加作为分母，当前特征值作为分子；还有一种是max归一化，将特征值中的max作为分母，当前特征值作为分子。API为 normalize(data, norm= , axis=1)，norm可选参数有l1, l2, max：

代码示例如下，这里用 l2：

def test4():
    '''normalize归一化'''
    from sklearn.preprocessing import normalize
    data=[[1.75,15000,120],
         [1.5,16000,140],
         [1.6,20000,100]]
    normal = normalize(data, norm="l2", axis=1)
    print(normal)

运行结果：

剩下的 l1、max可自行尝试

3、StandardScaler 标准化

 标准化也称为数据归一化或特征缩放。它的目的是将不同特征的数值范围缩放到统一的标准范围，以便更好地适应一些机器学习算法。

最常见的标准化方法是Z-score标准化，也称为零均值标准化，它通过对每个特征值减去其均值，再除以其标准差，将原始数据转换为均值为0，标准差为1的分布。公式如下：

                                               

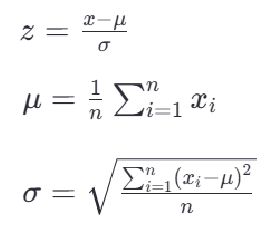
其中，z是原始数据经过转换后的值，x是原始数据，μ是该特征的均值，σ是该特征的标准差

举个例子，假设某数据集包含“年龄”和“收入”：

                                                

此时年龄的均值是35，标准差经过计算约等于15，则 z(20) =（20-35）/15≈ -1，收入的均值是45，标准差≈35，则z(80) = （80-45）/35 = 1

代码如下，用法基本与MinMaxScaler相同，就是实例化对象时不需要填参数：

def test5():
    '''StandardScaler标准化'''
    from sklearn.preprocessing import StandardScaler
    data=[[1.75,15000,120],
         [1.5,16000,140],
         [1.6,20000,100]]
    
    sts = StandardScaler() #实例化对象
    datanew = sts.fit_transform(data) #转换数据
    print(datanew) 

运行结果：

注意，当预处理数据时，首先需要在训练集上使用 fit_transform()，这样做可以一次性完成统计信息的计算和数据的标准化，然后再对测试集使用transform方法，因为不希望测试集的信息影响到训练过程。总结来说，常常是先 fit_transform训练集，然后再 tansform测试集。

三、特征降维

在实际数据中，有时候特征很多，会增加计算量，降维主要用于减少数据集中的特征数量，同时尽可能保留原始数据的关键信息，下面介绍两种特征降维方式：

1、特征选择

a、低方差过滤特征选择 VarianceThreshold

其实是 Filter过滤法，即按统计指标（如方差、卡方检验、互信息等）选择特征，这里选择方差所以叫”低方差过滤“，方差就表示每个值与平均值的离散程度，步骤就是计算每个特征在训练集中的方差，然后选择一个方差阈值，低于这个阈值的方差代表的特征会被移除，代码如下：

def test6():
    from sklearn.feature_selection import VarianceThreshold 
    data = [[11,2],
            [10,7],
            [10,12],
            [10,22],
            [10,5],
            [11,9],
            [10,3],
            [10,2]]
    var = VarianceThreshold(threshold=2.0) #实例化对象，令方差阈值为2
    datanew = var.fit_transform(data) #一步到位转换原始数据
    print(datanew)

注意 threshold参数为浮点型

运行结果：

可以看到，第一列的特征已经被过滤掉了

b、相关系数特征选择

首先了解两个性质：正相关性和负相关性。

正相关性是指两个变量之间的一种统计关系，其中一个变量的增加通常伴随着另一个变量的增加，反之亦然。在正相关的关系中，两个变量的变化趋势是同向的，当我们说两个变量正相关时，意味着如果第一个变量增加，第二个变量也有很大的概率会增加，但并不意味着一个变量的变化直接引起了另一个变量的变化，它仅仅指出了两个变量之间存在的一种统计上的关联性。这种关联性可以是因果关系，也可以是由第三个未观察到的变量引起的，或者是纯属巧合。

负相关性与正相关性刚好相反，但是也说明相关，比如运动频率和BMI体重指数程负相关，同样不意味着一个变量的变化直接引起了另一个变量的变化

那么常用的相关系数模型就是皮尔逊相关系数，它是一种度量两个变量之间线性相关性的统计量。它提供了两个变量间关系的方向（正相关或负相关）和强度的信息，其取值范围是 [−1,1]，

• r=1：完全正线性相关

• r=-1：完全负线性相关

• r≈0：无线性关系

若越接近1则表示越强正相关，越接近-1则越强负相关。

API为 pearsonr()，要求必须传入两个相同的长度一维数组，如果数据是二维数组或多维，可以用 flatten()方法展平成一维，代码如下：

def test7():
    from scipy.stats import pearsonr
    x=np.array([[11,2],
      [10,7],
      [10,12],
      [10,22],
      [10,5],
      [11,9],
      [10,3],
      [10,2]],dtype=np.float32)
    y=np.array([[2],
      [70],
      [120],
      [220],
      [50],
      [90],
      [30],
      [20]],dtype=np.float32)
    
    # pea1 = pearsonr(x[:,0].flatten(), y.flatten()) #将x中下标为0的列展平，即第一列展平
    pea2 = pearsonr(x[:,1].flatten(), y.flatten()) #将x中下标为1的列展平，即第二列展平

    # print(pea1.statistic) #打印皮尔逊系数 -0.2578938702789001
    print(pea2.statistic) #0.9963498055876245

statistic 通常指的是计算得到的相关系数 r 本身

2、主成分分析 PCA

核心思想是：把复杂的数据变简单，同时尽量保留有用的信息。

举个例子直观理解，比如现在有一张成绩单，包含语文成绩、数学成绩、英语成绩，这些科目可能高度相关（数学好的同学，英语可能也不错）导致数据冗余，所以这时想要描述这个学生的综合能力就可以用PCA，首先找到“主成分”，比如“理科能力”和“文科能力”，用这两个维度代替原来的3科成绩，然后降维，从3D（数学、语文、英语）→ 2D（理科能力、文科能力）。或者用“身高”和“体重”代替“头围、臂长、腿长…”来描述一个人的体型，也是利用了PCA

API为 PCA(n_components= )，参数填小数表示降维后保留百分之多少的信息，填整数表示降到几维，但不能保证保留的信息有多少。代码示例如下：

参数为小数：

def test8():
    '''PCA主成分分析'''
    from sklearn.decomposition import PCA
    data = [[2,8,4,5], 
            [6,3,0,8], 
            [5,4,9,1]]
    
    pca = PCA(n_components=0.8) #保留原始数据80%的信息
    datanew = pca.fit_transform(data)
    print(datanew)

运行结果：

参数为整数：

 # pca = PCA(n_components=0.8)
   pca = PCA(n_components=3) #降到3维

运行结果：

可以看到，原来的数据是4维，成功降到了3维

主成分分析的原理这里没有介绍，可以自行了解。

特征工程到这里就结束，下一篇机器学习是KNN算法、模型选择与调优，以上有问题可以指出。