xtu oj 六边形

题目描述

一个六边形组成的“花朵”图案，编号如图所示。

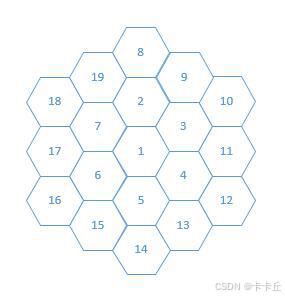
其中2∼7 构成内圈，8∼19构成外圈。 你可以按顺时钟或者逆时针方向，循环移动外圈或者内圈六边形里数字，但是不能在内外圈之间移动里面的数字。

任取一个六边形和其周围围绕的六个六边形，可以构成的一个“小花”图形，我们想知道所有这样的“小花”中的数字累加和最小是多少？

输入格式

第一行输入一个整数𝑇 (1≤𝑇≤1000)，表示样例的个数。

以后每个样例占1行，为19个非负整数，每个数的值不超过1000，为对应编号格子中的数字。

输出格式

每行输出一个样例的结果，为一个整数。

样例输入

1
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19

样例输出

28

样例解释

无论怎么旋转内外圈，中央的那个子六边形的累计和都是1+2+3+4+5+6+7=28，这个是最小的。

思路

注意是按照图中序号的位置依次填写值，并且只考虑这个图形中所有六边形，由图形画出所有六边形一定包含序号1，将构成的6边形分成2种情况，第一种包括中央的子六边形，六边形分为内外2圈，另一种情况一定包括内圈的连续3个外圈连续3个和中央6边形，分别计算内圈的连续3个外圈连续3个六边形的最小值；比较2种情况的最小值

代码：

#include<stdio.h>
int main()
{
	int t;
	scanf("%d",&t);
	while(t--){
		int a[20] = {0};//sum计算前序和
		for(int i=1;i<20;i++){
			scanf("%d",&a[i]);
		}
		int min =  a[1]+a[2]+a[3]+a[4]+a[5]+a[6]+a[7];//最内侧
		int min1 = 7000,min2 = 7000;
		for(int i=2;i+2<8;i++){
		   if(min1>a[i]+a[i+1]+a[i+2])
			   min1 = a[i]+a[i+1]+a[i+2];
		}
		if(a[2]+a[3]+a[7]<min1)
			min1 = a[2]+a[3]+a[7];
		if(a[2]+a[6]+a[7]<min1)
			min1 = a[2]+a[6]+a[7];
		for(int i=8;i+2<20;i++){
			if(min2>a[i]+a[i+1]+a[i+2])
				min2 = a[i]+a[i+1]+a[i+2];
		}
		if(a[18]+a[19]+a[8]<min2)
			min2 = a[18]+a[19]+a[8];
		if(a[19]+a[8]+a[9]<min2)
			min2 = a[9]+a[19]+a[8];
		if(min>min1+min2+a[1])
			printf("%d\n",min1+min2+a[1]);
		else
		printf("%d\n",min);
	}
}