求四阶行列式的值

include <stdio.h>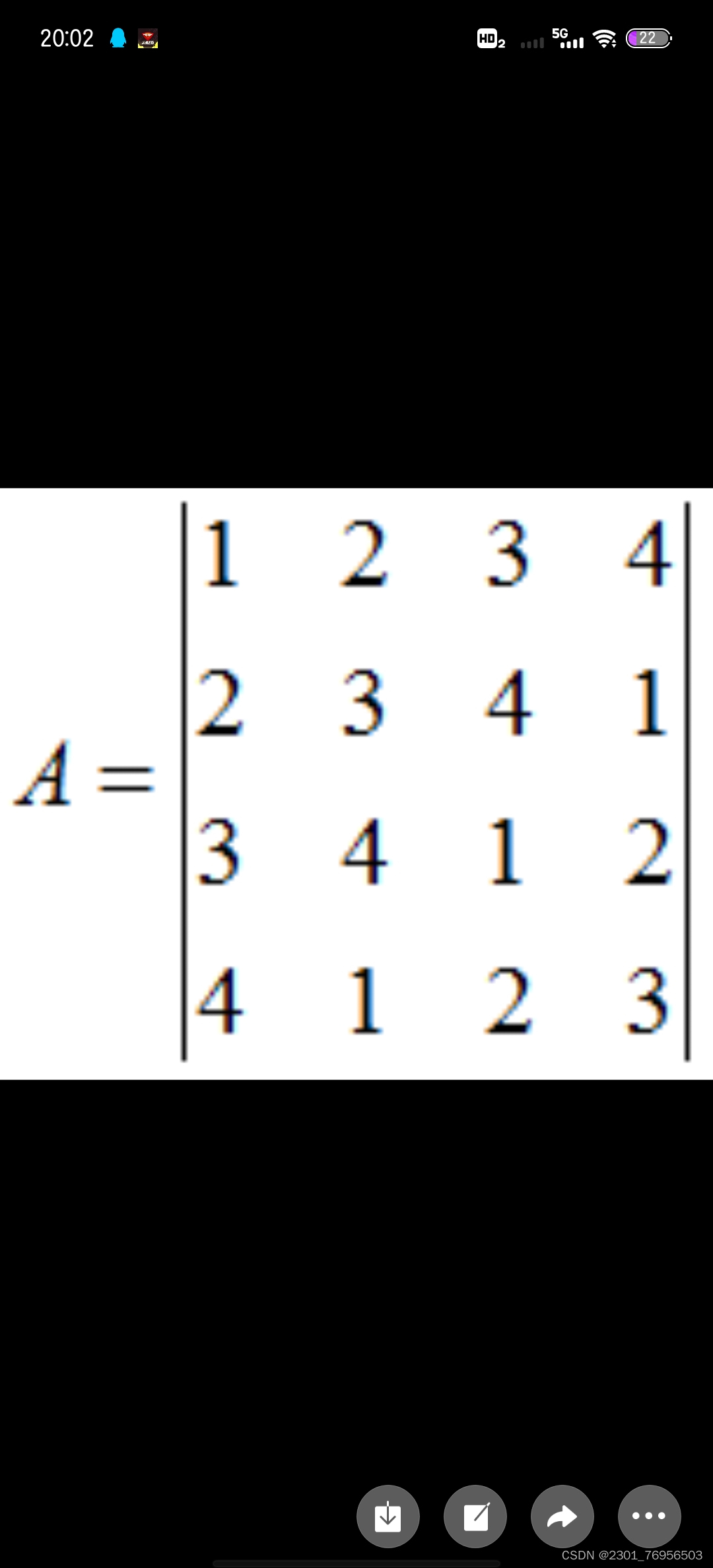
int main()
{
    int a[4][4] = { {1,2,3,4},{2,3,4,1},{3,4,1,2},{4,1,2,3 }//定义一个而为数组，并将其初始化
};
    int i, j;double m,A;
    //将矩阵化为上三角型后，计算对角元素相乘值，即为行列式的值
    for (i = 1; i < 4; i++) 
    {
        m = a[i][0] / a[0][0];
        for (j = 0; j < 4; j++) { a[i][j] = a[i][j] - a[0][j]*m; }
    }
    for (i = 2; i < 4; i++) 
    { m = a[i][1] / a[1][1];
    for (j = 1; j < 4; j++) { a[i][j] = a[i][j] - a[1][j] * m; }
    }
    for (i = 3; i < 4; i++)
    {
        m = a[i][2] / a[2][2];
        for (j = 2; j < 4; j++) { a[i][j] = a[i][j] - a[2][j] * m; }
    }
    A = a[0][0] * a[1][1] * a[2][2] * a[3][3]; printf("对角线元素为%d,%d,%d,%d\n", a[0][0], a[1][1], a[2][2], a[3][3]);
    printf("行列式的值为%f\n", A);
    system("pause");
    return 0;
}