首先打开工具的使用然后用具体的实例来进行演示,(这里我给出10进制的演示方法)
如果给出的全部是数字就选用16进制,如果给出的是含有数字和字母的就选用16进制。
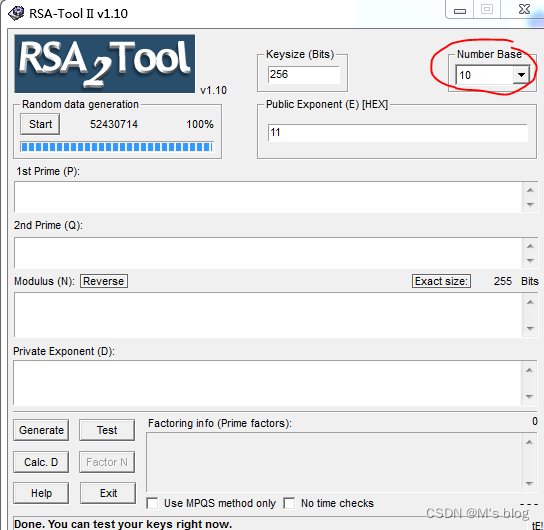
给出p=3,q=5,点击Calc.D即可自动算出N和D的值,如果已知N的值,点击Generate即可拿到P和Q的值,再点击test即可进行加密解密操作。

M是输入的明文,C是加密后的结果,在输入名文的时候只能EN键能够点击,DE键不能够点击。(一般RSA都是用python脚本跑的,比如CTF当中的密码题)。
首先打开工具的使用然后用具体的实例来进行演示,(这里我给出10进制的演示方法)
如果给出的全部是数字就选用16进制,如果给出的是含有数字和字母的就选用16进制。

给出p=3,q=5,点击Calc.D即可自动算出N和D的值,如果已知N的值,点击Generate即可拿到P和Q的值,再点击test即可进行加密解密操作。

M是输入的明文,C是加密后的结果,在输入名文的时候只能EN键能够点击,DE键不能够点击。(一般RSA都是用python脚本跑的,比如CTF当中的密码题)。

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


