Prim算法(858. Prim算法求最小生成树，朴素版Prim)(带图讲解，超详细)(带上了保存路径)

前言

   本专栏博客将会带大家讲解图论中的最小生成树问题和二分图问题。

   其中最小生成树中有两种算法，一种是Prim算法，Prim算法又分为朴素版的Prim（时间复杂度$O(n^2)$）和堆优化版的Prim（时间复杂度$O(mlogn)$）（跟Dijkstra算法分类一样，写法也很类似）；另一种是Kruskal算法（时间复杂度$O(mlogm)$）。

   朴素版Prim算法适合用稠密图，而堆优化版Prim和Kruskal算法适合用稀疏图。堆优化版的Prim算法很少用（99%用不到），所以本专栏博客不对其进行讲解。如果对稠密图和稀疏图的概念和构造还不清楚，可以参考Dijkstra求最短路篇一(全网最详细讲解两种方法，适合小白)(python，其他语言也适用)(超简单的邻接矩阵的构建)和Dijkstra求最短路篇二(全网最详细讲解两种方法，适合小白)(python，其他语言也适用)(超简单的邻接表的构建)

题目

题目链接：858. Prim算法求最小生成树

给定一个 $n$ 个点 $m$ 条边的无向图，图中可能存在重边和自环，边权可能为负数。
求最小生成树的树边权重之和，如果最小生成树不存在则输出 impossible。
给定一张边带权的无向图 $G=(V,E)$，其中 $V$ 表示图中点的集合，$E$ 表示图中边的集合，$n=|V|$，$m=|E|$。
由 $V$ 中的全部 $n$ 个顶点和 $E$ 中 $n-1$ 条边构成的无向连通子图被称为 $G$ 的一棵生成树，其中边的权值之和最小的生成树被称为无向图 $G$ 的最小生成树。

输入格式
第一行包含两个整数 $n$ 和 $m$。
接下来 $m$ 行，每行包含三个整数 $u,v,w$，表示点 $u$ 和点 $v$ 之间存在一条权值为 $w$ 的边。

输出格式
共一行，若存在最小生成树，则输出一个整数，表示最小生成树的树边权重之和，如果最小生成树不存在则输出 impossible。

数据范围
$1\le n\le 500,$
$1\le m\le 10^5,$
图中涉及边的边权的绝对值均不超过 $10000$。

输入样例

4 5
1 2 1
1 3 2
1 4 3
2 3 2
3 4 4

输出样例

6

Prim算法

   Prim 算法干的事情是：给定一个无向图，在图中选择若干条边把图的所有节点连起来。要求边长之和最小。在图论中，叫做求最小生成树。

   Prim 算法采用的是一种贪心的策略。

   每次将离连通部分的最近的点和点对应的边加入的连通部分，连通部分逐渐扩大，最后将整个图连通起来，并且边长之和最小。

   我们将图中各个节点用数字 1 ~ n 编号。

要将所有景点连通起来，并且边长之和最小，步骤如下：

1. 用一个 state 数组表示节点是否已经连通。state[i] 为真，表示已经连通，state[i] 为假，表示还没有连通。初始时，state 各个元素为假。即所有点还没有连通。
   用一个 dist 数组保存各个点到连通部分的最短距离，dist[i] 表示 i 节点到连通部分的最短距离。初始时，dist 数组的各个元素为无穷大。
   用一个 pre 数组保存节点的是和谁连通的。pre[i] = k 表示节点 i 和节点 k 之间需要有一条边。初始时，pre 的各个元素置为 -1(初始值不在1~n号点之间都可以)。

2. 从 1 号节点开始扩充连通的部分，所以 1 号节点与连通部分的最短距离为 0，即disti[1] 置为 0。

3. 遍历 dist 数组，找到一个还没有连通起来，但是距离连通部分最近的点，假设该节点的编号是 i。i节点就是下一个应该加入连通部分的节点，stata[i] 置为 1。
   用青色点表示还没有连通起来的点，红色点表示连通起来的点。
   这里青色点中距离最小的是 dist[1]，因此 state[1] 置为 1。
   

4. 遍历所有与 i 相连但没有加入到连通部分的点 j，如果 j 距离连通部分的距离大于 i j 之间的距离，即 dist[j] > num[i][j]（num[i][j] 为 i j 节点之间的距离），则更新 dist[j] 为 num[i][j]。这时候表示，j 到连通部分的最短方式是和 i 相连，因此，更新pre[j] = i。
   与节点 1 相连的有 2， 3， 4 号节点。1->2 的距离为 100，小于 dist[2]，dist[2] 更新为 100，pre[2] 更新为1。1->4 的距离为 140，小于 dist[4]，dist[4] 更新为 140，pre[2] 更新为1。1->3 的距离为 150，小于 dist[3]，dist[3] 更新为 150，pre[3] 更新为1。

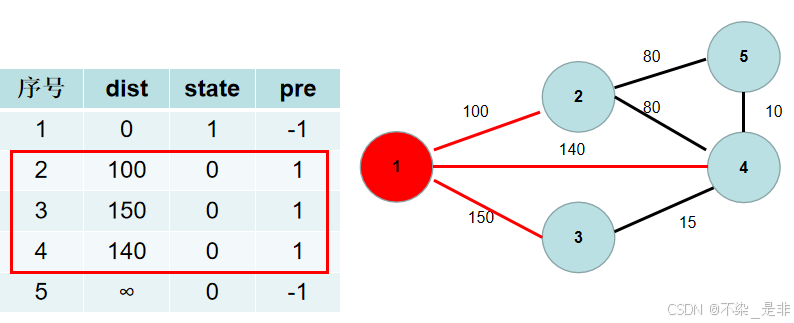
5. 重复 3 4步骤，直到所有节点的状态都被置为 1.
这里青色点中距离最小的是 dist[2]，因此 state[2] 置为 1。

与节点 2 相连的有 5， 4号节点。2->5 的距离为 80，小于 dist[5]，dist[5] 更新为 80，pre[5] 更新为 2。2->4 的距离为 80，小于 dist[4]，dist[4] 更新为 80，pre[4] 更新为2。

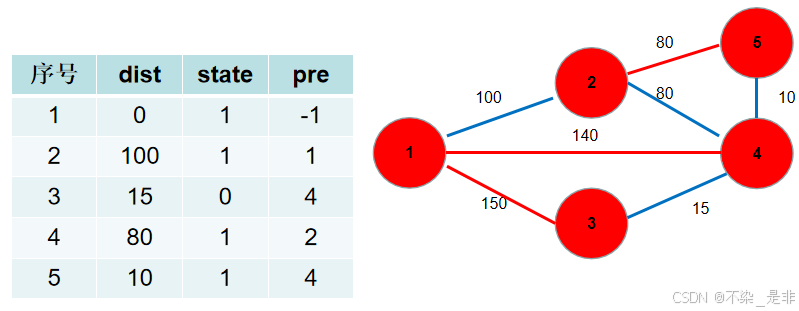
选dist[4]，更新dist[3]，dist[5]，pre[3]，pre[5]。

选dist[5]，没有可更新的。

选dist[3]，没有可更新的。

6. 此时 dist 数组中保存了各个节点需要修的路长，加起来就是。pre 数组中保存了需要选择的边。

详细代码

n, m = map(int, input().split())
num = [[float('inf') for i in range(n + 1)] for j in range(n + 1)]  # 用邻接矩阵存储图
for i in range(m):
    a, b, w = map(int, input().split())
    # 因为是无向图，所以a到b和b到a的权重是一样的，并且取两者中的较小值
    num[a][b] = num[b][a] = min(num[a][b], w)   
    
dist = [float('inf')] * (n + 1)  # 存储各个节点到生成树的距离
dist[1] = 0                      # 从 1 号节点开始生成 
# 初始化一个数组state，用于标记各个节点是否已经被加入到最小生成树中，初始值都为False
state = [False] * (n + 1)  
# 初始化一个数组pre，用于记录最小生成树中每个节点的前驱节点，方便最后输出路径，初始值都为-1
pre = [-1] * (n + 1)   # 节点的前驱节点

def prim():
    res = 0 
    for i in range(n):  # 每次循环选出一个点加入到生成树
        t = -1	  # 初始化选择的节点为-1，表示还没有选择
        #   遍历所有节点，找出距离最小生成树最近的且还未被加入的节点
        for j in range(1, n + 1):  
            if (not state[j]) and (t == -1 or dist[t] > dist[j]):   # 如果没有在树中，且到树的距离最短，则选择该点
                t = j
        # 如果找到的最短距离仍然是正无穷大，说明存在孤立点，无法形成最小生成树
        if dist[t] == float('inf'):
            print('impossible')
            return
        # 将找到的节点t加入到最小生成树中，并累加其权重到结果中
        res += dist[t]
        state[t] = True  # 把该节点加入到生成树中
        for j in range(1, n + 1):   # 更新生成树外的点到生成树的距离
            if dist[j] > num[t][j] and not state[j]:    # 从 t 到节点 j 的距离小于原来距离（且j不在生成树中），则更新。
                dist[j] = num[t][j]     # 更新距离
                pre[j] = t  # 从 t 到 j 的距离更短，j 的前驱变为 t.
    # 输出最小生成树的总权重
    print(res)

prim()  # 求最小生成树
# 下面的代码是可选的，用于输出最小生成树的路径（从节点1到所有其他节点的路径）
# 但由于题目没有要求输出路径，所以这部分代码被注释掉了
# for i in range(n , 0, -1):    # 从n到1逆序输出，因为是从1开始的编号
#     print(i, pre[i])		# 输出当前节点和它的前驱节点