自注意力机制 SANS

前言

---

在自然语言处理（NLP）的广阔天地里，seq2seq模型架构（即将一个序列映射到另一个序列）犹如一颗璀璨的明星，自2013至2014年间由多位研究先驱携手点亮，尤其在机器翻译领域大放异彩。随后，attention机制的引入更是为seq2seq模型锦上添花，这一强强联合的组合几乎成为了众多任务的制胜法宝。只需提供充足的输入输出对，通过精心构建两端的序列模型与attention机制，便能培育出一个性能不俗的模型。seq2seq的魔力不仅限于机器翻译，它还广泛渗透于文本生成的诸多场景，如文本摘要、代码自动补全、诗词创作等，其核心理念更是跨越了文本界限，向语音和图像领域延伸，展现出无限的应用潜力。

那么在transfromers前传统的seq2seq任务实现方案是如何是实现的，有哪些缺点呢？

传统的序列模型通常使用的是循环神经网络，如RNN（或者LSTM，GRU等），但是循环神经网络的计算限制为是顺序的，也就是说循环神经网络算法只能从左向右依次计算或者从右向左依次计算，这种机制带来了三个问题：

1. 时间片 t 的计算依赖 t−1 时刻的计算结果，需要计算完前一个时间刻才能下一步计算这样限制了模型的并行能力；比如RNN中的t0时刻跟t10时刻的信息如果要交互，必须经过t1~t9，才能传递过去，信息且会随着传递距离增加而衰减，对信息的捕获能力较差，所求特征的表征能力也就更差了

2. 传统的序列模型存在着长期依赖问题，难以捕捉长距离的依赖关系。顺序计算的过程中信息会丢失，尽管LSTM等门机制的结构一定程度上缓解了长期依赖的问题，但是对于特别长期的依赖现象, LSTM依旧无能为力。而如果用CNN来代替RNN的解决方法（平行化)，但也只能感受到部分的感受野，需要多层叠加才能感受整个图像，其中可以参考下图辅助理解。
   
   为了解决这个问题，作者提出一种新的注意力机制 self attention 结构，我们下面就看提出的这种结构如何解决上面的两个问题

Self Attention

---

Self Attention是Transformer模型的灵魂核心组件之一。该机制目的是让模型根据输入序列中不同位置的相关性权重来计算每个位置的表示，通过计算查询和键之间的相似性得分，并将这些得分应用于值来获取加权和，从而生成每个位置的输出表示。（其目的就是解决以上所说的两个问题）

这样我们在每个位置的序列输出都和全部位置的序列有关，这解决了第一个问题：全局的视野（对信息的捕获能力更强），同时该计算是各个向量矩阵点积运算，可以满足并行化运行，这就解决了第二个问题：时间片 t 的计算不依赖 t−1 时刻的计算结果，比如RNN中的t0时刻跟t10时刻的信息距离只是一个常量。

Self Attention接受的输入是三个相同的向量，分别命名为 Query 向量，一个 Key 向量和一个 Value 向量。

那我们面对输入序列X，如何满足Self Attention接受的输入呢？`

Q、K和V是通过对输入序列进行线性变换得到的，通过对输入序列的每个位置应用不同的权重矩阵，将输入序列映射到具有不同维度的查询（Q）、键（K）和值（V）空间。这样，我们就可以使用这些查询、键和值来输入到Self Attention结构计算注意力权重并生成加权表示。

给定一个输入序列X，我们可以通过线性变换得到Q、K和V：

Q = X * W_Q
K = X * W_K
V = X * W_V

其中W_Q、W_K和W_V是可学习的权重矩阵。

使用Q、K和V的好处是，它们允许模型根据输入的不同部分对相关信息进行加权。Q用于查询输入序列的每个位置，K用于提供关于其他位置的信息，V则提供用于计算加权表示的值。

值（V）代表的是确切的值（线性变换得到），一般是不变的用于求最后的输出，其次要实现求各个向量的相似性，如果只有一个k，而没有q，那k 与其他输入的 k作相似性，自己单元没有可以做相似性的地方，而再加一个q就可以实现了, 从而最后得到权重。

在第一次看到Q,K,V的时候我们会想，为什么需要这三个值呢？`

Self Attention 为了解决以上所说的两个问题，所采取的思路是通过全局位置的序列向量之间的相似性关系进行建模，来达到全局视野的目的，那么我们要计算每个位置向量之间的相似性权重，并指导当前位置的输出。

一种常用的计算相似度的方法是点积运算，而 Q,K 向量点击运算的结果每个位置向量之间（包括自己与自己）的相似性权重，而V则是与注意力权重用于当前位置的输出。

QK是专门用于求相似性的，如果只有一个向量比如k，而没有q，k 可以与其他位置向量的 k作相似性，但在自己单元却没有可以做相似性的地方，此时就无法进行各个相似性关系的比较从而得到关于全局位置的输出了，要解决该问题而再加一个向量q就可以实现了。

Self Attention 具体的流程图如下：

我们先看图片所示$a^1$的例子，首先将$a^1$的$q^1$与所有时间刻的$k^1$ 进行inner product并除与($\sqrt{d_k}$)( 其中$d_k$)是Q和K的维度。计算二者的相似性，得到 对应的相似性序列值$a_{1,i}$

为什么需要除与维度长度的根号呢？

这是因为当数据维度值越大时，inner product的结果越大，通过将Q和K进行点积操作并除以
($\sqrt{d_k}$)来缩放注意力权重，这有助于减小梯度在计算注意力时的变化范围（维度越大值越大），使得训练更加稳定。

对相似性序列值 $a_{1,i}$ 进行 Softmax 操作得到每个时刻的相似性权重

而后通过对每个时间刻的相似性权重和Value向量点积累加，最终得到 $a^1$所对应的 $b^1$

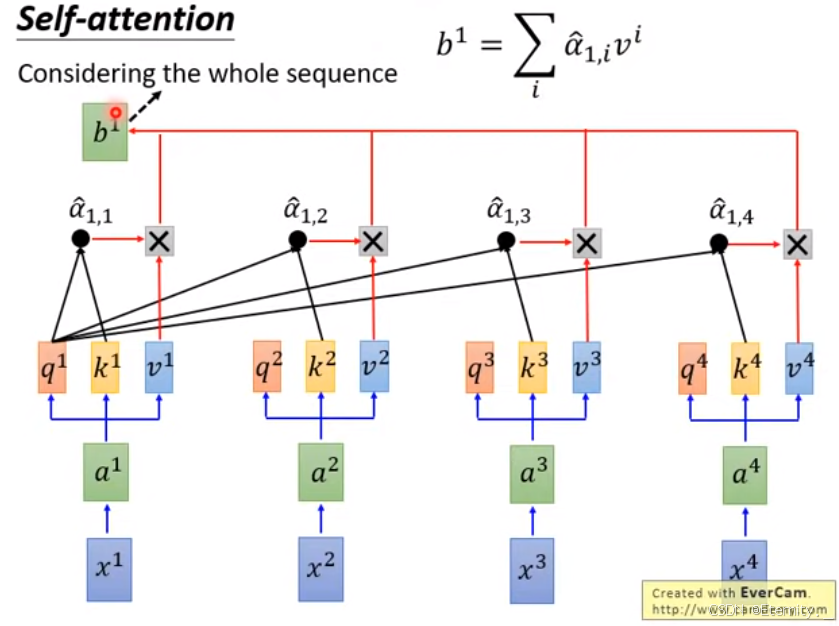
以此类推计算不同位置对应的$b_i$输出 序列 b，我们可以得到矩阵相乘的式子，从而一次计算出所有时刻的输出，这样便实现了平行化计算（矩阵运算），计算过程如下图所示

这样我们就最终得到Self Attention 公式如下：

$$\text{Attention}(Q,K,V)=\text{softmax}\left({\left(d_k\right)}^{-\frac{1}{2}}Q{K}^T\right)\cdot V$$

使用方式

---

依赖
Python 3.5
Keras

代码实现（Keras实现，结论：在这个经典的imdb数据集上的表现，只是中等。原因大致是该架构比较复杂，模型拟合需要更多的数据和轮次）

训练运行： python imdb_attention.py （self attention)
还可以运行其他模型

结论

---

(Transformer, 即多头自注意力) 在这个经典的小文本分类数据集上的表现，只是中等。

---