你会喜欢什么样的活动?人们很自然地会通过你的邻居来推测你的喜好。这正是KNN(K-Nearest Neighbors)算法的核心思想——“近朱者赤,近墨者黑”。
一、KNN基本思想
KNN(K Nearest Neighbors)是一种惰性学习(lazy learning) 算法,因为它不会对训练数据进行显式的学习或建模,只是把训练数据存储起来,直到测试阶段才进行计算,通过计算未知样本与训练集中所有样本的"距离",找出最相似的K个邻居,根据这些邻居的类别来决定未知样本的类别。
KNN不仅适用于分类问题,也可用于回归问题,两者的处理流程相似但目标不同:
| 任务类型 | 目标 | 决策方式 |
|---|---|---|
| 分类 | 预测类别标签 | 多数表决 |
| 回归 | 预测连续数值 | 取K个邻居的平均值 |
- 计算未知样本到每个训练样本的距离
- 按距离升序排列
- 取前K个最近邻
分类流程:
- 统计K个邻居中各类别出现次数
- 将未知样本归为出现次数最多的类别
回归流程:- 计算K个邻居目标值的平均值
- 将平均值作为预测值
二、Scikit-learn中的KNN API
Scikit-learn提供了KNeighborsClassifier(分类)和KNeighborsRegressor(回归)两个核心类。
1. 分类器 KNeighborsClassifier
from sklearn.neighbors import KNeighborsClassifier
# 创建KNN分类器实例
knn_clf = KNeighborsClassifier(
n_neighbors=5, # K值,默认5
weights='uniform', # 投票权重:'uniform'(等权重)或 'distance'(按距离反比加权)
algorithm='auto', # 最近邻算法:'auto', 'ball_tree', 'kd_tree', 'brute'
p=2, # 距离度量参数:p=1(曼哈顿距离),p=2(欧氏距离)
metric='minkowski', # 距离度量标准,默认为闵可夫斯基距离
n_jobs=None # 并行计算:None用1个核心,-1用所有核心
)
关键参数详解:
n_neighbors(K值):选择最近的邻居数量。K值过小模型容易过拟合,对噪声敏感;K值过大模型可能欠拟合,决策边界平滑。weights:权重函数。'uniform'表示所有近邻权重相等;'distance'则表示距离越近的邻居权重越大,这在处理不平衡数据或希望更强调近距离样本时很有效。algorithm:计算最近邻的算法。对于高维数据,'ball_tree'或'kd_tree'通常比暴力搜索('brute')更高效。p和metric:共同定义距离度量。
metric='minkowski'且p=1:曼哈顿距离metric='minkowski'且p=2:欧氏距离(默认)- 其他可选的
metric还包括'cosine'(余弦相似度)等。
2. 回归器 KNeighborsRegressor
from sklearn.neighbors import KNeighborsRegressor
# 创建KNN回归器实例
knn_reg = KNeighborsRegressor(
n_neighbors=5,
weights='uniform',
algorithm='auto',
p=2,
metric='minkowski'
)
回归器的参数与分类器基本一致,其
weights参数同样支持'uniform'和'distance'。
3. 通用方法
创建分类器或回归器对象后,使用方法是一致的:
# 拟合模型(实际是存储训练数据)
knn_model.fit(X_train, y_train)
# 进行预测
y_pred = knn_model.predict(X_test)
# 对于分类器,还可以获取预测概率(返回每个类别的概率)
# y_proba = knn_clf.predict_proba(X_test)
三、KNN算法核心——六大距离度量
1、欧氏距离(Euclidean Distance)
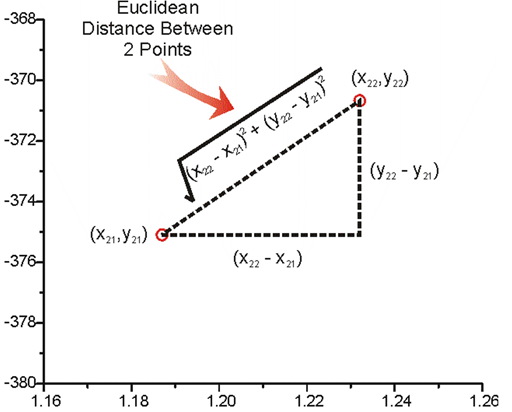
数学定义
distance=∑i=1n(xi−yi)2\text{distance} = \sqrt{\sum_{i=1}^{n}(x_i - y_i)^2}distance=i=1∑n(xi−yi)2
核心特点:
- 几何解释:多维空间中的直线距离
- 最佳场景:低维连续数据(<100维)
- 算法表现:在物理空间数据上表现优异
# Python实现
import numpy as np
def euclidean_distance(x, y):
return np.sqrt(np.sum((x - y)**2))
# Scikit-learn应用
from sklearn.neighbors import KNeighborsClassifier
knn = KNeighborsClassifier(metric='euclidean')
2、曼哈顿距离(Manhattan Distance)
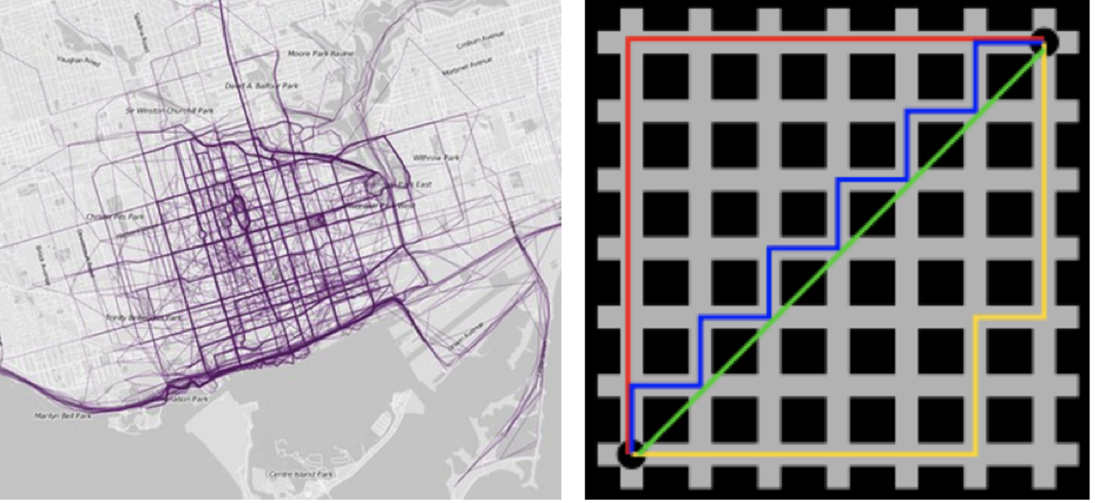
数学定义
distance=∑i=1n∣xi−yi∣\text{distance} = \sum_{i=1}^{n}|x_i - y_i|distance=i=1∑n∣xi−yi∣
核心特点:
- 几何解释:网格路径距离(城市街区距离)
- 最佳场景:高维数据(>100维)和离散特征
- 算法优势:对维度膨胀不敏感
# Python实现
def manhattan_distance(x, y):
return np.sum(np.abs(x - y))
# Scikit-learn应用
knn = KNeighborsClassifier(metric='manhattan')
3、切比雪夫距离(Chebyshev Distance)
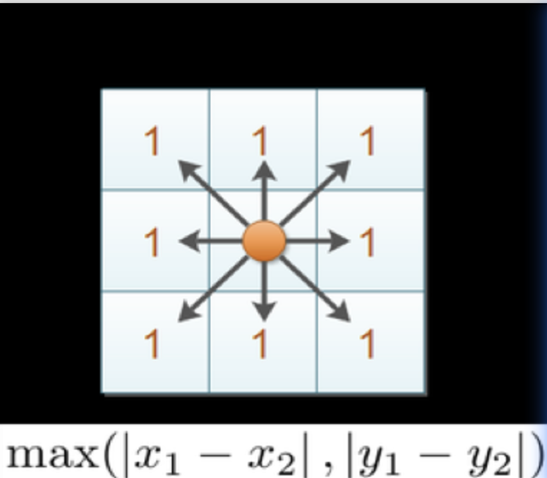
数学定义
distance=max(∣xi−yi∣)\text{distance} = \max(|x_i - y_i|)distance=max(∣xi−yi∣)
核心特点:
- 几何解释:各维度最大差值
- 最佳场景:棋盘游戏、等方性移动
- 算法特性:只关注最大差异维度
# Python实现
def chebyshev_distance(x, y):
return np.max(np.abs(x - y))
# Scikit-learn应用
knn = KNeighborsClassifier(metric='chebyshev')
4、闵可夫斯基距离(Minkowski Distance)
数学定义
distance=(∑i=1n∣xi−yi∣p)1/p\text{distance} = \left( \sum_{i=1}^{n}|x_i - y_i|^p \right)^{1/p}distance=(i=1∑n∣xi−yi∣p)1/p
参数控制:
- p=1p=1p=1 → 曼哈顿距离
- p=2p=2p=2 → 欧氏距离
- p→∞p\to\inftyp→∞ → 切比雪夫距离
# Scikit-learn应用
knn = KNeighborsClassifier(
metric='minkowski',
p=2 # 可调参数
)
5. 余弦相似度(Cosine Similarity)
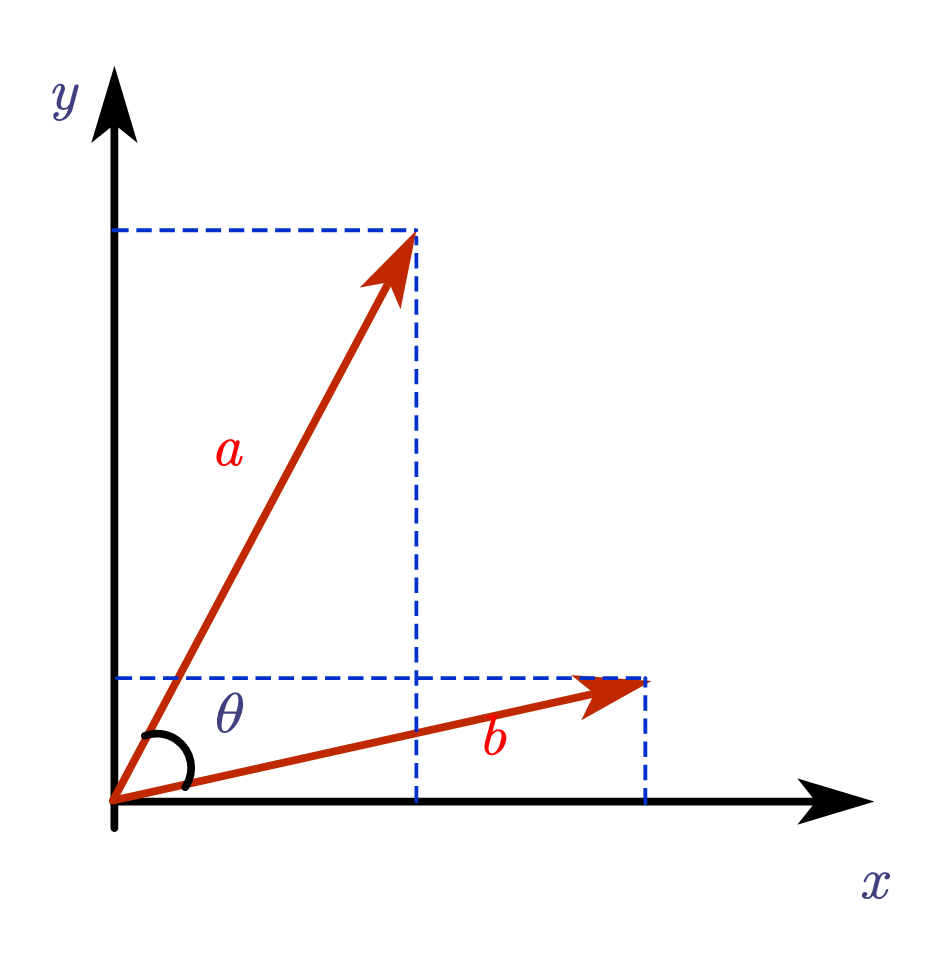
数学定义
计算公式:
cosine_similarity=A⋅B∥A∥∥B∥=∑i=1nAiBi∑i=1nAi2∑i=1nBi2\text{cosine\_similarity} = \frac{\mathbf{A} \cdot \mathbf{B}}{\|\mathbf{A}\| \|\mathbf{B}\|} = \frac{\sum_{i=1}^{n}A_i B_i}{\sqrt{\sum_{i=1}^{n}A_i^2} \sqrt{\sum_{i=1}^{n}B_i^2}}cosine_similarity=∥A∥∥B∥A⋅B=∑i=1nAi2∑i=1nBi2∑i=1nAiBi
几何意义:测量两个向量在多维空间中的方向一致性,完全忽略向量长度(模长)
核心特性:
- 值域范围:[-1, 1]
- 不变性:对向量长度变化不敏感(仅关注方向)
- 最优场景:高维稀疏数据(如文本TF-IDF向量)
from sklearn.metrics.pairwise import cosine_similarity
from sklearn.neighbors import KNeighborsClassifier
# 直接计算
text_vector1 = [0.8, 0.3, 0, 0, 0.5]
text_vector2 = [0.7, 0.4, 0, 0, 0.6]
similarity = cosine_similarity([text_vector1], [text_vector2])
print(f"余弦相似度: {similarity[0][0]:.3f}")
# 在KNN中的应用
knn_text = KNeighborsClassifier(
metric='cosine', # 关键参数
n_neighbors=5
)
knn_text.fit(X_train_tfidf, y_train)
6. 汉明距离(Hamming Distance)
数学定义
计算公式:
hamming_distance=∑i=1n1Ai≠Bi\text{hamming\_distance} = \sum_{i=1}^{n} \mathbb{1}_{A_i \neq B_i}hamming_distance=i=1∑n1Ai=Bi
几何意义:统计两个等长字符串在相应位置上不同字符的个数
核心特性:
- 适用前提:两个比较序列必须等长
- 计算效率:O(n)时间复杂度,极高计算效率
- 最优场景:二进制数据、遗传序列、错误检测
from scipy.spatial.distance import hamming
from sklearn.neighbors import KNeighborsClassifier
# 直接计算
seq1 = [1, 0, 1, 0, 1, 0]
seq2 = [1, 0, 0, 1, 1, 0]
distance = hamming(seq1, seq2)
print(f"汉明距离: {distance:.3f}") # 2/6=0.333
# 在KNN中的应用
knn_dna = KNeighborsClassifier(
metric='hamming', # 关键参数
n_neighbors=3
)
knn_dna.fit(X_dna_sequences, y_labels)
7、使用场景
| 数据类型 | 推荐距离 | Scikit-learn参数 | 案例 |
|---|---|---|---|
| 低维连续数据 | 欧氏距离 | metric='euclidean' | 鸢尾花分类 |
| 高维数据 | 曼哈顿距离 | metric='manhattan' | 手写数字识别 |
| 网格移动 | 切比雪夫距离 | metric='chebyshev' | 棋盘游戏AI |
| 需要调参 | 闵可夫斯基距离 | metric='minkowski', p=值 | 综合实验 |
| 文本数据 | 余弦相似度 | metric='cosine' | 文档分类 |
| 二进制数据 | 汉明距离 | metric='hamming' | 基因序列匹配 |
四、特征预处理——标准化 & 归一化
KNN算法基于距离计算,因此对特征的尺度非常敏感。较大尺度的特征会在距离计算中占据主导地位。必须进行特征缩放。
- 标准化 (StandardScaler):将数据转换为均值为0,标准差为1的分布。对异常值不敏感,适合大多数场景。
- 归一化 (MinMaxScaler):将数据缩放到一个指定的范围(默认[0, 1])。对异常值敏感。
1、归一化(Min-Max Scaling)
归一化通过对原始数据进行线性变换,将数据映射到[0, 1]区间(可自定义范围)。计算公式:
Xnorm=X−μσX_{\text{norm}} = \frac{X - \mu}{\sigma}Xnorm=σX−μ
特点:
- 对异常值敏感(极值影响全局)
- 输出范围固定
- 适合传统小数据场景
Python实现:
from sklearn.preprocessing import MinMaxScaler
data = [[90, 2, 10, 40],
[60, 4, 15, 45],
[75, 3, 13, 46]]
scaler = MinMaxScaler(feature_range=(0, 1)) # 默认[0,1]
scaled_data = scaler.fit_transform(data)
print(scaled_data)
# 输出:
# [[1. 0. 0. 0. ]
# [0. 1. 1. 0.83333333]
# [0.5 0.5 0.6 1. ]]
2、标准化(Z-Score Scaling)
标准化基于正态分布,将数据转换为均值为0、标准差为1的标准正态分布。计算公式:
Xstd=X−μσX_{\text{std}} = \frac{X - \mu}{\sigma}Xstd=σX−μ
特点:
- 对异常值稳健(少量异常点影响有限)
- 输出范围不固定
- 适合现代大数据场景(推荐首选)
Python实现:
from sklearn.preprocessing import StandardScaler
data = [[90, 2, 10, 40],
[60, 4, 15, 45],
[75, 3, 13, 46]]
scaler = StandardScaler()
scaled_data = scaler.fit_transform(data)
print(scaled_data)
# 输出:
# [[ 1.22474487 -1.22474487 -1.29777137 -1.3970014 ]
# [-1.22474487 1.22474487 1.13554995 0.50800051]
# [ 0. 0. 0.16222142 0.88900089]]
3、选择场景
| 场景 | 推荐方法 | 原因 |
|---|---|---|
| 数据分布未知 | 标准化 | 不假设分布 |
| 存在异常值 | 标准化 | 对异常值不敏感 |
| 需要固定输出范围(如GAN) | 归一化 | 结果严格在[0,1]区间 |
| 数据符合均匀分布 | 归一化 | 保持原始分布特性 |
使用场景不明晰时推荐使用标准化:
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import make_pipeline
# 创建包含标准化的KNN管道
pipeline = make_pipeline(
StandardScaler(), # 第一步:标准化
KNeighborsClassifier(n_neighbors=5) # 第二步:KNN分类
)
# 使用管道训练和预测(自动处理缩放)
pipeline.fit(X_train, y_train)
accuracy = pipeline.score(X_test, y_test)
- 注意:测试集必须使用训练集的缩放参数进行转换,以避免数据泄露,使用
pipeline或StandardScaler的transform方法可以自动保证这一点。- make_pipeline的使用非常简单,你只需要按顺序传入各个步骤的转换器(Transformer,如 StandardScaler)和估计器(Estimator,如 KNeighborsClassifier)的实例即可。最后一个步骤通常是估计器(模型)
五、超参数调优——交叉验证与网格搜索
K值的选择是KNN算法中的关键超参数,它直接影响模型表现:
K值过小(如K=1):
- 模型过于敏感,容易学习到噪声
- 易受异常点影响
- 可能导致过拟合
K值过大(如K=训练样本数):
- 模型过于简单,忽略局部特征
- 预测结果偏向多数类
- 可能导致欠拟合
比喻: 选择K值就像选择朋友圈的大小:
- 朋友圈太小(K小):容易受个别人影响,判断偏激
- 朋友圈太大(K大):忽略个性,只随大流
手动选择K值等超参数很困难。通常使用网格搜索(GridSearchCV) 结合交叉验证(Cross-Validation) 来寻找最优参数。
交叉验证(Cross-Validation)是一种数据集的分割方法,将训练集划分为 n 份,拿一份做验证集(测试集)、其他n-1份做训练集 。
为什么需要交叉验证:单一的训练-测试分割可能导致评估结果不稳定(受随机分割影响)。交叉验证通过多次数据分割,提供更稳健的模型评估。
K折交叉验证流程:
- 划分训练集:将训练集均分为K份
- 模型训练:每次用1份作为验证集,其余K-1份作为训练集
- 模型评估:重复K次训练和评估
- 选出最佳组合:取K次结果的平均值作为最终评估
网格搜索(GridSearch)是一种超参数优化技术,用于系统地遍历多个超参数组合,以找到最优的超参数配置,从而提升模型性能,通过定义参数候选值的网格,遍历所有可能的组合,选择交叉验证评分最高的配置。
为什么需要网格搜索:模型有很多超参数,其能力也存在很大的差异。手动调参过程繁杂且效率低下。网格搜索通过穷举所有可能的参数组合,并采用交叉验证进行评估,可以自动找到最佳参数组合。
网格搜索核心流程:
- 定义参数网格:指定希望调整的参数及其可能取值的范围。
- 遍历组合:网格搜索会生成所有可能的超参数组合。
- 模型评估:对于每一组超参数组合,使用交叉验证评估模型性能。
- 选出最佳组合:基于交叉验证的评估结果,选择使得模型性能最优的超参数组合。
api解读
GridSearchCV 是 Scikit-learn 中实现网格搜索和交叉验证的核心类。
主要参数
| 参数名 | 说明 |
|---|---|
estimator | 指定要调优的模型对象(例如 KNeighborsClassifier()) |
param_grid | 一个字典或列表,指定需要搜索的超参数及其候选值范围 |
cv | 指定交叉验证的折数或策略,例如 cv=5 表示 5 折交叉验证 |
scoring | 模型评估指标,如 'accuracy'(默认)、'f1'、'precision' 等 |
n_jobs | 并行运行的作业数。-1 表示使用所有可用的处理器 |
verbose | 控制输出信息的详细程度。数值越大,信息越详细 |
常用属性
在调用 fit 方法之后,你可以通过以下属性获取网格搜索的结果:
| 属性名 | 说明 |
|---|---|
best_params_ | 返回在交叉验证中验证的最佳参数组合 |
best_score_ | 返回最佳参数组合在交叉验证中得到的平均分数 |
best_estimator_ | 返回使用最佳参数训练好的最终模型 |
cv_results_ | 返回一个字典,包含网格搜索过程中所有参数组合的详细结果 |
六、鸢尾花案例实战(KNeighborsClassifier)
1、数据集介绍:鸢尾花分类
鸢尾花(Iris)数据集是机器学习领域最经典的数据集之一,由统计学家 R.A. Fisher 于 1936 年在其开创性论文中首次使用,用于展示线性判别分析方法。该数据集包含了三种鸢尾花(Setosa、Versicolour 和 Virginica)各 50 个样本,共 150 个样本,每个样本测量了 4 个特征。
| 特性 | 描述 |
|---|---|
| 样本数 | 150 (每类各 50) |
| 特征数 | 4 个数值特征 |
| 目标变量 | 鸢尾花种类 (Setosa, Versicolour, Virginica) |
| 特征含义 | 花萼长度 (cm)、花萼宽度 (cm)、花瓣长度 (cm)、花瓣宽度 (cm) |
核心特点与挑战:
- 数据质量高:数据集非常干净,通常没有缺失值。
- 特征相关性:花瓣长度和花瓣宽度与类别标签有很高的相关性(分别可达 0.9490 和 0.9565),是区分物种的关键特征。
- 类别可分性:Setosa 类与其他两类是线性可分的,而 Versicolour 和 Virginica 两类之间是非线性可分的。这为测试不同分类算法的能力提供了很好的场景。
1、基础版
# 1. 导入必要的库
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import accuracy_score
# 2. 加载数据
iris = load_iris()
X = iris.data # 特征矩阵 (150, 4)
y = iris.target # 目标标签 (150,)
# 3. 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(
X, y,
test_size=0.2, # 20%的数据作为测试集
random_state=42 # 随机种子,确保结果可复现
)
# 4. 创建并训练KNN模型(选择3个邻居)
knn = KNeighborsClassifier(n_neighbors=3)
knn.fit(X_train, y_train)
# 5. 在测试集上进行预测并评估准确率
y_pred = knn.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)
print(f"KNN模型准确率: {accuracy:.2%}") # 通常可达96.67%以上
基础版核心要点:
- 数据获取:
load_iris()轻松加载数据。- 数据拆分:
train_test_split将数据分为训练集(用于模型学习)和测试集(用于评估模型未见过的数据时的性能)。- 模型选择与训练:
KNeighborsClassifier是一个简单直观的算法,适合入门。n_neighbors=3表示基于最近的3个样本进行投票决策。fit方法用于模型学习。- 评估:
accuracy_score计算模型预测正确的比例,是最直观的评估指标。
2、进阶版
# 1. 导入进阶工具库
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import make_pipeline
from sklearn.model_selection import GridSearchCV
from sklearn.metrics import classification_report, confusion_matrix
# 2. 创建包含数据预处理和模型的管道
# 管道确保标准化器只在训练数据上拟合,然后转换训练和测试数据,避免数据泄露。
pipe = make_pipeline(
StandardScaler(), # 第一步:标准化特征(减去均值,除以标准差)
KNeighborsClassifier() # 第二步:KNN分类器
)
# 3. 定义超参数网格进行调优
# 我们不猜测最佳参数,而是让GridSearchCV自动寻找。
param_grid = {
'kneighborsclassifier__n_neighbors': [1, 3, 5, 7, 9, 11],
'kneighborsclassifier__weights': ['uniform', 'distance'],
'kneighborsclassifier__p': [1, 2] # 1:曼哈顿距离, 2:欧氏距离
}
# 4. 设置网格搜索与交叉验证
# GridSearchCV会遍历所有参数组合,并使用5折交叉验证评估每一种组合的性能。
grid_search = GridSearchCV(
pipe,
param_grid,
cv=5, # 5折交叉验证
scoring='accuracy',
n_jobs=-1 # 使用所有CPU核心并行计算
)
# 5. 在训练集上执行网格搜索(自动找到最佳参数)
grid_search.fit(X_train, y_train)
# 6. 输出最佳参数和模型性能
print(f"最佳参数组合: {grid_search.best_params_}")
print(f"最佳交叉验证准确率: {grid_search.best_score_:.2%}")
# 7. 使用最佳模型在测试集上进行最终评估
best_model = grid_search.best_estimator_
y_pred_advanced = best_model.predict(X_test)
# 8. 全面的模型评估
print("\n=== 测试集性能评估 ===")
print(f"测试集准确率: {accuracy_score(y_test, y_pred_advanced):.2%}")
print("\n**详细分类报告:**")
print(classification_report(y_test, y_pred_advanced, target_names=iris.target_names))
print("\n**混淆矩阵:**")
print(confusion_matrix(y_test, y_pred_advanced))
进阶版核心要点:
- 特征标准化:
StandardScaler将特征数据缩放到均值为0、方差为1的标准正态分布。这一步至关重要,因为KNN等基于距离的算法对特征的尺度非常敏感。花瓣长度(单位是厘米)的数值可能远大于花瓣宽度(单位是厘米),如果不处理,模型会过于关注数值大的特征。- 管道(Pipeline):
make_pipeline将预处理步骤和估计器(模型)封装成一个整体。这有效避免了数据泄露(Data
Leakage),确保测试集的信息不会在训练时被用到。它也使得代码更加简洁和可重复。- 超参数调优与交叉验证:
GridSearchCV自动化地遍历我们给定的参数组合(param_grid),并对每一组参数使用交叉验证(本例中为5折,cv=5)来评估其性能。这比手动尝试不同参数并依赖单次
train-test split 要可靠得多,能帮助我们找到泛化能力更强的模型配置。- 全面评估:除了准确率,
classification_report提供了精确率(Precision)、召回率(Recall)、F1-score
等指标,可以更细致地评估模型在每个类别上的表现。confusion_matrix则清晰地展示了哪些类别容易被混淆。
七、加州房价案例实战(KNeighborsRegressor)
1、数据集介绍:加州房价
加州房价数据集包含1990年加州人口普查的区块数据,是预测房屋中位价的多元回归问题。
| 特性 | 描述 |
|---|---|
| 样本数 | 20,640 |
| 特征数 | 8个数值特征 |
| 目标变量 | 房屋中位价 (单位: 10万美元) |
| 特征含义 | 经度、纬度、房屋平均年龄、平均房间数、平均卧室数、人口、平均占用率、收入中位数 |
核心挑战: 特征尺度不一 (如经度与房间数),必须进行特征标准化。
2、基础版
# 最简版KNN回归预测加州房价
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsRegressor
from sklearn.metrics import mean_squared_error
# 1. 加载数据
X, y = fetch_california_housing(return_X_y=True)
# 2. 数据标准化
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
# 3. 划分数据集
X_train, X_test, y_train, y_test = train_test_split(X_scaled, y, test_size=0.2, random_state=42)
# 4. 训练模型
knn = KNeighborsRegressor(n_neighbors=5)
knn.fit(X_train, y_train)
# 5. 预测与评估
y_pred = knn.predict(X_test)
mse = mean_squared_error(y_test, y_pred)
print(f"模型MSE: {mse:.3f}")
print(f"测试集R²分数: {knn.score(X_test, y_test):.3f}")
基础版核心要点与输出:
- 标准化: KNN基于距离计算,必须使用
StandardScaler消除特征量纲影响。- 评估指标:
- RMSE (均方根误差): 越小越好,表示预测值与真实值的平均偏差。
- R² (决定系数): 越接近1越好,表示模型对目标变量变化的解释程度。
- 预期结果: 基础模型R²通常在0.6-0.7左右,有较大优化空间。
3、进阶版
# 进阶版KNN回归简化实现
import numpy as np
from sklearn.pipeline import Pipeline
from sklearn.model_selection import GridSearchCV
from sklearn.neighbors import KNeighborsRegressor
from sklearn.metrics import mean_squared_error, r2_score
# 1. 创建管道
pipe = Pipeline([
('scaler', StandardScaler()),
('knn', KNeighborsRegressor())
])
# 2. 定义参数网格
param_grid = {
'knn__n_neighbors': [3, 5, 7, 9],
'knn__weights': ['uniform', 'distance'],
'knn__p': [1, 2]
}
# 3. 网格搜索优化
grid_search = GridSearchCV(
pipe,
param_grid,
cv=5,
scoring='neg_mean_squared_error',
n_jobs=-1
)
grid_search.fit(X_train, y_train)
# 4. 评估最佳模型
best_model = grid_search.best_estimator_
y_pred = best_model.predict(X_test)
rmse = np.sqrt(mean_squared_error(y_test, y_pred))
r2 = r2_score(y_test, y_pred)
print(f"最佳参数: {grid_search.best_params_}")
print(f"RMSE: {rmse:.4f}")
print(f"R²: {r2:.4f}")
进阶版核心技术要点:
- 管道 (Pipeline): 将数据预处理(标准化)和模型训练封装成一个整体步骤,有效避免数据泄露,使代码更简洁、更可重现。
- 网格搜索与交叉验证 (GridSearchCV): 自动化地遍历给定的参数组合,并使用交叉验证来评估每一组参数的优劣,从而找到泛化能力最强的模型配置,取代了手动试错的低效方式。
- 特征分析: 通过可视化分析特征与目标变量的关系,例如收入中位数与房价通常呈现较强的正相关,这有助于理解模型和数据的本质。


























 5280
5280

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








