五道递归算法题--让你彻底爱上递归-CSDN博客

在解决一个规模为n的问题时，如果满足以下条件，我们可以使用递归来解决

问题可以被划分为规模更小的子问题，并且这些子问题具有与原问题相同的解决办法
当我们知道规模更小的子问题（规模为n-1）的解时，我们可以直接计算出规模为n的问题的解。
存在一种简单情况，或者说当问题的规模足够小时，我们可以直接求解问题。

一般的递归求解过程如下：

验证是否满足简单情况
假设较小规模的问题已经解决，解决当前问题。

如何写好一个递归

先找到相同的子问题->函数头的设计
只关心某一个子问题时如何解决的->函数体的书写
注意一下递归函数的出口--就是关心递归的结束条件

1.题目链接：面试题08.06.汉诺塔问题

1.2题目描述：

在经典汉诺塔问题中，有 3 根柱子及 N 个不同大小的穿孔圆盘，盘子可以滑入任意一根柱子。一开始，所有盘子自上而下按升序依次套在第一根柱子上(即每一个盘子只能放在更大的盘子上面)。移动圆盘时受到以下限制:
(1) 每次只能移动一个盘子;
(2) 盘子只能从柱子顶端滑出移到下一根柱子;
(3) 盘子只能叠在比它大的盘子上。

请编写程序，用栈将所有盘子从第一根柱子移到最后一根柱子。

你需要原地修改栈。

示例 1：

 输入：A = [2, 1, 0], B = [], C = []
 输出：C = [2, 1, 0]

示例 2：

 输入：A = [1, 0], B = [], C = []
 输出：C = [1, 0]

提示：

A 中盘子的数目不大于 14 个。

1.3解法(递归)

算法思路：
假设n = 1，只有一个盘子，很简单，直接把它从A中拿出来，移到C上；

如果n = 2呢？这时候我们就要借助B了，因为小盘子必须时刻都在大盘子上面，共需要3步(为了方便叙述，记A中的盘子从上到下为1号，2号)：

1号盘子放到B上；
2号盘子放到C上；
1号盘子放到C上；

至此，C中的盘子从上到下为1号，2号

如果n>2呢？这时我们需要用到n=2时的策略，将A上面除了最大的盘子，其余挪到B上，再将最大的盘子挪到C上，最后将B上的小盘子挪到C上就完成了所有步骤。

因为A中最后处理的是最大的盘子，所以在移动过过程中不存在大盘子在小盘子上面的情况。则本题可以被解释为：

对于规模为n的问题，我们需要将A柱上的n个盘子移动到C柱上
规模为n的问题可以被拆分为规模为n-1的子问题： a.将A柱上的上面n-1个盘子移动到B柱上； b.将A柱上最大的盘子移动到C柱上，然后将B柱上的n-1个盘子移动到C柱上。
当问题的规模变为n=1时，即只有一个盘子时，我们可以直接将其从A柱移动到C柱。

需要注意的是，步骤2.b考虑的是总体问题中的子问题b情况。在处理子问题时，我们应该将A柱中的最上面的盘子移动C柱，然后再将B柱上的盘子移动到C柱。在处理总体问题的子问题b时，A柱中的最大盘子仍然时最上面的盘子，因此这种做法时通用的。

1.4算法流程：

递归函数设计：void hanotaa(vector<int>& a, vector<int>& b, vector<int>& c,int n)

返回值：无；
参数：三个柱子上的盘子，当前需要处理的盘子个数(当前问题规模)。
函数作用：将a中的上面n个盘子挪到c中。

递归函数流程：

当前问题规模为n=1时，直接将a中的最上面的盘子挪到c中并返回；
递归将a中最上面的n-1个盘子挪到b中；
将a中最上面的一个盘子挪到c中；
将b中上面n-1个盘子挪到c中。

class Solution {
public:
    void hanota(vector<int>& a, vector<int>& b, vector<int>& c) {
        hannotaa(a,b,c,a.size());
    }

    void hannotaa(vector<int>& a, vector<int>& b, vector<int>& c,int num)
    {
    if(num == 1)
    {
        c.push_back(a.back());
        a.pop_back();
        return;
    }

        hannotaa(a,c,b,num-1);//a借助c放到b；
        c.push_back(a.back());
        a.pop_back();
        hannotaa(b,a,c,num-1);//b再将剩余的借助a放到b
    } 
};

2.题目链接：21.合并两个有序链表

2.2题目描述：

将两个升序链表合并为一个新的升序链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。

示例 1：

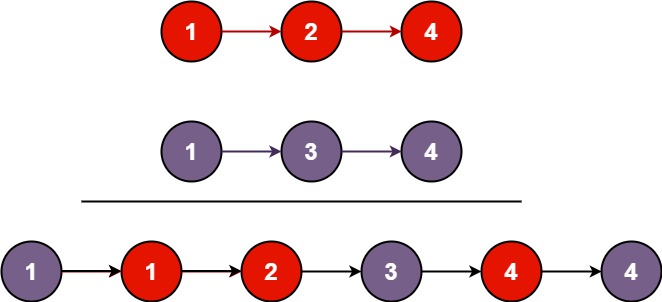
输入：l1 = [1,2,4], l2 = [1,3,4]
输出：[1,1,2,3,4,4]

示例 2：

输入：l1 = [], l2 = []
输出：[]

示例 3：

输入：l1 = [], l2 = [0]
输出：[0]

提示：

两个链表的节点数目范围是 [0, 50]
-100 <= Node.val <= 100
l1 和 l2 均按 非递减顺序 排列

2.3解法

算法思路：

递归函数的含义：交给你两个链表的头节点，你帮我把它们合并起来，并且返回合并后的头节点
函数体：选择两个头节点中较小的结点作为最终合并后的头节点，然后将剩下的链表交给递归函数去处理；
递归出口：当某一个链表为空的时候，返回另外一个链表

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {
        if(list1 == nullptr)return list2;
        if(list2 == nullptr)return list1;

        if(list1->val <= list2->val)
        {
            list1->next = mergeTwoLists(list1->next,list2);
            return list1;
        }
        else
        {
            list2->next = mergeTwoLists(list1,list2->next);
            return list2;
        }

    }
};

3.1题目链接：206.反转链表

3.2题目描述：

给你单链表的头节点 head ，请你反转链表，并返回反转后的链表。

示例 1：

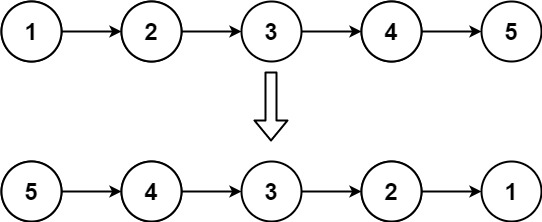
输入：head = [1,2,3,4,5]
输出：[5,4,3,2,1]

示例 2：

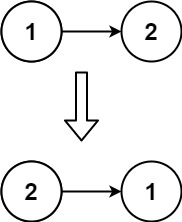
输入：head = [1,2]
输出：[2,1]

示例 3：

输入：head = []
输出：[]

提示：

链表中节点的数目范围是 [0, 5000]
-5000 <= Node.val <= 5000

3.3解法：

算法思路：

递归函数的含义：交给你一个链表的头指针，你帮我逆序之后，返回逆序后的头节点；
函数体：先把当前结点之后的链表逆序，逆序完之后，把当前结点添加到逆序后的链表后面
递归出口：当前结点为空或者当前只有一个结点的时候，不用逆序，直接返回。

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        //之所以结束条件不仅仅是head == nullptr，也是为了在递归中返回新的头节点做前序工作
        if(head == nullptr||head->next == nullptr)return head;

        ListNode* newhead = reverseList(head->next);//在递归中如何返回新的头节点。
        head->next->next = head;
        head->next = nullptr;
        return newhead;
    }
};

4.题目链接：24.两两交换链表中的结点

4.2题目描述：

给你一个链表，两两交换其中相邻的节点，并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题（即，只能进行节点交换）。

示例 1：

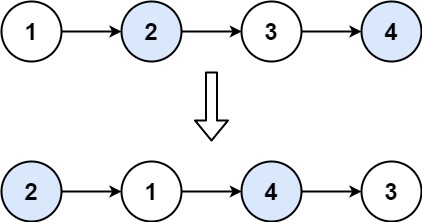
输入：head = [1,2,3,4]
输出：[2,1,4,3]

示例 2：

输入：head = []
输出：[]

示例 3：

输入：head = [1]
输出：[1]

提示：

链表中节点的数目在范围 [0, 100] 内
0 <= Node.val <= 100

4.3解法

算法思路：

递归函数的含义：交给你一个链表，将这个链表两两交换一下，然后返回交换后的头结点；
函数体：先去处理一下第二个结点往后的链表，然后再把当前的两个结点交换一下，连接上后面处理后的链表
递归出口：当前结点为空或者当前只有一个结点的时候，不用交换，直接返回。

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* swapPairs(ListNode* head) {
        if(head == nullptr ||head->next == nullptr)return head;

        ListNode* oldhead = swapPairs(head->next->next);
        ListNode* newhead = head->next;
        newhead->next = head;
        head->next = oldhead;
        return newhead;
    }
};

5.题目链接：50.Pow(x,n)

5.2题目描述：

实现 pow(x, n) ，即计算 x 的整数 n 次幂函数（即，xn ）。

示例 1：

输入：x = 2.00000, n = 10
输出：1024.00000

示例 2：

输入：x = 2.10000, n = 3
输出：9.26100

示例 3：

输入：x = 2.00000, n = -2
输出：0.25000
解释：2-2 = 1/22 = 1/4 = 0.25

提示：

-100.0 < x < 100.0
-2^31 <= n <= 2^31-1
n 是一个整数
要么 x 不为零，要么 n > 0 。
-10^4 <= xn <= 10^4

5.3解法(递归-快速幂)

算法思路：

递归函数的含义：求出x的n次方是多少，然后返回
函数体：先求出x的n/2次方是多少，然后根据n的奇偶，得出x的n次方是多少
递归出口：当n为0的时候，返回1即可

class Solution {
public:
    double myPow(double x,int n)
        {
        return n<0 ? 1.0/pow(x,-(long long)n):pow(x,n);
        }
    
    double pow(double x, long long n) {
        if(n==0)return 1.0;
        double tmp=pow(x,n/2);
        return n%2==0?tmp*tmp:tmp*tmp*x;
    }
};