【回溯法+动态规划】连续邮资问题——最佳邮票面值设计

前言

想象你是邮票设计师，如何指定n种面值使得1张信封上贴m枚邮票能“连续”贴出最大区间？这就是《连续邮资问题》。它结合了回溯和DP思想，是算法训练的好素材！

一、问题描述

国家要发行n种邮票，每封信最多贴m枚。请为n和m设计最佳面值，使得用1~m枚邮票能贴出的邮资连续区间最大。

举例说明：

• n=5,m=4，面值为(1,3,11,15,32)，区间是1~70。
• 而(1,6,10,20,30)只能贴出1-4，递增较慢。

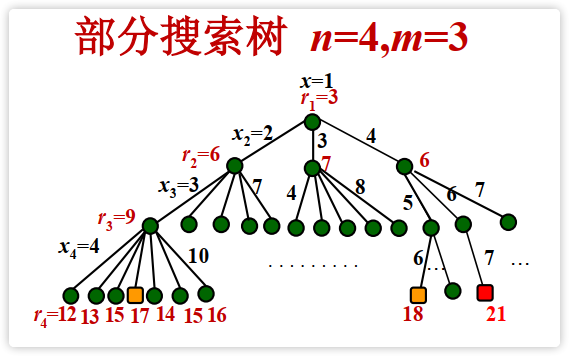
二、算法核心思路

1. 枚举组合（回溯法）
   用回溯法（深度优先搜索，DFS）枚举所有可能的面值组合。其中x1​必须等于1，其他面值按递增顺序枚举。每确定一组面值即可判定其最大连续区间。

2. 区间判定（动态规划） 对每一组面值，借助“完全背包”的动态规划计算最多可用m张邮票时，从1开始能拼出的最大连续邮资R。具体地，用一维数组y[k]表示拼出邮资k至少需要几张邮票。初始y[0]=0，其它为无穷大。对于每个邮票面值和每种邮票张数，尝试更新y[k]的最小张数。找到第一个k使得y[k]>m，则R=k−1。

3. 搜索空间剪枝优化 为加速搜索，常用经验剪枝，比如限制下一枚枚举的最大面值不超过当前最优解的最大R+一定常数，避免无效大枚举；并且面值严格递增，保证不重复。

4. 记录与更新最优解 持续更新当前已知的最优面值组合和对应最大连续区间R。

三、核心代码实现

#include <stdio.h>
#include <string.h>

#define N 10
#define MAXS 200
#define INF 10000

int n, m;
int bestx[N], x[N];
int maxR = 0;

/* 计算最大连续邮资区间 */
int calc_maxR(int *x, int n, int m)
{
    int y[MAXS+1];
    int i, j, k, r;

    for (i = 0; i <= MAXS; i++) y[i] = INF;
    y[0] = 0;
    for (i = 1; i <= m; i++)
        for (j = 1; j <= n; j++)
            for (k = MAXS; k >= x[j]; k--)
                if (y[k-x[j]] + 1 < y[k])
                    y[k] = y[k-x[j]] + 1;
    for (r = 1; r <= MAXS; r++)
        if (y[r] > m)
            break;
    return r-1;
}

void dfs(int t, int last)
{
    int v, r;
    if (t > n) {
        r = calc_maxR(x, n, m);
        if (r > maxR) {
            maxR = r;
            memcpy(bestx, x, sizeof(int)*(n+1));
        }
        return;
    }
    /* 必须适当放宽枚举上限，否很快剪死 */
    for (v = last+1; v <= maxR+30 && v <= MAXS; v++) { /* 30为经验值 */
        x[t] = v;
        /* 递归优化 (允许部分无进展递归, 若递归太少永远不产生新面值组合) */
        dfs(t+1, v);
    }
}

int main(void)
{
    int i;
    printf("请输入面值种类n, 信封最多贴票数m: ");
    scanf("%d%d", &n, &m);
    x[1] = 1;
    maxR = 0;
    memset(bestx, 0, sizeof(bestx));
    bestx[1] = 1;
    dfs(2, 1);
    printf("最大连续邮资区间：%d\n", maxR);
    printf("最佳面值设计：");
    for (i = 1; i <= n; i++)
        printf("%d ", bestx[i]);
    printf("\n");
    return 0;
}

五、效果展示

以n=5, m=4，最佳设计面值与最大区间结果为例：

请输入面值种类n, 信封最多贴票数m: 5 4
最大连续邮资区间：70
最佳面值设计：1 3 11 15 32

六、时间复杂度分析

假设有n种票面，回溯法要求枚举所有可能的邮票面值组合，且每组组合用DP方法计算最大区间。

• 搜索树：第1类面值固定为1，第2~n类分别尝试递增赋值，设最大枚举上限T，则组合数约为O(Tn−1)。
• 每次组合Postage区间评估：对每个组合，需要用动态规划求最大连续可达区间，单次DP复杂度约为O(mnS)（S为最大邮资区间，实践中有常数上界）。
• 总体复杂度：为O(Tn−1⋅mnS)，实际运行时n一般不大，否则计算资源将快速耗尽，只能经验剪枝。

七、总结

连续邮资问题是回溯+剪枝+动态规划结合体，适合进阶训练设计高效搜索算法，对算法竞赛与职位笔试很有帮助！