动态规划问题之乘积为正数的最长子字符串问题

hello，everyday，今天，我们继续学习动态规划问题！！准备好了吗？？我们开始了！！！

一.题目描述

我们来稍微解读一下题目，题目中说到：一个数组的子数组是由原数组中零个或者多个连续的数字组成的数组。也就是说，输出的结果可以为0，但是不大可能！！

我们分析一下实例一，数组中没有0，由两个负数，所以负负得正，最大的长度就为整个数组的长度。

接着实例二，数组中有一个0，排除运算，有3个负数，3个负数相乘，结果还为负数，所有只能有2个负数参与运算，还有一个正数，2+1=3，所以最长的长度为3；

相信大家通过对2个例子的分析都知道是什么意思了！！！接下来，我们就用动态规划的方式来解决这道题目！！

二.讲解算法原理

1.状态表示

我们解决这类问题都是依据做题的经验+题目解析。经验就是创建数组，然后进行分析，分析的方向分为两种：1.以某个下标的元素为结尾，然后向前分析，2.以某个下标的元素为开始，然后向后分析。这两种思路可谓是百试不爽，很奏效！！！所以我们沿用一贯的思路，创建数组

f[i]表示：以i位置为结尾的所有子数组中乘积为正数的最长子数组的长度

 有同学可能会有这样的疑问：为什么创建的数组名是f，不是我们经常使用的dp表呢？？这里，我先不告诉大家，卖个关子！！

2.状态转移方程

刚刚，我们凭借这做这类题目的经验，创建了数组，接下来，就是我们深挖题目的时候了。

我向大家抛出这样一个问题：f[i]和f[i-1]之间有什么关系吗？f[i]和f[i+1]之间有什么关系吗？不仅仅在这道题目中要思考这样一个问题，其他的动态规划问题也是如此。

我画一个图：

如图中我所标注的i下标的位置,我们取名题目中的数组为nums，以利于我们分析

1>子数组的长度为1

A.nums[i]>0

此时，符合题目要求的长度为1。

B.nums[i]<0

此时，符合题目要求的长度为0

2>子数组的长度大于1

A.nums[i]>0

身为一个大学生，我们都知道正数乘正数，得到的结果为正数。我们回到此情形中，数组长度大于1，nums[I]>0,所以，要求以下标为i-1元素为结尾的子数组乘积为正数，这不就是f[i-1]嘛，嗦嘎！！！所以f[i]=f[i-1]+1,不单单本题符合f[i]=f[i-1]*K（k需要我们自己去从题目中挖掘）或者f[i]=f[i-1]+k(k需要我们自己从题目中去挖掘)，很多动态规划问题背后都隐藏这个公式。

B.nums[i]<0

这时，我们就需要以下标为i-1元素为结尾的子数组乘积为负数，这时，我们的创建的数组f就无法实现这个功能了，因此，我们就需再创建一个g表！！！

g[i]表示：以i为结尾的所有子数组中乘积为正数的最大值

然后依据nums[i]>0的逻辑，是不是该推导出公式：f[i]=g[i-1]+1?是这样吗？？我们仔细思考一下，错错错！！"why"?因为如果g[i-1]=0,意味着：以下标为i-1的元素结尾的所有子数组中，乘积都是正数，然后代入我们自己推导出来的公式，得到f[i]=1，但我们一想：这种情况，f[i]应该为零，所以错误就产生了，我们可以用三目表达式解决这个问题：

f[i]=g[i-1]==0?0:g[i-1]+1

总结一下：

 

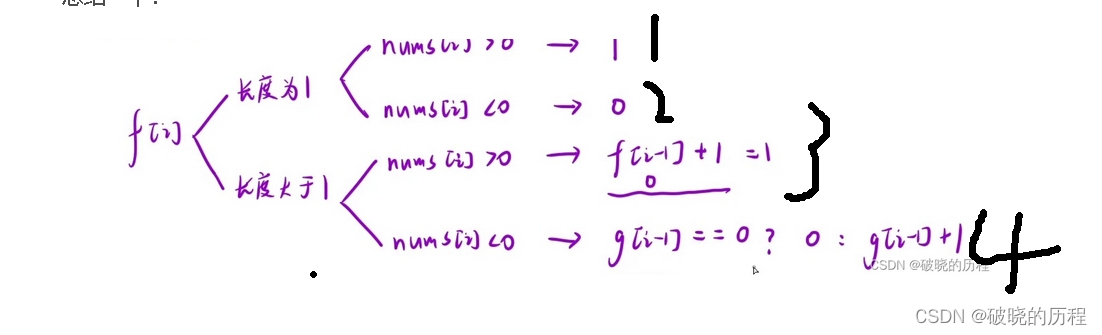
我们发现1,3和2,4可以整合一下：

然后就是g[i]了，g[i]的分析方式和f[i]很像，我就不再详细的说了，把结果给大家，大家自己分析

同样，整合一下：

3.初始化

一提到初始化，我们就需要思考这样两个问题：

1.在什么情况下，会出现越界问题？

2.如何防止越界问题？？

首先我告诉大家：越界问题通常是出现在边界时，对于数组而言，也就是下标等于0时。

对于本题就是如此，当i=0时，i-1=-1会出现越界。

那如何防止越界呢？这里有两种不同的方案：

1.对可能发生越界的位置，手动进行赋值

2.在原来的0下标位置，再添加一个元素，原先的数组整体向后平移一个元素大小的位置，但要注意：

A.新加的位置所填的数据，不能影响到后边的填表

B.要注意因数组大小发生变化而引起的下标变化问题

（技巧：如果状态转移方程中dp[i]和dp[i-1]是dp[i]=dp[i-1]*K的关系，一般新添位置的应该存1；如果状态转移方程中dp[i]和dp[i-1]是dp[i]=dp[i-1]+K的关系，一般新添位置的应该存0）

 这里，我们选择方案二来解决本题：

我们拿g[i]来简单说明， 我们通过观察状态转移方程，不难发现当所填数据等于0时：

 

正好满足我们所想，所以填入0是正确的

4.填表顺序

从左往右，同时填表

5.返回值

返回f表中的最大值

三.代码实现