回溯算法解决组合问题

---

回溯算法

回溯算法是一种搜索方式，本质上其实就是穷举出所有可能，然后筛选出我们想要的答案。

回溯算法的效率并不高，但是能解决一些暴力搜索解决不了的问题，比如组合问题。

组合问题

组合问题：在n个数里面按一定规则找出k个数的集合。

组合与排列的区别：组合是不强调元素顺序的，排列是强调元素顺序。

简单的、数据小的组合问题可以通过暴力解决，比如在10个数中找出2个数的组合，只需要2个for循环嵌套就可以解决。

for(i = 0; i < n; i++)
{
	for(j = i + 1; j < n; j++)
	{
		//i与j排列组合
	}
}

但是如果涉及到更大的数据时，比如在100个数里找出50个数的组合，我们就需要50个for循环嵌套，这样的问题就不能通过暴力去解决。

回溯算法在组合问题上的运用

具体思路如下图：

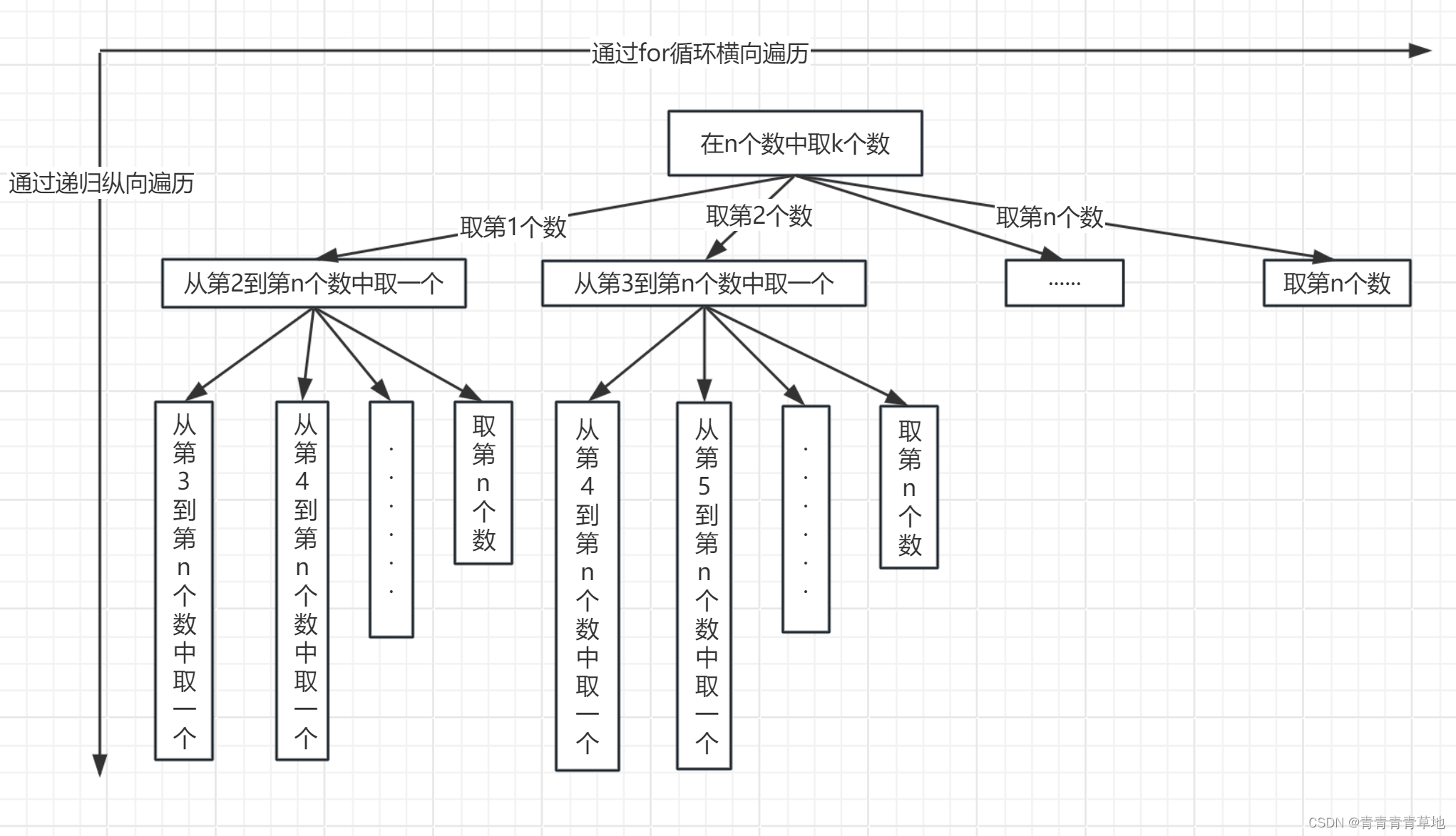
代码模板：

 void dfs(int cur, int n, int k)
 {
    if()//当条件满足判断时，说明我们得到一个符合条件的结果
    {
        //将该结果储存起来
        return;//返回函数上一级去尝试下一种可能
    }
    for(){
		//通过for循环横向遍历需要处理的结点
		dfs(下一个结点)//递归，用同样的方法去处理该节点的下一个结点
		//撤销处理过的结点
	}
 }

例题

Leetcode 77. 组合

给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。

你可以按 任何顺序 返回答案。

示例 1：
输入：n = 4, k = 2
输出：
[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]

示例 2：
输入：n = 1, k = 1
输出：[[1]]

提示：
1 <= n <= 20
1 <= k <= n

/**
 * Return an array of arrays of size *returnSize.
 * The sizes of the arrays are returned as *returnColumnSizes array.
 * Note: Both returned array and *columnSizes array must be malloced, assume caller calls free().
 */
 int *temp; //用来存放某一条组合
 int tempsize;
 int **ret; //用来存放符合条件的结果
 int retsize;
 void dfs(int cur, int n, int k)
 {
    if(tempsize == k)//满足条件当某一条组合中元素的数量达标，将该结果存入ret中
    {
        int *tmp = malloc(sizeof(int) * k);
        for(int i = 0; i < k; i++)
        {
            tmp[i] = temp[i];
        }
        ret[retsize++] = tmp;
        return;//返回上一层函数
    }
    int j;
    for(j = cur; j <=n ;j++) {
        temp[tempsize++] = j;//将一个新的可能放入组合中
        dfs(j + 1, n, k);//递归，完善这个可能
        tempsize--;//回溯，撤销处理过的可能
    }
 }
int** combine(int n, int k, int* returnSize, int** returnColumnSizes) {
    temp = (int*)malloc(sizeof(int) * k);
    ret = (int **)malloc(sizeof(int*) * 20);
    tempsize = 0;
    retsize = 0;
    dfs(1, n, k);
    *returnSize = retsize;
    *returnColumnSizes = malloc(sizeof(int) * retsize);
    for (int i = 0; i < retsize; i++) {
        (*returnColumnSizes)[i] = k;
    }
    return ret;
}

Leetcode 216. 组合总和 III

找出所有相加之和为 n 的 k 个数的组合，且满足下列条件：

• 只使用数字1到9
• 每个数字 最多使用一次
• 返回所有可能的有效组合的列表。该列表不能包含相同的组合两次，组合可以以任何顺序返回。

示例 1:
输入: k = 3, n = 7
输出: [[1,2,4]]
解释:
1 + 2 + 4 = 7
没有其他符合的组合了。

示例 2:
输入: k = 3, n = 9
输出: [[1,2,6], [1,3,5], [2,3,4]]
解释:
1 + 2 + 6 = 9
1 + 3 + 5 = 9
2 + 3 + 4 = 9
没有其他符合的组合了。

示例 3:
输入: k = 4, n = 1
输出: []
解释: 不存在有效的组合。在[1,9]范围内使用4个不同的数字，我们可以得到的最小和是1+2+3+4 = 10，因为10 > 1，没有有效的组合。

提示：
2 <= k <= 9
1 <= n <= 60

/**
 * Return an array of arrays of size *returnSize.
 * The sizes of the arrays are returned as *returnColumnSizes array.
 * Note: Both returned array and *columnSizes array must be malloced, assume caller calls free().
 */
 int **ret;
 int retsize;
 int *temp;
 int tempsize;
 void dfs(int p, int k, int n, int sum)
 {
    if(tempsize == k)
    {
        if(sum == n)
        {
            int *tmp = malloc(sizeof(int) * k);
            for(int i = 0; i < k; i++)
            {
                tmp[i] = temp[i];
            }
            ret[retsize++] = tmp;
        }
        return;
    }
    int j;
    for(j = p; j <=9 ;j++)
    {
        temp[tempsize++] = j;
        sum += j;
        dfs(j + 1, k, n, sum);
        tempsize--;
        sum -= j;
    }
 }
int** combinationSum3(int k, int n, int* returnSize, int** returnColumnSizes) {
    retsize = 0;
    tempsize = 0;
    temp = (int*)malloc(sizeof(int) * k);
    ret = (int **)malloc(sizeof(int*) * 20);
    dfs(1, k, n, 0);
    *returnSize = retsize;
    *returnColumnSizes = (int*)malloc(sizeof(int) * retsize);
    for (int i = 0; i < retsize; i++)
    {
        (*returnColumnSizes)[i] = k;
    }
    return ret;
}

Leetcode 17. 电话号码的字母组合

给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。答案可以按 任意顺序 返回。

给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

示例 1：
输入：digits = “23”
输出：[“ad”,“ae”,“af”,“bd”,“be”,“bf”,“cd”,“ce”,“cf”]

示例 2：
输入：digits = “”
输出：[]

示例 3：
输入：digits = “2”
输出：[“a”,“b”,“c”]

提示：
0 <= digits.length <= 4
digits[i] 是范围 [‘2’, ‘9’] 的一个数字。

/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
 char* temp;
int tempsize;
char** ret;
int retsize;
 char* letterMap[10] = {"", 
        "", 
        "abc", 
        "def", 
        "ghi", 
        "jkl",
        "mno", 
        "pqrs", 
        "tuv", 
        "wxyz", 
};
void dfs(char *digits, int cur)
{
    if(tempsize == strlen(digits))
    {
        char *tmp = (char *)malloc(sizeof(char) * (strlen(digits) + 1));
        int i;
        for(i = 0; i < strlen(digits); i++)
        {
            tmp[i] = temp[i];
        }
        tmp[i] = '\0';
        ret[retsize++] = tmp;
        return;
    }
    int num = digits[cur] - '0';
    char *table = letterMap[num];
    for(int j = 0; j < strlen(table); j++)
    {
        temp[tempsize++] = table[j];
        dfs(digits, cur + 1);
        tempsize--;
    }
}
char** letterCombinations(char* digits, int* returnSize) {
    int n = strlen(digits);
    *returnSize = 0;
    if(n == 0)
    {
        return "";
    }
    ret = malloc(sizeof(int*) * 2000);
    temp = malloc(sizeof(int) * n);
    tempsize = 0;
    retsize = 0;
    dfs(digits, 0);
    *returnSize = retsize;
    return ret;
}