【计算思维课上内容复习】递归

Gusare

已于 2024-05-18 17:57:04 修改

阅读量931

点赞数 22

分类专栏：【复盘】计算思维文章标签：算法 c++

于 2024-05-18 17:50:29 首次发布

本文链接：https://blog.csdn.net/2301_79620132/article/details/138999412

版权

【复盘】计算思维专栏收录该内容

13 篇文章 0 订阅

订阅专栏

理论

递归=“递进”+“回归”

递归：将大问题分解为更小的同质问题

三要素：1.终止条件 2.终止时的处理方法 3.提取重复逻辑（同质）

例1: 斐波那契数列

数学公式：

$F(n)=\begin{cases} & 0 \ (n= 0) \\ & 1 \ (n=1) \\&F(n-1)+F(n-2)\ (n>1)\end{cases}$

（1）原版

long long int Fibonacci(int n)
{
    if(n==0) return 0;
    else if(n==1) return 1;
    else return Fibonacci(n-1)+Fibonacci(n-2);
}

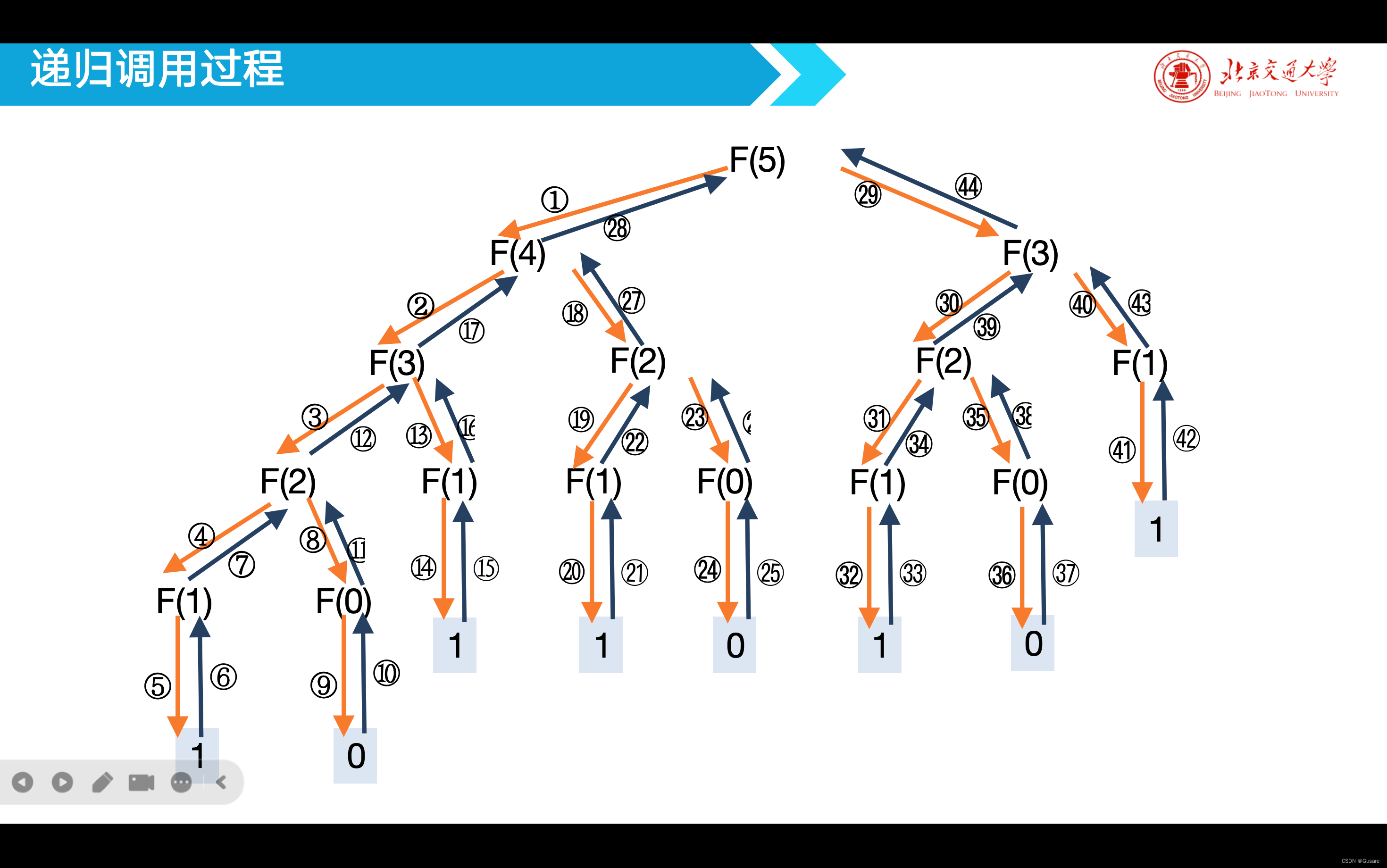
感觉fibonacci的递归过程很像二叉树的前序遍历。f(n)=f(n-1)+f(n-2)的结构就很二叉树！

（2）记忆化递归（空间换时间）

#define MAX 10000
long long int fvs[MAX]={0};
long long int Fibonacci(int n)    //Fibonacci函数：返回第n位的斐波那契数
{
    if(n==0) return 0;
    if(n==1) return 1;
    if(fvs[n]==0) fvs[n]= Fibonacci(n-1)+Fibonacci(n-2);
    return fvs[n];      //如果在之前的递归里已经算过fvs[n]就直接读取数组里存的数
}                       //如果没有则调用Fibonacci递归计算该位的斐波那契数，存入数组

例2: 最大公约数

（1）枚举法

#include<algorithm>
using namespace std;
int Max_Common_Divisor(int a,int b)
{
    for(int i=min(a,b);i>=1;i--)//小技巧：从大到小枚举则符合条件的第一个就是最大的公约数
    {
        if(a%i==0 && b%i==0)
            return i;
    }
}

（2）辗转相除法

$gcd(a,b)(a\geq b)=\begin{cases} & gcd(b,a\%b) \ \ b\neq 0 \\ & a\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ b=0 \end{cases}$

$b\neq 0$ 的情况就相当于是分解成了同质跟小问题，而递归的终点是 $b=0$

（a和b是位置对应关系）（好有意思）

void swap(int &a,int &b)
{
    int tmp;
    tmp=a;
    a=b;
    b=tmp;
}
int gcd(int a,int b)
{
    if(a<b) swap(a,b);
    if(b==0) return a;
    else return gcd(b,a%b);
}

例3: 全排列问题

（1）问题分析

$X$ ：集合，例如{1,2,3,4}

$Perm(X)$ ： $X$ 集合的所有排列情况（集合 $X$ 的全排列）

用递归的思路：X的全排列，等价于集合 $X$ 其中的n个元素分别放在首位，剩下的元素形成一个子集的排列。这样就分解成了求子集的全排列问题。

数学表达式： $Perm(X)=\sum \{r_i\}Perm(X-\{r_i\})$

（2）举例

举个例子：

$X=\{1,2,3,4\}$

求 $X$ 的全排列即：

$Perm(\{1,2,3,4\})=\{1\}Perm(\{2,3,4\})+\{2\}Perm(\{1,3,4\})+\{3\}Perm(\{1,2,4\})+\{4\}Perm(\{1,2,3\})$

（3）代码

#include<iostream>
#include<string>
using namespace std;
void swap(int &a,int &b)
{
    int tmp;
    tmp=a;
    a=b;
    b=tmp;
}
void func(string s,int begin,int end)    //func：打印所有排列情况
{
    if(begin<0||end>=s.length()) {        //防止下标越界
        cout<<"参数传递错误"<<endl;
        return ;
    }
    if(begin>end) {                        //保证begin<=end
        cout<<"起点大于终点，已交换"<<endl;
        swap(begin,end);
    }
    if(begin==end){                        //begin==end排列后与排列前相同
        cout<<s<<endl;
        return ;
    }                              //前三个if提高了程序健壮性，不是全错排的内容
    for(int i=begin;i<=end;i++)    //通过swap函数保证s[begin]是公式中的ri
    {                              //这样全错排的范围就是固定的[begin+1,end]了
        swap(s[begin],s[i]);
        func(s,begin+1,end);
        swap(s[begin],s[i]);
    }
}

这份代码其实是部分排列，想实现全排列即begin=0,end=s.length()-1

例4: 整数划分

（1）问题说明

给两个数n和m，其中n代表集合里元素个数，m代表要分割成非空子集的数目。

函数S(n,m)代表大小为n的集合，分割成m个非空子集的所有情况的数目。

比如 $S(3,2)$ ，即大小为3的集合（不妨理解成 $\{1,2,3\}$ ），要分割成2个非空子集的所有情况数。

即： $\{\{1,2\},\{3\}\}$ ， $\{\{1,3\},\{2\}\}$ ， $\{\{2,3\},\{1\}\}$

所以 $S(3,2)=3$

（2）问题分析

终止情况

（1） $n=0$ 集合为空，分割情况数直接为0

（2） $m=1$ 子集名额只有一个，那子集就是集合本身，分割情况数为1

一般情况

对于 $X$ 中任一元素 $x_i$ ，有两种选择：

（1）单独形成一个子集，即 $\{X-x_i,\{x_i\}\}$

（2）与其他个别元素放在一个子集内，即 $\{\{...x_i...\}...\}$

对于（1）， $X-x_i$ 的分割情况就是 $S(n-1,m-1)$

$n-1$ ： $x_i$ 已经不在讨论范围内

$m-1$ : 刨掉了 $x_i$ 单独使用的一个非空子集名额，剩下了m-1个名额可供其他元素使用

对于（2），相当于在 $S(n-1,m)$ 的情况下 $x_i$ 插空

$m$ ： $x_i$ 是插空进入子集内，所以不占用非空子集的名额，仍为m

$S(n-1,m)$ 本身完全没有考虑 $x_i$ 的放置，作为 $S(n,m)$ 的一个分支情况是不完整的

m个子集可供 $x_i$ 挑选，所以考虑了 $x_i$ 后的 $m \cdot S(n-1,m)$ 才是（2）的完全体

所以，一般递归公式为：

$S(n,m)=m\cdot S(n-1,m)+S(n-1,m-1)$

考虑特殊情况

（1） $n<m$ ：元素比子集名额还少，必然有子集为空集的情况出现， $S(n,m)=0$

（2） $n=m$ ：子集名额和元素数一样，子集非空，则每个子集必然只有一个元素， $S(n,m)=1$

综上

$S(n,m)=\begin{cases} & 0 \ (m= 0\ or\ m>n) \\ & 1 \ (n=m\ or\ m=1) \\&m \cdot S(n-1,m)+S(n-1,m-1)\ (0<m<n)\end{cases}$

（3）代码

这道题难的是数学，公式一旦明确了映射成代码很简单。

int S(int n,int m)
{
    if(n==0||m>n) return 0;
    else if(m==n||m==1) return 1;
    else if(0<m&&m<n) return m*S(n-1,m)+S(n-1,m-1);
    else return -1;
}

例5: 棋盘覆盖问题

ChessBoard(tr+s,tc,tr+s,tc+s-1)：表示用于同质化的蓝色方块视作了特殊方块。位置在左下子棋盘的右上。

其他位置同理。

fill函数（不完全）：

void fill(int tr,int tc,int dr,int dc)
{
    if(tr==dr&&tc==dc)  //特殊方块在左上角
    {
        Chessboard[tr+1][tc+1]=Chessboard[tr+1][tc]=Chessboard[tr][tc+1]=4;
    }
    else if(tr==dr&&tc==dc-1)  //特殊方块在右上角
    {
        Chessboard[tr+1][tc+1]=Chessboard[tr+1][tc]=Chessboard[tr][tc]=3;
    }
    else if(tr==dr-1&&tc==dc)  //特殊方块在左下角
    {
        Chessboard[tr+1][tc+1]=Chessboard[tr][tc+1]=Chessboard[tr][tc]=2;
    }
    else if(tr==dr-1&&tc==dc-1)  //特殊方块在右下角
    {
        Chessboard[tr][tc]=Chessboard[tr+1][tc]=Chessboard[tr][tc+1]=1;
    }
}

有一点很奇怪，递归到size==2的时候，进入fill函数。

fill函数里传进的dr，dc有两种可能：

（1）[dr][dc]就是题目里给的真的特殊方块。赋值为0。

（2）[dr][dc]是我们为了实现同质化而构造的特殊方块。赋的值由size==4时特殊方块到底在哪一象限决定。所以这个是不确定的。

然而（2）中又分出4种情况，分别赋值1，2，3，4。

老师没有给fill函数的具体代码。所以我有点疑惑。关于构造的特殊方块的赋值问题应该怎么解决，我觉得ppt里面没有说明这点。

个人愚见，可能要在size==4的时候单独设置一个状态变量，同时传进fill里面。但这样代码写起来是不是有点冗余？或者fill里面有什么我没想到的神奇方法可以确定传入的“特殊方块”的坐标应该是（1）还是（2），如果是（2）的话应该是赋1，2，3还是4？用什么方法确定呢。