2025 16届蓝桥杯C/C++b组题目及个人题解

置顶不刷题就会爆炸

于 2025-04-14 21:02:11 发布

阅读量1.5k

点赞数 20

分类专栏：竞赛文章标签： c++ 算法数据结构蓝桥杯

本文链接：https://blog.csdn.net/2301_79696736/article/details/147197180

版权

竞赛专栏收录该内容

2 篇文章

订阅专栏

前言

个人感觉填空题还是比前年要难一点，其他的也是符合蓝桥杯特点(暴力)，没啥算法。

话不多说直接开始

A 移动距离

题目

小明初始在二维平面的原点，他想前往坐标 (233,666)。在移动过程中，他只能采用以下两种移动方式，并且这两种移动方式可以交替、不限次数地使用：

水平向右移动，即沿着 x 轴正方向移动一定的距离。
沿着一个圆心在原点 (0,0)、以他当前位置到原点的距离为半径的圆的圆周移动，移动方向不限（即顺时针或逆时针移动不限）。

在这种条件下，他到达目的地最少移动多少单位距离？你只需要输出答案四舍五入到整数的结果。

解

a题也是没啥说的数学题，本人在考的时候还以为是一个特殊角度60°，风风火火算完发现不是然后又不会函数遗憾被斩于马下。

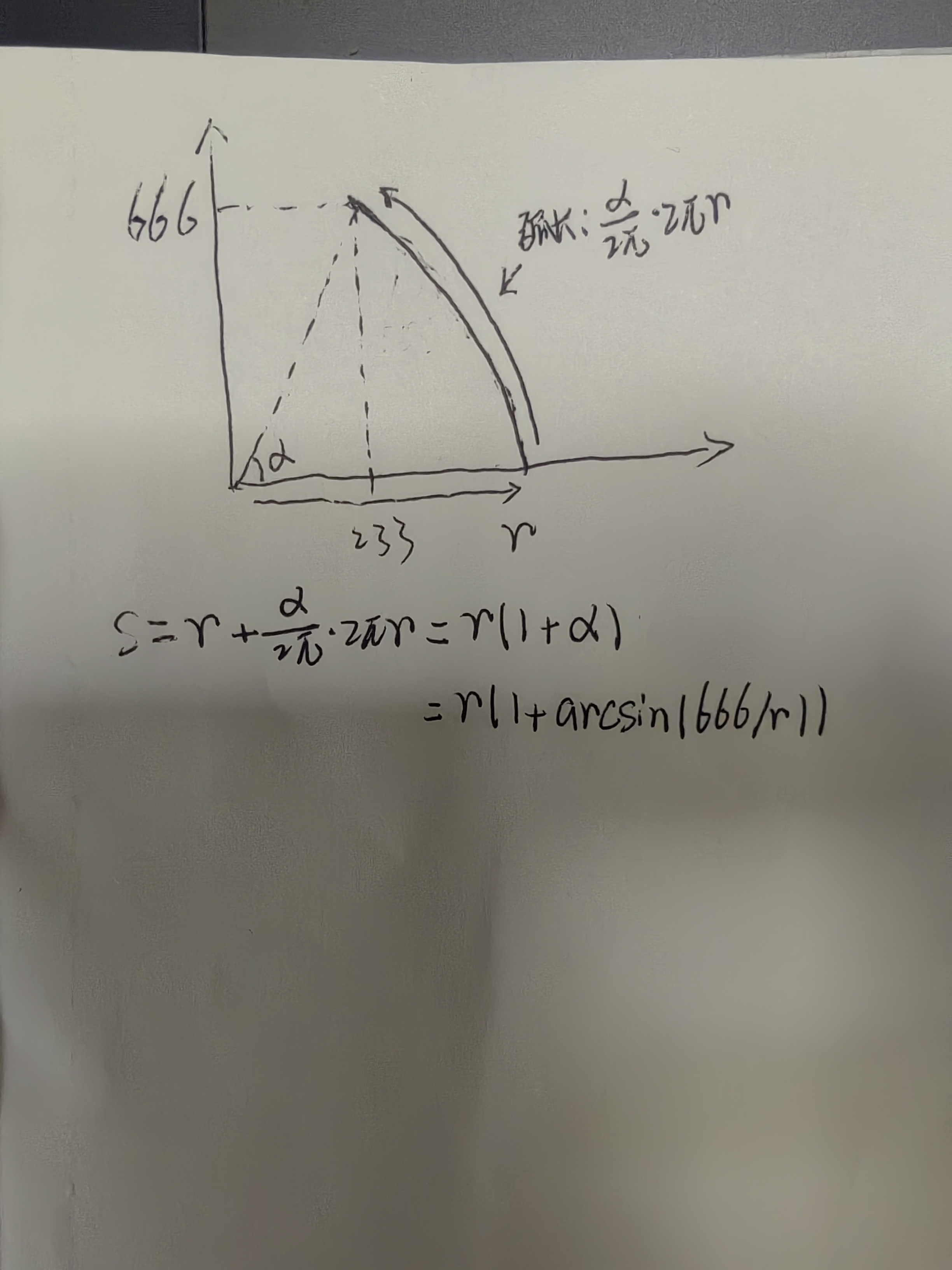
思路大概就是以原点为圆心算出其到坐标 (233,666)的半径，先沿x轴走半径的距离然后沿着圆弧走到坐标即可。

#include <bits/stdc++.h>
int main() {
  double r = sqrt(233 * 233 + 666 * 666);
  int res = r + asin(666.0 / r) * r;
  cout << res;
}

答案似乎是1576

B 客流量上限

题目

一家连锁旅馆在全国拥有 2025 个分店，分别编号为 1 至 2025。随着节日临近，总部决定为每家分店设定每日客流量的上限，分别记作 A1,A2,…,A2025。这些上限并非随意分配，而是需要满足以下约束条件：

A1,A2,…,A2025 必须是 1 至 2025 的一个排列，即每个 Ai 均是 1 至 2025 之间的整数，且所有 Ai 互不相同。
对于任意分店 i 和 j（1≤i,j≤2025，i 可等于 j），它们的客流量上限 Ai 和 Aj 的乘积不得超过 i×j+2025。

这些约束旨在平衡各分店客流压力，确保服务质量和运营稳定性。

现在，请你计算这样的分配方案究竟有多少种。由于答案可能很大，你只需输出其对 109+7 取余后的结果即可。

解

这题就算了没做出来。orz

答案为2的1012次方然后取模

C 可分解的正整数

题目

定义一种特殊的整数序列，这种序列由连续递增的整数组成，并满足以下条件：

序列长度至少为 3。
序列中的数字是连续递增的整数（即相邻元素之差为 1），可以包括正整数、负整数或 0。

例如，[1,2,3]、[4,5,6,7] 和 [−1,0,1] 是符合条件的序列，而 [1,2]（长度不足）和 [1,2,4]（不连续）不符合要求。

现给定一组包含 N 个正整数的数据 A1,A2,…,AN。如果某个 Ai 能够表示为符合上述条件的连续整数序列中所有元素的和，则称 Ai 是可分解的。

请你统计这组数据中可分解的正整数的数量。

输入格式

输入的第一行包含一个正整数 N，表示数据的个数。

第二行包含 N 个正整数 A1,A2,…,AN，表示需要判断是否可分解的正整数序列。

输出格式

输出一个整数，表示给定数据中可分解的正整数的数量。

输入输出样例

输入 #1复制

3
3 6 15

输出 #1复制

说明/提示

样例说明

Ai=3 是可分解的，因为 [0,1,2] 的和为 0+1+2=3。
Ai=6 是可分解的，因为 [1,2,3] 的和为 1+2+3=6。
Ai=15 是可分解的，因为 [4,5,6] 的和为 4+5+6=15。

所以可分解的正整数的数量为 3。

评测用例规模与约定

对于 30% 的评测用例，1≤N≤100，1≤Ai≤100。
对于 100% 的评测用例，1≤N≤105，1≤Ai≤109。

解

分析发现 2可以分解为-1 0 1 2，3可以分解为-2 -1 0 1 2 3以此类推，发现就1不能分解。

那么就简单了，只要发现有1就不要它。

#include<bits/stdc++.h>
using namespace std;
#define endl '\n'
#define ll long long
#define LL long long
#define int long long
#define PII pair<int,int>
#define pii pair<int,PII>
const int mod=1e9+7;


void solve()
{
	int n,ans;
    cin>>n;
    ans=0;
    for(int i=1;i<=n;i++){
        int x;
        cin>>x;
        if(x!=1){
            ans++;
        }
    }
    cout<<ans;
}

signed main()
{
    ios_base::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    int t=1;
    //cin>>t;
    while(t--)
  	{
		solve();
	  }
    
}
//ac orz

D 产值调整

题目

偏远的小镇上，三兄弟共同经营着一家小型矿业公司“兄弟矿业”。公司旗下有三座矿山：金矿、银矿和铜矿，它们的初始产值分别用非负整数 A、B 和 C 表示。这些矿山的产出是小镇经济的核心，支撑着三兄弟和许多矿工家庭的生计。

然而，各矿山的产值波动剧烈，有时金矿收益高而银矿、铜矿低迷，有时则相反。这种不稳定性让公司收入难以预测，也常引发兄弟间的争执。为了稳定经营，三兄弟设计了一个公平的产值调整策略，每年执行一次，每次调整时，将根据当前的产值 A、B、C，计算新产值：

金矿新产值：A′=⌊2B+C⌋；
银矿新产值：B′=⌊2A+C⌋；
铜矿新产值：C′=⌊2A+B⌋；

其中，⌊⌋ 表示向下取整。例如，⌊3.7⌋=3，⌊5.2⌋=5。

计算出 A′、B′、C′ 后，同时更新：A 变为 A′，B 变为 B′，C 变为 C′，作为下一年调整的基础。

三兄弟认为这个方法能平衡产值波动，于是计划连续执行 K 次调整。现在，请你帮他们计算，经过 K 次调整后，金矿、银矿和铜矿的产值分别是多少。

输入格式

输入的第一行包含一个整数 T，表示测试用例的数量。

接下来的 T 行，每行包含四个整数 A,B,C,K，分别表示金矿、银矿和铜矿的初始产值，以及需要执行的调整次数。

输出格式

对于每个测试用例，输出一行，包含三个整数，表示经过 K 次调整后金矿、银矿和铜矿的产值，用空格分隔。

输入输出样例

输入 #1复制

2
10 20 30 1
5 5 5 3

输出 #1复制

25 20 15
5 5 5

说明/提示

评测用例规模与约定

对于 30% 的评测用例，1≤T≤100，1≤A,B,C,K≤105。
对于 100% 的评测用例，1≤T≤105，1≤A,B,C,K≤109。

解

可以发现当a,b,c三矿相等时即可退出，最终尝试次数大概会在 log2max{a,b,c} 左右。

#include<bits/stdc++.h>
using namespace std;
#define endl '\n'
#define ll long long
#define LL long long
#define int long long
#define PII pair<int,int>
#define pii pair<int,PII>
const int mod=1e9+7;


void solve()
{
	int a,b,c,k;
        cin>>a>>b>>c>>k;
        for(int i=1;i<=k;i++){
            int x=a,y=b,z=c;
            a=(y+z)/2;
			b=(x+z)/2;
			c=(x+y)/2;
            if(a==b&&b==c){
                break;
            }
        }
        cout<<a<<" "<<b<<" "<<c<<endl;
}

signed main()
{
    ios_base::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    int t=1;
    cin>>t;
    while(t--)
  	{
		solve();
	  }
    
}
//ac orz

E 画展布置

画展策展人小蓝和助理小桥为即将举办的画展准备了 N 幅画作，其艺术价值分别为 A1,A2,…,AN。他们需要从这 N 幅画中挑选 M 幅，并按照一定顺序布置在展厅的 M 个位置上。如果随意挑选和排列，艺术价值的变化可能会过于突兀，导致观众的观展体验不够流畅。

为了优化布置，他们查阅了《画展布置指南》。指南指出，理想的画展应使观众在欣赏画作时，艺术价值的过渡尽量平缓。指南建议，选择并排列 M 幅画，应使艺术价值的变化程度通过一个数值 L 来衡量，且该值越小越好。数值 L 的定义为：

L=i=1∑M−1∣Bi+12−Bi2∣

其中 Bi 表示展厅第 i 个位置上画作的艺术价值。

现在，他们希望通过精心挑选和排列这 M 幅画作，使 L 达到最小值，以提升画展的整体协调性。请你帮他们计算出这个最小值是多少。

输入格式

输入共两行。

第一行包含两个正整数 N 和 M，分别表示画作的总数和需要挑选的画作数量。

第二行包含 N 个正整数 A1,A2,…,AN，表示每幅画作的艺术价值。

输出格式

输出一个整数，表示 L 的最小值。

输入输出样例

输入 #1复制

4 2
1 5 2 4

输出 #1复制

说明/提示

评测用例规模与约定

对于 40% 的评测用例，2≤M≤N≤103，1≤Ai≤103。
对于 100% 的评测用例，2≤M≤N≤105，1≤Ai≤105。

解

可以发现要使其平方之差最小那么其艺术价值必须接近。那么我们就给其由小到大排序那么两两之间肯定最小，然后我们再算出两两之间的差值前缀和sum[]，以m为范围（sum[i]-sum[i-m]）从m到n选出其中最小(min(ans,sum[i]-sum[i-m]))的即可。

#include<bits/stdc++.h>
using namespace std;
#define endl '\n'
#define ll long long
#define LL long long
#define int long long
#define PII pair<int,int>
#define pii pair<int,PII>
const int mod=1e9+7;
int a[100010],sum[100010];

void solve()
{
	int n, m;
	cin >> n >> m;
	for(int i=1;i<=n;i++)
	 cin >> a[i];
	sort(a+1, a+1+n);
	int ans = 1e12;
	for(int i=2;i<=n;i++)
	{
		sum[i]=sum[i-1]+a[i]*a[i]-a[i-1]*a[i-1]; //前缀和
	}
	for(int i=m;i<=n;i++)
	{
		ans=min(ans,sum[i]-sum[i-m+1]);   //寻找最小的值
	}
	
	cout << ans;
}

signed main()
{
    ios_base::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    int t=1;
    //cin>>t;
    while(t--)
  	{
		solve();
	  }
    
}
//ac orz

F 水质检测

小明需要在一条 2×n 的河床上铺设水质检测器。在他铺设之前，河床上已经存在一些检测器。如果两个检测器上下或者左右相邻，那么这两个检测器就是互相连通的。连通具有传递性，即如果 A 和 B 连通，B 和 C 连通，那么 A 和 C 也连通。现在他需要在河床上增加铺设一些检测器使得所有的检测器都互相连通。他想知道最少需要增加铺设多少个检测器？

输入格式

输入共两行，表示一个 2×n 的河床。

每行一个长度为 n 的字符串，仅包含 # 和 .，其中 # 表示已经存在的检测器，. 表示空白。

输出格式

输出共 1 行，一个整数表示答案。

输入输出样例

输入 #1复制

.##.....#
.#.#.#...

输出 #1复制

说明/提示

样例说明

其中一种方案：

.###....#

.#.######

增加了 5 个检测器。

评测用例规模与约定

对于 100% 的评测用例，保证 n≤1000000。

解

暴力模拟一遍即可，先定义一个结构体A表示河床的一二两层是否存在水质检测器，然后给定双指针l和r，先循环一遍找到l的初值，然后从l+1开始查找，如果遇到该位置i存在水质检测器那么r=i，然后判断r位置河床与l位置河床的一层或者二层是否同时存在水质检测器，如果同时存在那么其间肯定得添加r-l-1个水质检测器，反之则其间肯定得添加r-l个水质检测器。

#include<bits/stdc++.h>
using namespace std;
#define endl '\n'
#define ll long long
#define LL long long
#define int long long
#define PII pair<int,int>
#define pii pair<int,PII>
const int mod=1000000007;
struct A
{
	int s1,s2;    //s1表示一层，s2表示二层，为1代表存在水质检测器，反之则无；
}a[1000010];


void solve()
{
	int len;
  for(int i=1;i<=2;i++)
  {
  	string s;
  	cin>>s;
  	len=s.size();
  	for(int j=0;j<len;j++)
  	{
  		if(i==1&&s[j]=='#')
  		a[j].s1=1;
  		if(i==1&&s[j]=='.')
  		a[j].s1=0;
  		
  		if(i==2&&s[j]=='#')
  		a[j].s2=1;
  		if(i==2&&s[j]=='.')
  		a[j].s2=0;
  		
	}
  }
    int z=0;
  int l=-1,r=-1;
  for(int i=0;i<len;i++)      //查找第一个l与r的位置
  {
  	if(l==-1&&(a[i].s1==1||a[i].s2==1))
  	{
	  l=i;
  		continue;
	  }
  	
  	if(l!=-1&&(a[i].s1==1||a[i].s2==1))
  	{
  		r=i;
  		break;
	  }
  	
  }
  if(l<0||r<0)
  {
  	cout<<0;     //判断特殊条件，不存在两个水质检测器则返回0；
  	return ;
  }
  int ans=0;
  if((a[l].s1==a[r].s1)||(a[l].s2==a[r].s2))
  {
  	ans+=r-l-1;
  }
  else
  {
  	ans+=r-l;
	a[r].s1=1;      //两层都不相等，r位置肯定都会添加水质检测器
 	a[r].s2=1;
  }
l=r;
	for(int i=l+1;i<len;i++)      //暴力即可
	{
		if(a[i].s1==1||a[i].s2==1)
		{
			r=i;
			if(a[l].s1==a[r].s1||(a[l].s2==a[r].s2))
  			{
  			ans+=r-l-1;
  			}
  			else
 			 {
 		 	ans+=r-l;
		  	a[r].s1=1;  
 		 	a[r].s2=1;
			  }
			l=r;
		}
	}
	cout<<ans;
}

signed main()
{
    ios_base::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    int t=1;
    //cin>>t;
    while(t--)
  	{
		solve();
	  }
    
}
//ac orz

G 生产车间

小明正在改造一个生产车间的生产流水线。这个车间共有 n 台设备，构成以 1 为根结点的一棵树，结点 i 有权值 wi。其中叶节点的权值 wi 表示每单位时间将产出 wi 单位的材料并送往父结点，根结点的权值 wi 表示每单位时间内能打包多少单位成品，其他结点的权值 wi 表示每单位时间最多能加工 wi 单位的材料并送往父结点。

由于当前生产线中某些结点存在产能不够的问题导致生产线无法正常运行，即存在某些结点每单位时间收到的材料超过了当前结点的加工能力上限。小明计划删除一些结点使得所有结点都能正常运行。他想知道删除一些结点后根结点每单位时间内最多能打包多少单位的成品？

输入格式

输入共 n+1 行。

第一行为一个正整数 n。

第二行为 n 个由空格分开的正整数 w1,w2,…,wn。

后面 n−1 行，每行两个整数表示树上的一条边连接的两个结点。

输出格式

输出共一行，一个整数代表答案。

输入输出样例

输入 #1复制

9
9 7 3 7 1 6 2 2 7
1 2
1 3
2 4
2 5
2 6
6 7
6 8
6 9

输出 #1复制

说明/提示

样例说明

删掉结点 4、9 后生产线满足条件，根结点 1 每单位时间将打包出 8 单位的成品。

评测用例规模与约定

对于 20% 的评测用例，2≤n≤100。
对于 100% 的评测用例，2≤n≤1000，1≤wi≤1000。

解

这题主播也不会赛时也没做出来orz

H 装修报价

老王计划装修房子，于是联系了一家装修公司。该公司有一套自动报价系统，只需用户提供 N 项装修相关费用 A1,A2,…,AN，系统便会根据这些费用生成最终的报价。

然而，当老王提交数据后，他发现这套系统的运作方式并不透明：系统只会给出一个最终报价，而不会公开任何运算过程或中间步骤。

公司对此解释称，这套系统会依据某种内部算法，在每对相邻数字之间插入 +（加法）、−（减法）或 ⊕（异或）运算符，并按照特定优先级规则计算结果：异或运算优先级最高，其次是加减。但由于保密性，具体的运算符组合以及中间过程都不会对外公开。

为了验证系统报价是否合理，老王决定模拟其运作方式，尝试每种可能的运算符组合，计算出所有可能出现的结果的总和。如果最终报价明显超出这个范围，他就有理由怀疑系统存在异常或误差。只是老王年事已高，手动计算颇为吃力，便向你求助。

现在，请你帮老王算出所有可能的结果的总和。由于该总和可能很大，你只需提供其对 109+7 取余后的结果即可。

输入格式

第一行输入一个整数 N，表示装修相关费用的项数。

第二行输入 N 个非负整数 A1,A2,…,AN，表示各项费用。

输出格式

输出一个整数，表示所有可能的总和对 109+7 取余后的结果。

输入输出样例

输入 #1复制

3
0 2 5

输出 #1复制

说明/提示

对于输入样例中的三个数 A=[0,2,5]，所有可能的运算符组合共有 9 种。计算结果如下：

0⊕2⊕5=7

0⊕2+5=7

0⊕2−5=−3

0+2⊕5=7

0+2+5=7

0+2−5=−3

0−2⊕5=−7

0−2+5=3

0−2−5=−7

所有结果的总和为：

7+7+(−3)+7+7+(−3)+(−7)+3+(−7)=11

11 对 109+7 取余后的值依然为 11，因此，输出结果为 11。

评测用例规模与约定

对于 30% 的评测用例，1≤N≤13，0≤Ai≤103。
对于 60% 的评测用例，1≤N≤103，0≤Ai≤105。
对于 100% 的评测用例，1≤N≤105，0≤Ai≤109。

解

我们造一个样例 1 2 3 4，发现其全部相加除了第一个数或者与第一个数连续异或的数其他的都可以相互正负抵消掉，发现规律由第3个入手，1与2异或不能抵消，其后可连接正负3，不能连接异或3，因为连接异或3的话就不能被抵消，而3后面能连接正负4和异或4，因为其无论连接什么都能被抵消。由此代码就能出来了。

#include<bits/stdc++.h>
using namespace std;
#define endl '\n'
#define ll long long
#define LL long long
#define int long long
#define PII pair<int,int>
#define pii pair<int,PII>
const int mod=1e9+7;

ll fp(ll base, ll power) {
    ll result = 1;
    while (power > 0) {
        if (power & 1) {//此处等价于if(power%2==1)
            result = result * base % mod;
        }
        power >>= 1;//此处等价于power=power/2
        base = (base * base) % mod;
    }
    return result;
}


void solve()
{
	int n;
    cin >> n;
    int S = 0;
    int ans = 0;
    for(int i = 1, x; i <= n; i++) {
        cin >> x;
        S ^= x;
        if(i < n) {
            ans += S * 2 * fp(3ll, n - i - 1) % mod;  //S为异或前缀和，2为其后一位数正负两种选择，3为后面的数正负异或三种选择，n - i - 1为后面能填符号的个数 
        } else {
            ans += S;//特判最后一位数，就是全部数的异或和 
        }
        ans %= mod;   
    }
    cout << ans << endl;
}

signed main()
{
    ios_base::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    int t=1;
    //cin>>t;
    while(t--)
  	{
		solve();
	  }
    
}
//ac orz