2025蓝桥杯Python6

一、排列组合

知识点

排列：从 n 个不同元素中取出 r 个元素，按照一定的顺序排列起来，称为从 n 个元素中取出 r 个元素的一个排列。
组合：从 n 个不同元素中取出 r 个元素，不考虑顺序，称为从 n 个元素中取出 r 个元素的一个组合。
公式：
排列数公式：$$P(n,r)=n!/(n-r)!$$
组合数公式：$$C(n,r)=n!/r!(n-r)!$$

题目

解题思路：

1. 使用回溯算法，通过递归遍历所有可能的排列
2. 维护一个当前路径(path)和已访问标记(visited)
3. 当路径长度等于数组长度时，找到一个排列
4. 每次递归选择一个未访问的数字加入路径
5. 时间复杂度：O(n*n!)
   空间复杂度：O(n)

class Solution:
    def permute(self, nums: List[int]) -> List[List[int]]:
        # 定义回溯函数，用于生成所有排列
        def backtrack(path, visited):
            """
            :param path: 当前已选择的数字路径
            :param visited: 标记数组，记录哪些数字已被使用
            """
            
            # 终止条件：当路径长度等于输入数组长度时，说明找到一个完整排列
            if len(path) == len(nums):
                # 注意要用path的拷贝，因为path会被后续操作修改
                res.append(path[:])  # 将当前排列加入结果集
                return
            
            # 遍历所有数字
            for i in range(len(nums)):
                # 如果当前数字未被使用
                if not visited[i]:
                    # 做选择：标记该数字为已使用，并加入当前路径
                    visited[i] = True
                    path.append(nums[i])
                    
                    # 递归进入下一层决策树
                    backtrack(path, visited)
                    
                    # 撤销选择：回溯，将数字标记为未使用，并从路径中移除
                    path.pop()
                    visited[i] = False
        
        # 初始化结果列表
        res = []
        # 初始化访问标记数组（所有数字初始都未被使用）
        # 调用回溯函数开始生成排列
        backtrack([], [False]*len(nums))
        # 返回所有排列结果
        return res

二、回溯

知识点

回溯算法：一种通过逐步构建解并回溯来求解问题的算法。当发现当前路径不可能是解时，回溯到上一步，尝试其他可能的路径。
应用：回溯算法常用于求解排列组合问题、子集问题、图的路径问题等。

题目

解题思路：

1. 使用回溯算法逐行放置皇后

2. 用三个集合记录已被占用的列、主对角线和副对角线

3. 主对角线特征：行号-列号=常数

4. 副对角线特征：行号+列号=常数

5. 时间复杂度：O(n!)
   空间复杂度：O(n)

class Solution:
    def solveNQueens(self, n: int) -> List[List[str]]:
        """
        解决N皇后问题的主函数
        :param n: 棋盘大小(n×n)和皇后数量
        :return: 所有合法的皇后放置方案
        """
        
        def backtrack(row, cols, diag1, diag2, path):
            """
            回溯函数，递归放置皇后
            :param row: 当前正在处理的行
            :param cols: 已被占用的列集合
            :param diag1: 已被占用的主对角线集合（行-列=常数）
            :param diag2: 已被占用的副对角线集合（行+列=常数）
            :param path: 当前的棋盘状态
            """
            
            # 终止条件：所有行都已处理完毕
            if row == n:
                # 将棋盘转换为要求的字符串格式
                res.append([''.join(row) for row in path])
                return
            
            # 尝试在当前行的每一列放置皇后
            for col in range(n):
                # 检查当前位置是否安全
                if (col not in cols and 
                    (row - col) not in diag1 and 
                    (row + col) not in diag2):
                    
                    # 放置皇后
                    path[row][col] = 'Q'
                    
                    # 递归处理下一行，更新约束条件
                    backtrack(
                        row + 1,                   # 处理下一行
                        cols | {col},              # 新增被占用的列
                        diag1 | {row - col},       # 新增被占用的主对角线
                        diag2 | {row + col},       # 新增被占用的副对角线
                        path                       # 当前棋盘状态
                    )
                    
                    # 回溯：移除皇后，尝试其他位置
                    path[row][col] = '.'
        
        # 初始化结果列表
        res = []
        # 初始化棋盘（全部填充为'.'）
        # 开始回溯，从第0行开始，初始所有列和对角线都未被占用
        backtrack(0, set(), set(), set(), [['.'] * n for _ in range(n)])
        return res

解题思路：

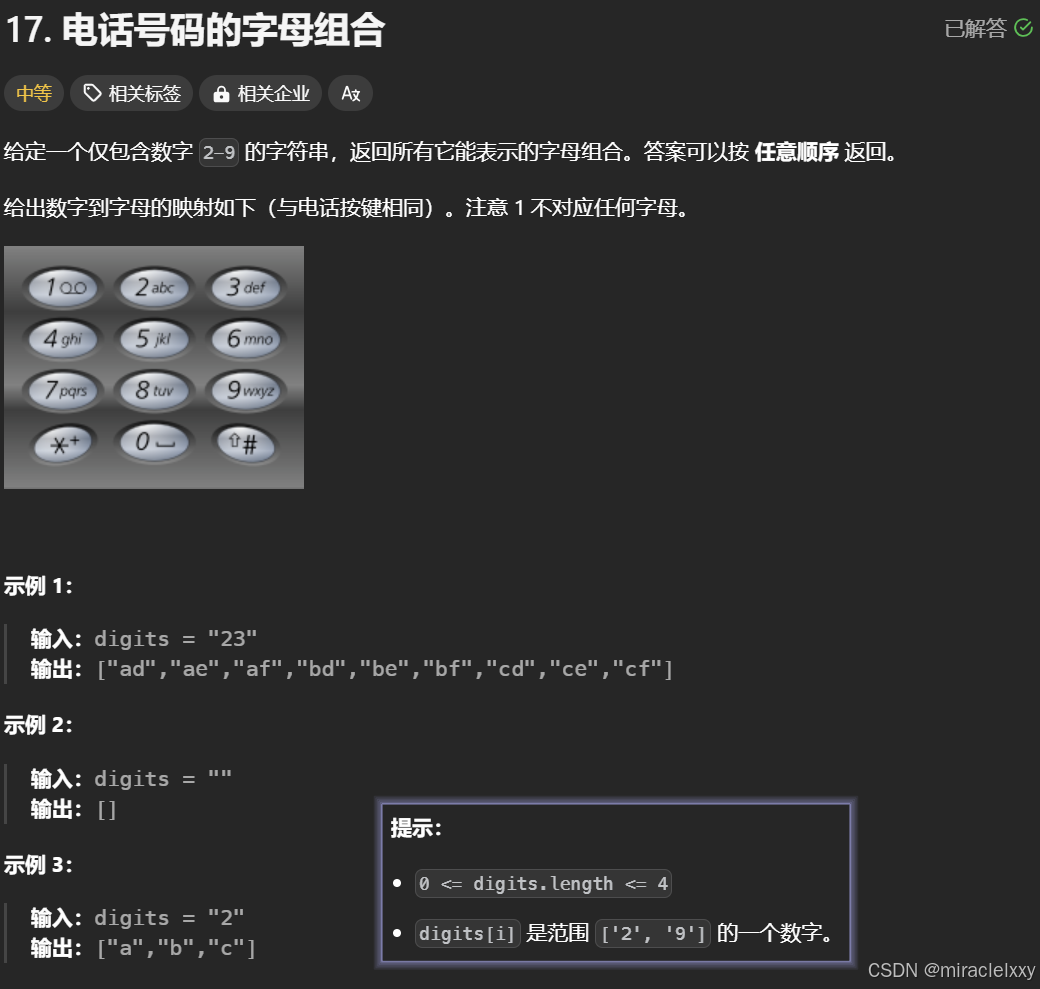
1. 建立数字到字母的映射表

2. 使用回溯算法构建所有可能的组合

3. 每次递归处理一个数字对应的所有字母

4. 时间复杂度：O(3^N × 4^M) 其中N是3字母数字个数，M是4字母数字个数
   空间复杂度：O(3^N × 4^M)

class Solution:
    def letterCombinations(self, digits: str) -> List[str]:
        """
        电话号码字母组合问题：给定数字字符串，返回所有可能的字母组合
        
        参数:
            digits: 数字字符串，例如"23"
            
        返回:
            所有可能的字母组合列表，例如["ad","ae","af","bd","be","bf","cd","ce","cf"]
        """
        
        # 处理空输入的特殊情况
        if not digits:
            return []
        
        # 数字到字母的映射字典
        digit_map = {
            '2': 'abc',
            '3': 'def',
            '4': 'ghi',
            '5': 'jkl',
            '6': 'mno',
            '7': 'pqrs',  # 7和9对应4个字母
            '8': 'tuv',
            '9': 'wxyz'
        }
        
        def backtrack(index, path):
            """
            回溯函数，递归生成所有组合
            
            参数:
                index: 当前处理的数字索引
                path: 当前已生成的字母路径
            """
            # 终止条件：已处理完所有数字
            if index == len(digits):
                res.append(''.join(path))  # 将字符列表转为字符串
                return
                
            # 获取当前数字对应的字母集合
            current_digit = digits[index]
            letters = digit_map[current_digit]
            
            # 遍历当前数字对应的所有字母
            for letter in letters:
                path.append(letter)  # 选择当前字母
                backtrack(index + 1, path)  # 递归处理下一个数字
                path.pop()  # 撤销选择，回溯
        
        # 初始化结果列表
        res = []
        # 从第0个数字开始回溯，初始路径为空
        backtrack(0, [])
        return res

三、求幂

知识点

求幂：计算 aⁿ 的值，其中 a 是底数，n 是指数。
快速幂：一种高效的求幂算法，利用二进制和分治思想，将时间复杂度从 O(n) 降低到 O(logn)。

题目

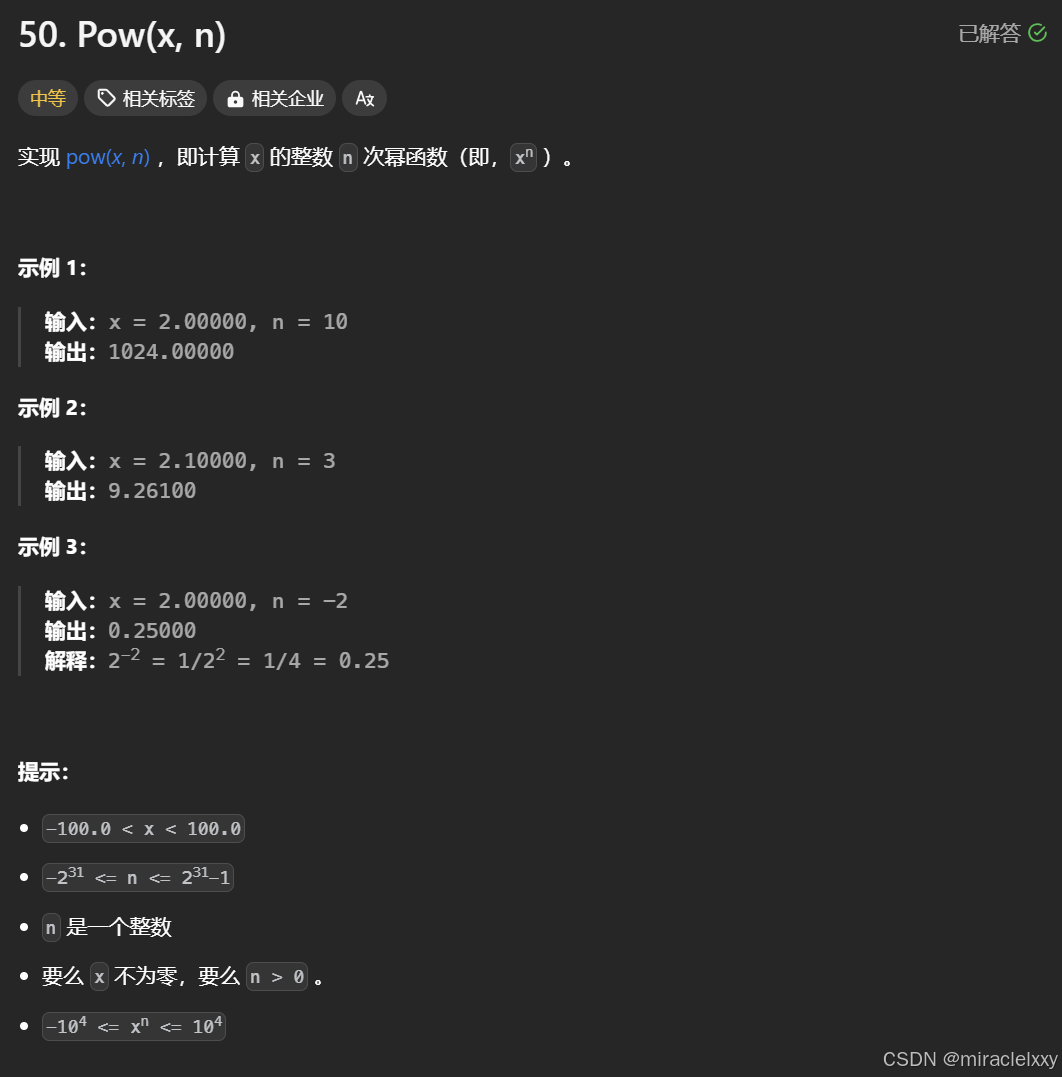
解题思路：

1. 使用快速幂算法，分治思想

2. 将指数n分解为二进制形式

3. 通过不断平方和乘积来减少计算次数

4. 处理负指数情况

5. 时间复杂度：O(logn)
   空间复杂度：O(logn) 递归栈空间

class Solution:
    def myPow(self, x: float, n: int) -> float:
        """
        计算x的n次幂（快速幂算法实现）
        
        参数:
            x: 底数
            n: 指数
            
        返回:
            x的n次幂结果
        """
        
        def fastPow(x, n):
            """
            快速幂递归辅助函数
            
            参数:
                x: 底数
                n: 当前指数
                
            返回:
                当前递归层的计算结果
            """
            # 递归基：任何数的0次方都是1
            if n == 0:
                return 1.0
                
            # 分治：计算x的n//2次方
            half = fastPow(x, n // 2)
            
            # 根据n的奇偶性返回不同结果
            if n % 2 == 0:
                # 如果n是偶数，x^n = (x^(n/2))^2
                return half * half
            else:
                # 如果n是奇数，x^n = (x^(n//2))^2 * x
                return half * half * x
        
        # 处理负指数情况
        if n < 0:
            x = 1 / x  # 取倒数
            n = -n     # 将指数转为正数
            
        # 调用快速幂函数计算结果
        return fastPow(x, n)

四、求素数

知识点

素数定义：素数是一个大于1的自然数，除了1和它本身外，不能被其他自然数整除。
埃拉托斯特尼筛法（Sieve of Eratosthenes）：一种高效的求素数算法，通过逐步标记合数来筛选素数。该算法的基本思想是从小到大遍历每个数，如果当前数是素数，则将其所有的倍数标记为非素数。这样，剩下的未被标记的数就是素数。

题目

解题思路

1. 初始化一个布尔数组 is_prime，长度为 n，初始时所有元素设为 True。is_prime[i] 表示数字 i 是否是质数。

2. 处理特殊情况：0 和 1 不是质数，直接标记为 False。

3. 遍历从 2 开始到 sqrt(n) 的所有数：

4. 如果当前数 i 是质数（即 is_prime[i] 为 True），则将其所有倍数（从 i*i 开始，每次增加 i）标记为非质数。

5. 统计质数的数量：遍历 is_prime 数组，统计值为 True 的个数。

class Solution:
    def countPrimes(self, n: int) -> int:
        """
        计算小于n的质数的数量
        
        参数:
            n: 一个非负整数
            
        返回:
            小于n的质数的数量
        """
        
        # 处理特殊情况：n小于等于2时没有质数
        if n <= 2:
            return 0
        
        # 初始化一个标记数组，表示每个数是否是质数
        # 初始假设所有数都是质数（True表示是质数）
        is_prime = [True] * n
        
        # 0和1不是质数，直接标记为False
        is_prime[0] = is_prime[1] = False
        
        # 埃拉托斯特尼筛法核心部分
        # 只需要检查到sqrt(n)即可，因为更大的数的倍数已经被更小的质数标记过了
        for i in range(2, int(n ** 0.5) + 1):
            # 如果i是质数
            if is_prime[i]:
                # 将i的所有倍数标记为非质数
                # 从i*i开始，因为更小的倍数已经被更小的质数标记过了
                for multiple in range(i * i, n, i):
                    is_prime[multiple] = False
        
        # 统计is_prime数组中True的个数，即为质数的数量
        return sum(is_prime)

五、求约数

知识点

约数定义：如果整数 a 能被整数 b 整除，那么 b 就是 a 的约数。
求约数方法：遍历从1 到 根号n 的所有整数，如果 i 是 n 的约数，那么 n/i 也是 n 的约数。
欧几里得算法：一种求两个整数最大公约数（GCD）的算法，基于原理gcd(a,b)=gcd(b,a % b)。

欧几里得算法详解

欧几里得算法（又称辗转相除法）是计算两个正整数最大公约数（GCD）的高效方法，由古希腊数学家欧几里得在其著作《几何原本》中首次描述。

核心思想

基于一个关键数学原理：
两个数的最大公约数等于其中较小的数和两数相除余数的最大公约数

用公式表示为：
gcd(a, b) = gcd(b, a % b)
直到 b = 0 时，a 就是最终的GCD

计算过程示例

以计算 gcd(48, 18) 为例：

1. 48 ÷ 18 = 2 余 12 → gcd(48,18) = gcd(18,12)
2. 18 ÷ 12 = 1 余 6 → gcd(18,12) = gcd(12,6)
3. 12 ÷ 6 = 2 余 0 → gcd(12,6) = gcd(6,0)
4. 当第二个数为0时，第一个数6就是结果

算法实现

Python中有三种实现方式：

1. 循环实现

def gcd(a, b):
    while b:
        a, b = b, a % b
    return a

2. 递归实现

def gcd(a, b):
    return a if b == 0 else gcd(b, a % b)

3. math模块直接调用

import math
math.gcd(a, b)  # Python 3.5+ 支持

关键特性

• 时间复杂度：O(log(min(a,b)))
  每次迭代数值至少减半
• 空间复杂度：
  • 迭代版：O(1)
  • 递归版：O(log n)（调用栈深度）
• 处理负数：算法会自动取绝对值计算
• 边界情况：
  • gcd(a,0) = |a|
  • gcd(0,0) = 0（数学定义）

实际应用

1. 分数化简：16/24 = (16÷8)/(24÷8) = 2/3
2. 密码学：RSA算法的基础运算
3. 图形学：计算最简屏幕比例
4. 本题解法：找数组极值的GCD

数学证明

设 a = b*q + r（q是商，r是余数）
若有数 d 能整除 a 和 b，则必有 d 能整除 r
因此 gcd(a,b) = gcd(b,r)，直到 r=0 时 b 即为GCD

题目

import math

class Solution:
    def findGCD(self, nums: List[int]) -> int:
        min_num = min(nums)
        max_num = max(nums)
        return math.gcd(min_num, max_num)

扩展欧几里得算法详解

扩展欧几里得算法是欧几里得算法的扩展，不仅能计算最大公约数（GCD），还能找到满足贝祖等式（Bézout’s identity）的整数系数x和y，即：

对于任意整数a和b，存在整数x和y，使得：
ax + by = gcd(a, b)

算法原理

在普通欧几里得算法的每一步中，同时计算系数x和y：

1. 基础情况：当b = 0时，gcd(a,0) = a，此时x = 1，y = 0
2. 递归关系：
   已知gcd(b, a % b) = bx' + (a % b)y'
   因为a % b = a - ⌊a/b⌋ * b
   所以ax + by = bx' + (a - ⌊a/b⌋ * b)y'
   整理得：x = y'，y = x' - ⌊a/b⌋ * y'

Python实现

def extended_gcd(a, b):
    if b == 0:
        return a, 1, 0
    else:
        gcd, x1, y1 = extended_gcd(b, a % b)
        x = y1
        y = x1 - (a // b) * y1
        return gcd, x, y

示例计算

求gcd(99, 78)和对应的x,y：

1. gcd(99, 78) → x = -11, y = 14
   验证：99*(-11) + 78*14 = -1089 + 1092 = 3
   确实gcd(99,78)=3

2. gcd(240, 46) → x = -9, y = 47
   验证：240*(-9) + 46*47 = -2160 + 2162 = 2

关键应用

1. 模反元素计算（用于RSA加密）
   当gcd(a,m)=1时，ax ≡ 1 (mod m)的解x就是a的模反元素

2. 线性同余方程求解
   方程ax ≡ b (mod m)有解当且仅当gcd(a,m)能整除b

3. 中国剩余定理的实现基础

特性分析

• 系数大小：
  |x| < |b/gcd| 和 |y| < |a/gcd|
• 多解性：
  若(x0,y0)是解，则所有解为：
  x = x0 + k*(b/gcd)
y = y0 - k*(a/gcd)
  其中k为任意整数

优化实现（非递归版）

def extended_gcd_iter(a, b):
    x0, x1 = 1, 0
    y0, y1 = 0, 1
    while b:
        q = a // b
        a, b = b, a % b
        x0, x1 = x1, x0 - q * x1
        y0, y1 = y1, y0 - q * y1
    return a, x0, y0

实际应用案例

求17在模43下的乘法逆元：

gcd, x, y = extended_gcd(17, 43)
if gcd == 1:
    inverse = x % 43  # 结果为38
# 验证：17*38 = 646 ≡ 1 mod 43

六、日期处理

知识点

1. 日期格式转换

   • 常见的日期格式包括 YYYY-MM-DD、MM/DD/YYYY 和 DD-MM-YYYY。
   • Python 中的 datetime 模块提供了方便的日期格式转换功能。

   from datetime import datetime
   
   # 将字符串转换为 datetime 对象
   date_str = "2023-04-01"
   date_obj = datetime.strptime(date_str, "%Y-%m-%d")
   
   # 将 datetime 对象转换为字符串
   date_str = date_obj.strftime("%m/%d/%Y")
   

2. 日期加减

   • 在 Python 中，可以使用 datetime.timedelta 对象来计算日期加减。

   from datetime import datetime, timedelta
   
   # 创建一个 datetime 对象
   date_obj = datetime(2023, 4, 1)
   
   # 加 5 天
   date_obj_plus = date_obj + timedelta(days=5)
   
   # 减去 2 小时
   date_obj_minus = date_obj - timedelta(hours=2)
   

3. 日期间隔计算

   • 可以使用 datetime 模块中的 relativedelta 类来计算日期间隔。

   from datetime import relativedelta
   
   # 创建两个 datetime 对象
   start_date = datetime(2023, 1, 1)
   end_date = datetime(2023, 3, 1)
   
   # 计算日期间隔
   interval = relativedelta(end_date, start_date)
   
   print(f"Years: {interval.years}, Months: {interval.months}, Days: {interval.days}")
   

4. 星期计算

   • 计算星期可以使用多种方法，包括蔡勒公式（Zeller’s Congruence）和更通用的计算公式。

   def zeller_congruence(day, month, year):
       if month < 3:
           month += 12
           year -= 1
       q = day
       m = month
       k = year % 100
       j = year // 100
       h = (q + (13 * (m + 1)) // 5 + k + k // 4 + j // 4 + 5 * j) % 7
       return ["Saturday", "Sunday", "Monday", "Tuesday", "Wednesday", "Thursday", "Friday"][h]
   
   # 计算 2023 年 4 月 1 日是星期几
   day, month, year = 1, 4, 2023
   print(zeller_congruence(day, month, year))
   

5. 闰年判断

   • 判断闰年的方法：如果年份能被 4 整除且不能被 100 整除，或者能被 400 整除，则是闰年。

   def isLeapYear(year):
       return (year % 4 == 0 and year % 100 != 0) or year % 400 == 0
   
   print(isLeapYear(2024))  # 输出：True
   

6. 日期计数惯例

   • 常见的日期计数惯例包括实际日计数法、30/360 法和实际/实际法。

   from datetime import datetime
   
   # 定义两个日期
   date1 = datetime(2023, 1, 15)
   date2 = datetime(2023, 2, 15)
   
   # 计算天数差
   delta = date2 - date1
   print(f"两个日期之间相隔的天数：{delta.days}")
   

题目

1. 一周中的第几天

class Solution:
    def dayOfTheWeek(self, day: int, month: int, year: int) -> str:
        """
        使用Zeller's Congruence算法计算给定日期是星期几
        
        参数:
            day: 日 (1-31)
            month: 月 (1-12)
            year: 年 (1971-2100)
            
        返回:
            星期几的字符串 ("Sunday", "Monday", ..., "Saturday")
        """
        
        # 处理1月和2月的情况（Zeller算法要求将1、2月视为上一年的13、14月）
        if month < 3:
            month += 12  # 1月变为13月，2月变为14月
            year -= 1   # 年份减1
        
        # Zeller's Congruence核心计算公式
        # 公式说明：
        # h = (day + 13*(month+1)//5 + year + year//4 - year//100 + year//400) % 7
        # 其中所有除法都是整数除法（地板除）
        h = (day + 13 * (month + 1) // 5 + year + year // 4 - year // 100 + year // 400) % 7
        
        # 将计算结果映射到星期几
        # h的取值范围是0-6，分别对应：
        # 0=星期六, 1=星期日, 2=星期一, 3=星期二, 
        # 4=星期三, 5=星期四, 6=星期五
        days = ["Saturday", "Sunday", "Monday", "Tuesday", 
                "Wednesday", "Thursday", "Friday"]
        
        return days[h]

Zeller’s Congruence（泽勒一致性）算法

Zeller’s Congruence 是由德国数学家克里斯汀·泽勒（Christian Zeller）提出的一种算法，用于计算任何给定日期是星期几。该算法适用于格里高利历（公历）和儒略历。

算法公式

对于格里高利历，公式如下：

其中：

• ( h ) 是星期几（0 = 星期六，1 = 星期日，2 = 星期一，…，6 = 星期五）。
• ( q ) 是一个月中的某一天。
• ( m ) 是月份（3 = 三月，4 = 四月，…，14 = 二月；一月和二月分别视为上一年的13月和14月）。
  

代码实现

def zellers_congruence(day, month, year):
    if month < 3:
        month += 12
        year -= 1

    K = year % 100
    J = year // 100

    h = (day + (13 * (month + 1)) // 5 + K + K // 4 + J // 4 + 5 * J) % 7

    days_of_week = ["Saturday", "Sunday", "Monday", "Tuesday", "Wednesday", "Thursday", "Friday"]

    return days_of_week[h]

# 示例
day = 25
month = 7
year = 2023
day_of_week = zellers_congruence(day, month, year)
print(f"The day of the week for {day}-{month}-{year} is {day_of_week}.")

输出示例

对于日期 2023 年 7 月 25 日，输出结果为：

The day of the week for 25-7-2023 is Sunday.

注意事项

• 一月和二月在公式中被视为上一年的第 13 个月和第 14 个月。
• 该算法适用于格里高利历和儒略历，但公式略有不同。

儒略历公式如下：

代码实现

def zellers_congruence_julian(day, month, year):
    if month < 3:
        month += 12
        year -= 1

    K = year % 100
    J = year // 100

    h = (day + (13 * (month + 1)) // 5 + K + K // 4 + 5 * J) % 7

    days_of_week = ["Saturday", "Sunday", "Monday", "Tuesday", "Wednesday", "Thursday", "Friday"]

    return days_of_week[h]

# 示例
day = 1
month = 1
year = 2023
day_of_week = zellers_congruence_julian(day, month, year)
print(f"The day of the week for {day}-{month}-{year} in the Julian calendar is {day_of_week}.")

2. 日期之间隔几天

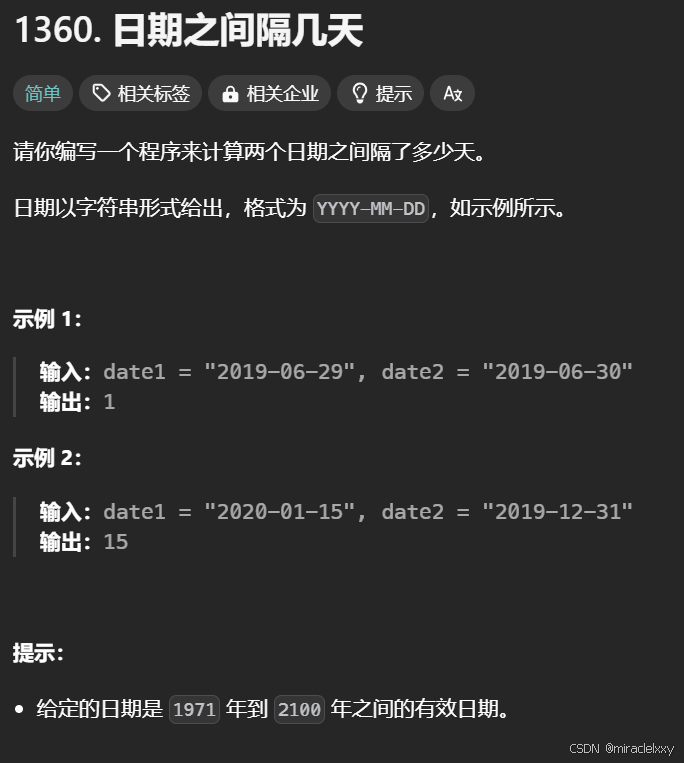
要计算两个日期之间的天数差，可以按照以下步骤进行：

1. 解析日期字符串：将输入的日期字符串分解为年、月、日三个整数。

2. 转换为天数：将每个日期转换为从某个固定日期（如1970-01-01）开始的天数。

3. 计算年份贡献的天数，包括所有整年的天数和闰年的额外天数。

4. 计算月份贡献的天数，注意不同月份的天数不同，特别是闰年2月有29天。

5. 加上当月的天数。

6. 计算差值：将两个日期对应的天数相减，取绝对值即得到它们之间的天数差。

import datetime

class Solution:
    def daysBetweenDates(self, date1: str, date2: str) -> int:
        # 将日期字符串转换为datetime.date对象
        d1 = datetime.date.fromisoformat(date1)
        d2 = datetime.date.fromisoformat(date2)
        # 计算两个日期的差值，并返回绝对天数
        return abs((d2 - d1).days)

3. 计算两个日期之间的工作日天数

from datetime import datetime, timedelta

def workdays(start: str, end: str) -> int:
    start_dt = datetime.strptime(start, "%Y-%m-%d")
    end_dt = datetime.strptime(end, "%Y-%m-%d")

    if start_dt > end_dt:
        raise ValueError("开始日期不能晚于结束日期")

    delta = (end_dt - start_dt).days + 1
    weekends = 0

    for day in range(delta):
        current = start_dt + timedelta(days=day)
        if current.weekday() >= 5:  # 5=周六,6=周日
            weekends += 1

    return delta - weekends

print(workdays("2023-08-01", "2023-08-31"))  # 输出 23

4. 生成指定月份的所有周五日期

import calendar
from datetime import date

def get_fridays(year: int, month: int):
    cal = calendar.monthcalendar(year, month)
    fridays = []
    for week in cal:
        if week[4] != 0:  # 第 5 列是周五
            fridays.append(date(year, month, week[4]).strftime("%Y-%m-%d"))
    return fridays

print(get_fridays(2023, 8))
# ['2023-08-04', '2023-08-11', '2023-08-18', '2023-08-25']

5. 处理夏令时转换边界问题

def test_dst_transition():
    tz = pytz.timezone('America/New_York')
    dt = datetime(2023, 3, 12, 1, 30)  # 夏令时开始时间
    try:
        print(tz.localize(dt, is_dst=None))
    except pytz.AmbiguousTimeError:
        print("检测到存在歧义时间")
    except pytz.NonExistentTimeError:
        print("检测到不存在的时间")

test_dst_transition()  # 输出不存在的时间异常