本文概述了图论中的几个关键定理，如顶点度的性质、奇度顶点、生成子图与子图的区别、图同构、完全图与正则图的概念，以及通路、连通性和连通分支的定义。讨论了度量连通性的方法，包括点割集和边割集，并介绍了k连通图的概念及其连通度特性。
定理1 顶点度之和恰等于边数的两倍
定理2：任意奇度顶点数为偶
证明：巧妙的去一边变换
定理3：关于顶点最大度
子图和生成子图的区别：
生成子图必须V=V’ 顶点必须和母图一致
子图不要求V=V'
图同构
一些特殊的图类型
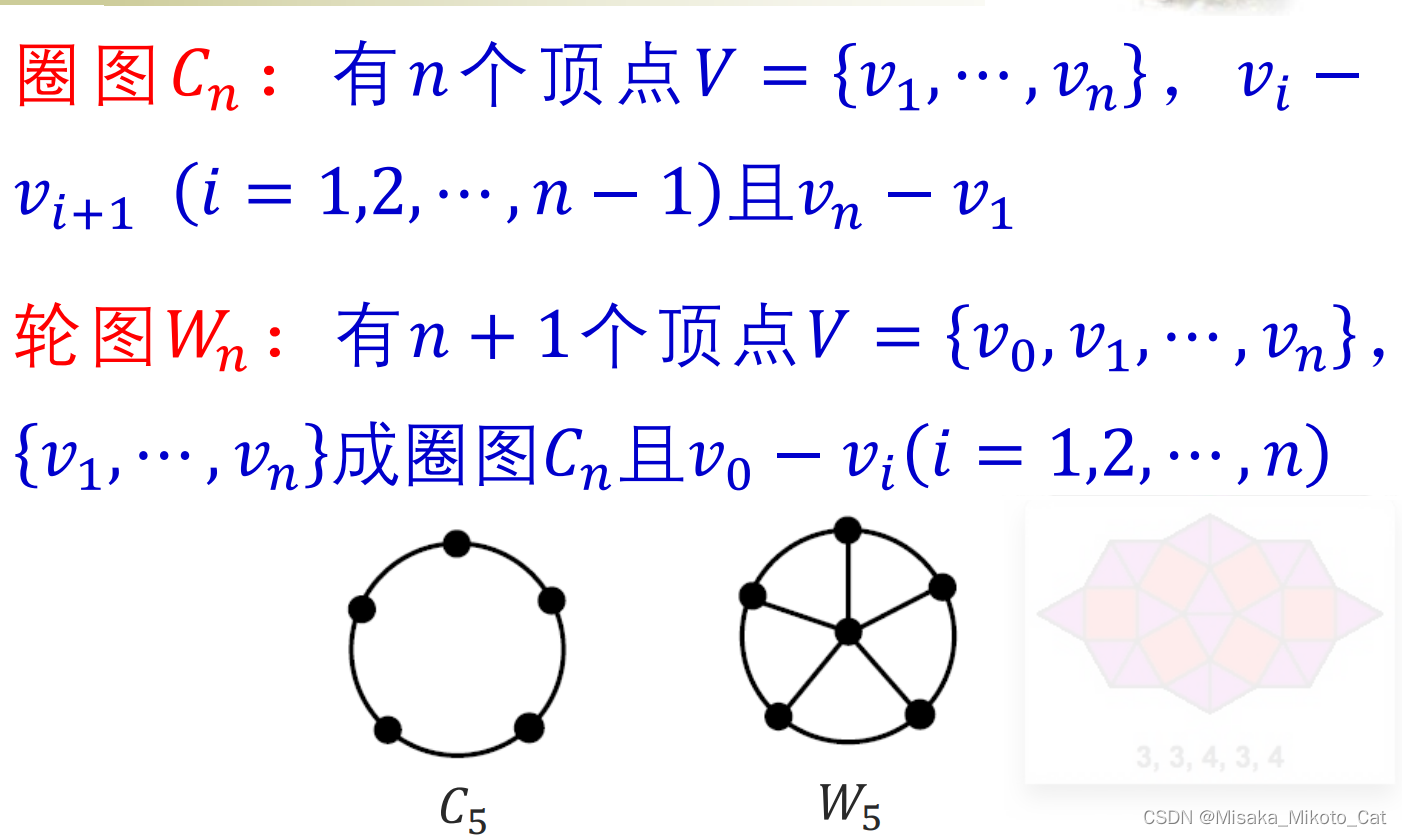
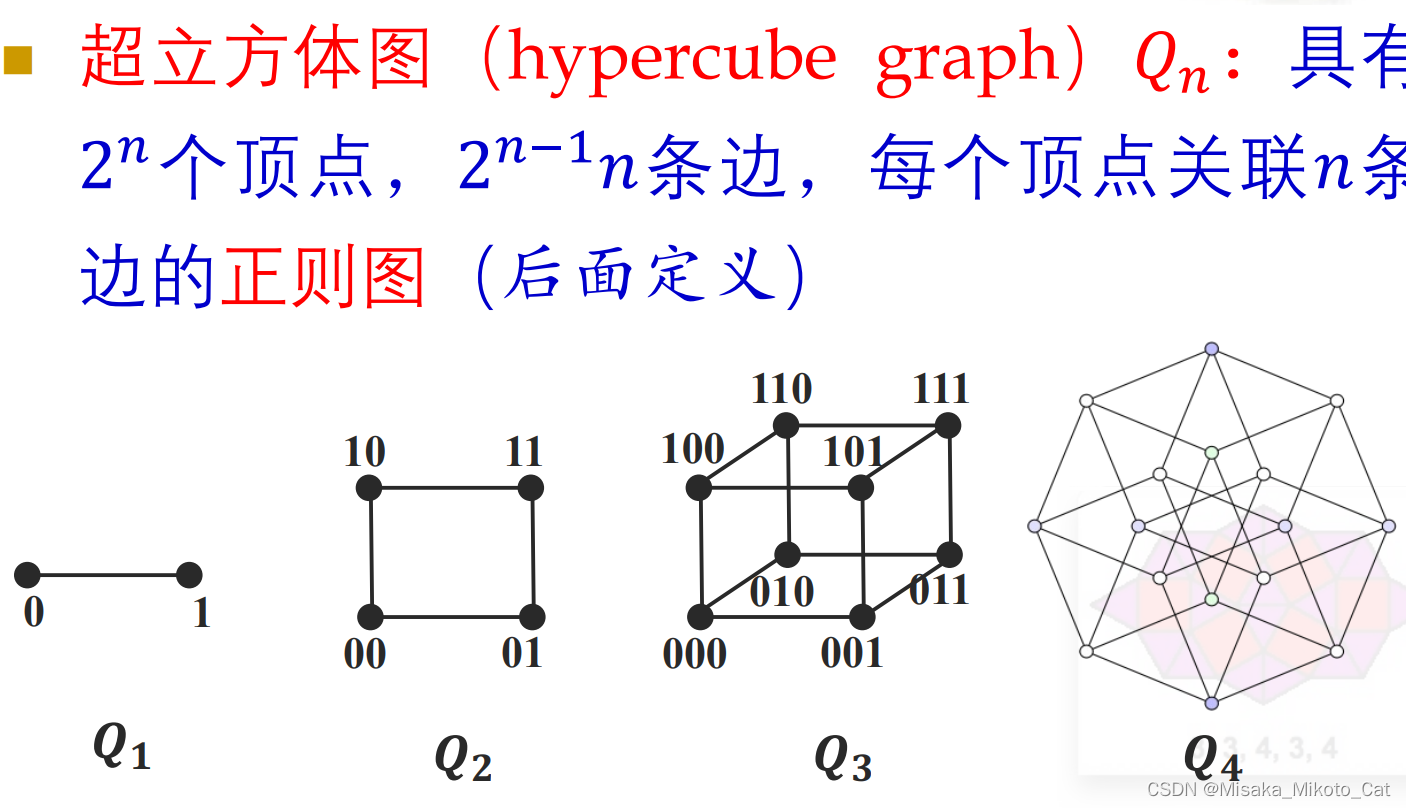
完全图
完全图要求每个顶点都是最大度
故易得对于每个正整数n，完全图都唯一
正则图是完全图的退化版本，每个顶点的个数都是k个
正则图的边数容易计算
二部图可以用边把对应的端点分为两个部分，即是一种划分点集的图。
图的运算
注意：每去掉一个点，相当于去掉与这个点相关联的所有边
通路
简单通路，初级通路区别
简单通路不能包含重复的边，但可以有重复的点
初级通路不能含有重复的边或者重复的点
易有通路存在性定理
将连通定义为之间存在通路
可以得出连通性是一个等价关系
故可以划分出一个等价类
划分出的部分称为连通分支
定理：如果一个图不连通，则其补图连通。、
那么如何度量连通性，即如何描述连通的牢固程度呢？
下面定义点割集和边割集
割集用于描述去除一些元素导致连通分支数增加的元素集合‘
有以下命题
点连通度可以用于描述图的连通程度强与弱
k连通图指删除少于k个顶点无法使其不连通的图。
下面是一些特殊图的连通性
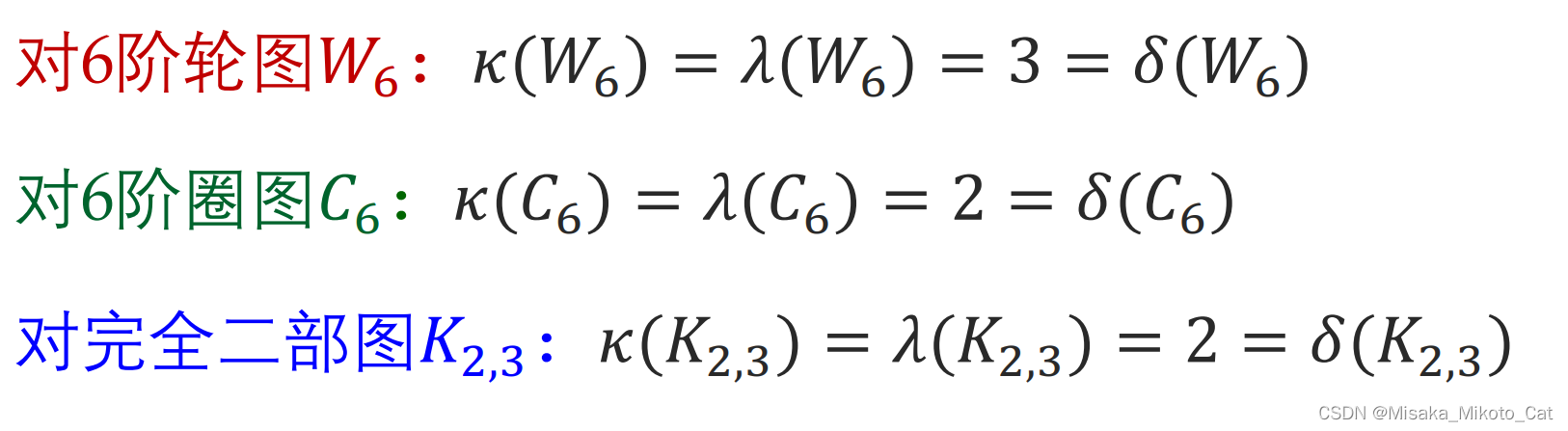
对于连通度有如下结论
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
