【leetcode C++】动态规划

 

13. LCR 091. 粉刷房子

题目：

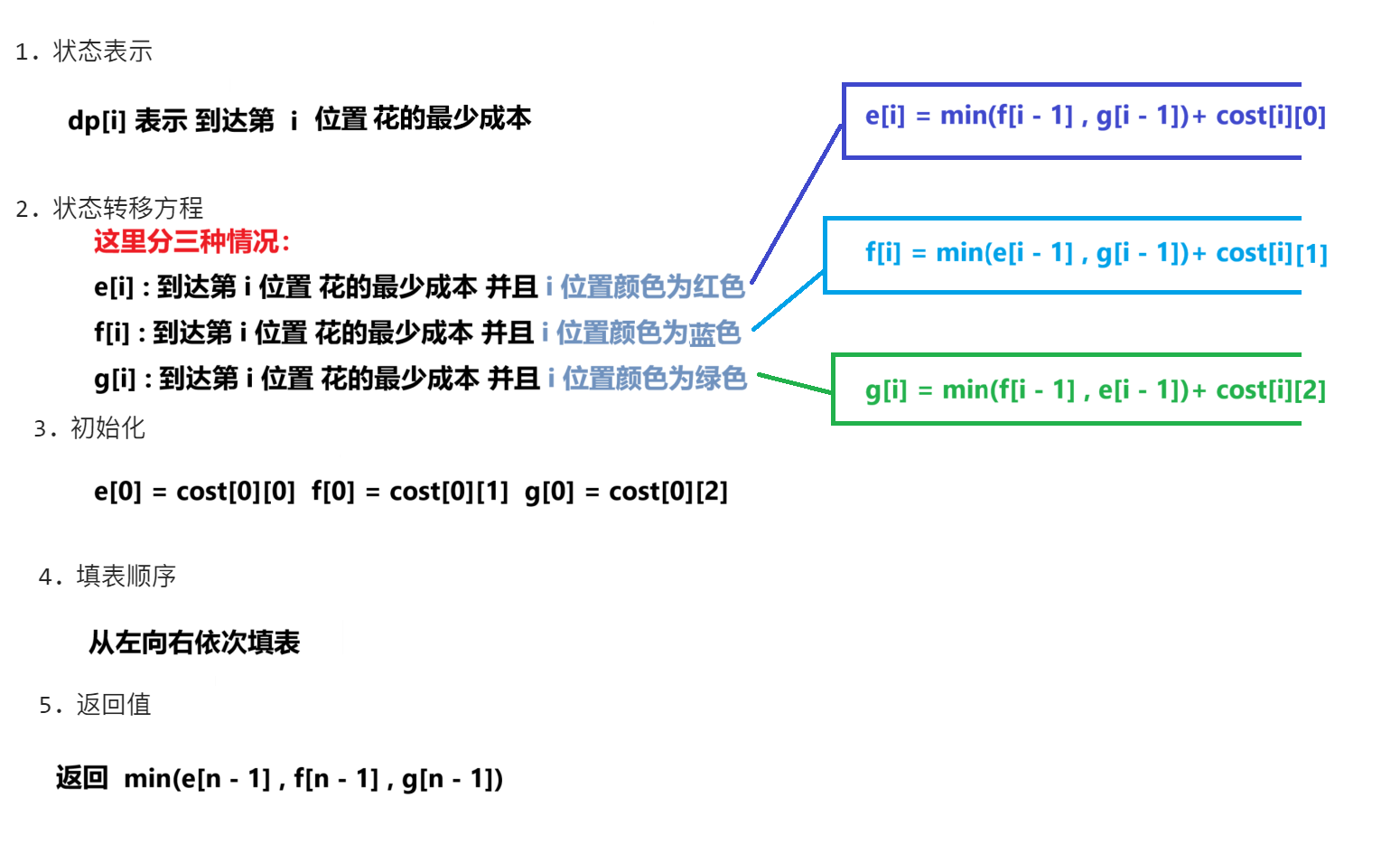
假如有一排房子，共 n 个，每个房子可以被粉刷成红色、蓝色或者绿色这三种颜色中的一种，你需要粉刷所有的房子并且使其相邻的两个房子颜色不能相同。

当然，因为市场上不同颜色油漆的价格不同，所以房子粉刷成不同颜色的花费成本也是不同的。每个房子粉刷成不同颜色的花费是以一个 n x 3 的正整数矩阵 costs 来表示的。

例如，costs[0][0] 表示第 0 号房子粉刷成红色的成本花费；costs[1][2] 表示第 1 号房子粉刷成绿色的花费，以此类推。

请计算出粉刷完所有房子最少的花费成本。

题目链接

LCR 091. 粉刷房子 - 力扣（LeetCode）

文字分析

审题：

相邻房子颜色不一

 代码

class Solution {
public:
    int minCost(vector<vector<int>>& costs) 
    {
       int n = costs.size();
       vector<int> e(n);
       vector<int> f(n);
       vector<int> g(n);
       e[0] = costs[0][0];
       f[0] = costs[0][1];
       g[0] = costs[0][2];
       for(int i = 1;i < n;i++)
       {
         e[i] = costs[i][0] + min(f[i - 1],g[i - 1]);
         f[i] = costs[i][1] + min(e[i - 1],g[i - 1]);
         g[i] = costs[i][2] + min(e[i - 1],f[i - 1]);
       }
       int Min = e[n - 1];
       Min = min(Min,f[n - 1]);
       Min = min(Min,g[n - 1]);
       return Min;
    }
};

14. 309. 买股票的最佳时期含冷冻期

题目：

给定一个整数数组prices，其中第 prices[i] 表示第 i 天的股票价格 。

设计一个算法计算出最大利润。在满足以下约束条件下，你可以尽可能地完成更多的交易（多次买卖一支股票）:

• 卖出股票后，你无法在第二天买入股票 (即冷冻期为 1 天)。

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

题目链接

309. 买卖股票的最佳时机含冷冻期 - 力扣（LeetCode）

文字分析

 代码

class Solution {
public:
    int maxProfit(vector<int>& prices) 
    {
        int n = prices.size();
         vector<vector<int>> dp(n,vector<int>(3));
         dp[0][0] = prices[0] * -1;
         dp[0][1] = 0;
         dp[0][2] = 0;
         for(int i = 1;i < n;i++)
         {
            dp[i][0] = max(dp[i - 1][0],dp[i - 1][1] - prices[i]);
            dp[i][2] = dp[i - 1][0] + prices[i];
            dp[i][1] = max(dp[i - 1][2],dp[i - 1][1]);
         }
         int Max = dp[n - 1][0];
         Max = max(Max,dp[n - 1][1]);
         Max = max(Max,dp[n - 1][2]);
         return Max;

    }
};

15. 714. 买股票的最佳时期含手术费

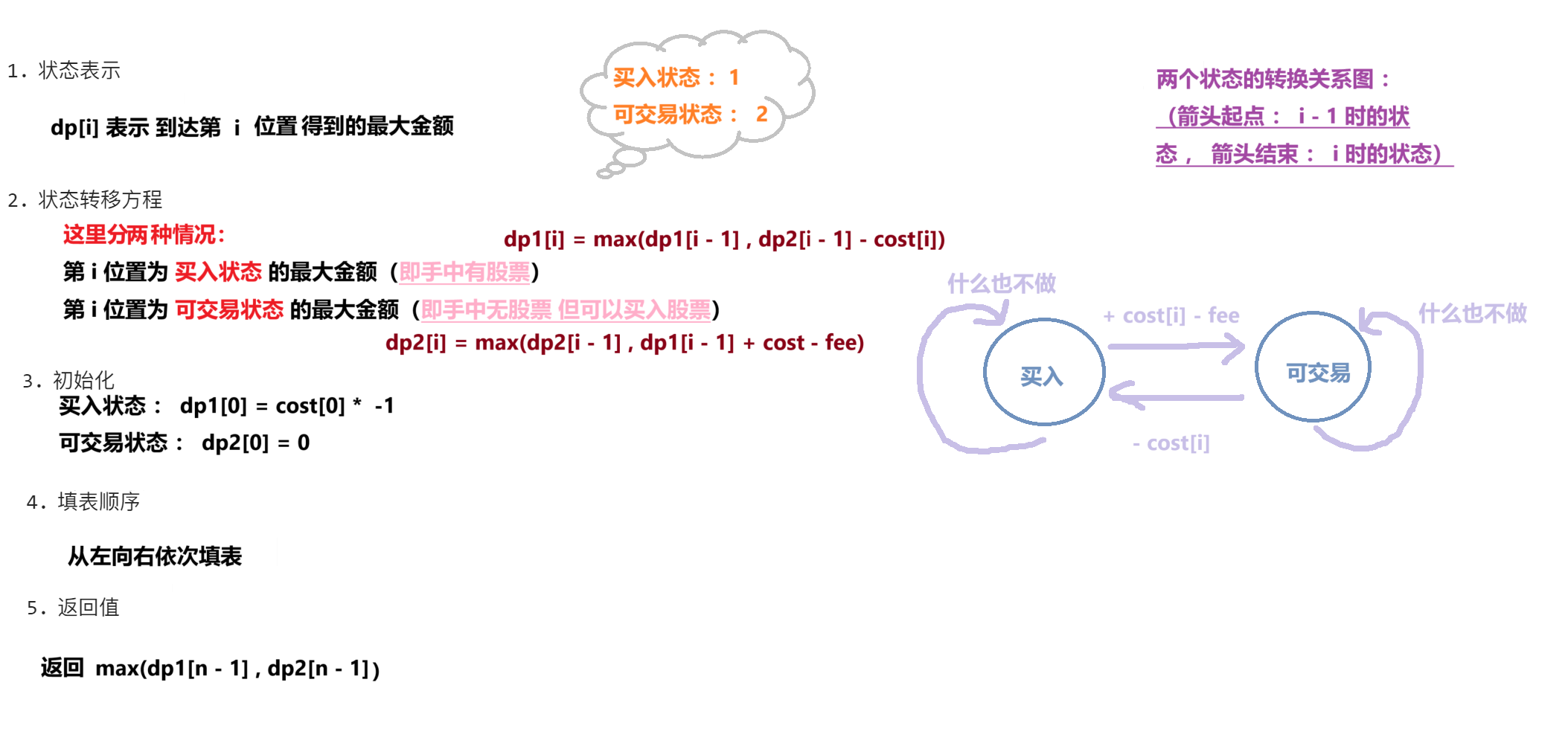
题目：

给定一个整数数组 prices，其中 prices[i]表示第 i 天的股票价格 ；整数 fee 代表了交易股票的手续费用。

你可以无限次地完成交易，但是你每笔交易都需要付手续费。如果你已经购买了一个股票，在卖出它之前你就不能再继续购买股票了。

返回获得利润的最大值。

注意：这里的一笔交易指买入持有并卖出股票的整个过程，每笔交易你只需要为支付一次手续费。给你一个整数数组 nums ，你可以对它进行一些操作。

每次操作中，选择任意一个 nums[i] ，删除它并获得 nums[i] 的点数。之后，你必须删除 所有 等于 nums[i] - 1 和 nums[i] + 1 的元素。

开始你拥有 0 个点数。返回你能通过这些操作获得的最大点数。

题目链接

714. 买卖股票的最佳时机含手续费 - 力扣（LeetCode）

文字分析

审题：

每卖出一次股票后，还要减掉 fee

 代码

class Solution {
public:
    int maxProfit(vector<int>& prices, int fee) 
    {
        int n = prices.size();
        vector<int> dp1(n);
        vector<int> dp2(n);
        dp1[0] = prices[0] * -1;
        dp2[0] = 0;
        for(int i = 1;i < n;i++)
        {
            dp1[i] = max(dp1[i - 1],dp2[i - 1] - prices[i]);
            dp2[i] = max(dp2[i - 1],dp1[i - 1] + prices[i] - fee);
        }
        return max(dp1[n - 1],dp2[n - 1]);
    }
};