Floyd算法求最短路径、娱乐中心选址c++

菜包小姐的先生

已于 2024-06-23 20:29:00 修改

阅读量1k

点赞数 24

文章标签：算法图论

于 2024-05-19 19:46:09 首次发布

本文链接：https://blog.csdn.net/2301_79790771/article/details/139047081

版权

Floyd算法

【问题背景】

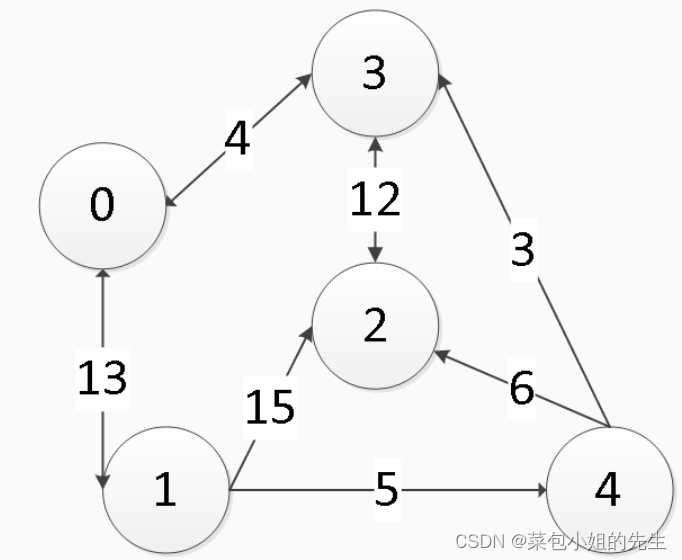
出门旅游，有些城市之间有公路，有些城市之间则没有，如下图。为了节省经费以及方便计划旅程，希望在出发之前知道城市之间的最短路程。

上图中有4个城市8条公路，公路上的数字表示这条公路的长短。请注意这些公路是单向的。我们现在需要求任意两个城市之间的最短路程，也就是求任意两个点之间的最短路径。这个问题这也被称为“多源最短路径”问题。

【Floyd算法思想】

弗洛伊德提出的求每一对顶点之间的最短路径算法。对于网中的任意两个顶点（例如顶点 A 到顶点 B）来说，之间的最短路径不外乎有 2 种情况：

直接从顶点 A 到顶点 B 的弧的权值为顶点 A 到顶点 B 的最短路径；
从顶点 A 开始，经过若干个顶点，最终达到顶点 B，期间经过的弧的权值和为顶点 A 到顶点 B 的最短路径。所以，弗洛伊德算法的核心为：对于从顶点 A 到顶点 B 的最短路径，拿出网中所有的顶点进行如下判断：
Dis（A，K）+ Dis（K，B）< Dis（A，B） Dis（A，K）+ Dis（K，B）< Dis（A，B） K 表示网中所有的顶点；Dis（A，B）表示顶点 A 到顶点 B 的距离。也就是说，拿出所有的顶点 K，判断经过顶点 K 是否存在一条可行路径比直达的路径的权值小，如果式子成立，说明确实存在一条权值更小的路径，此时只需要更新记录的权值和即可。任意的两个顶点全部做以上的判断，最终遍历完成后记录的最终的权值即为对应顶点之间的最短路径。

【Floyd算法实现】

对上图创建distance和path两个二维数组，记录两个顶点之间的距离和路径，在算法进行中，对两个二维数组进行更新，最后得到任意两个顶点之间的最短路径。

【伪代码】

1. 初始化距离数组dist，路径数组path

2 进行VNum次的更新

2.1 更新两个二维矩阵，取出dist矩阵中的每一个元素，与同一行第k列，同一列第k行的元素之和相比较

2.2 考虑通过第k顶点，从i到k 从k到j，是否拉近了i j 之间的距离

2.3 如果拉近了距离，就更新dist和path两个数组 3 输出结果

【输入输出】

第一行输入顶点和边的个数vertexNum和arcNum

第二行输入顶点的值

下面多行输入边的起点和终点的值，边的权值。

【测试数据1】

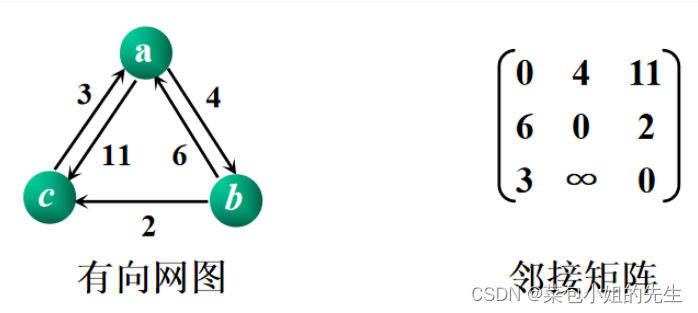
请输入顶点个数和边的个数：3 5

请输入顶点的值a b c

请输入边依附的两个顶点和权值:

a b 4

b a 6

b c 2

c a 3

a c 11

显示每对顶点间的最短路径：

<a,b> 的最短路径为：ab 最短路径长度为：4

<a,c> 的最短路径为：abc 最短路径长度为：6

<b,a> 的最短路径为：bca 最短路径长度为：5

<b,c> 的最短路径为：bc 最短路径长度为：2

<c,a> 的最短路径为：ca 最短路径长度为：3

<c,b> 的最短路径为：cab 最短路径长度为：7

【测试数据2】

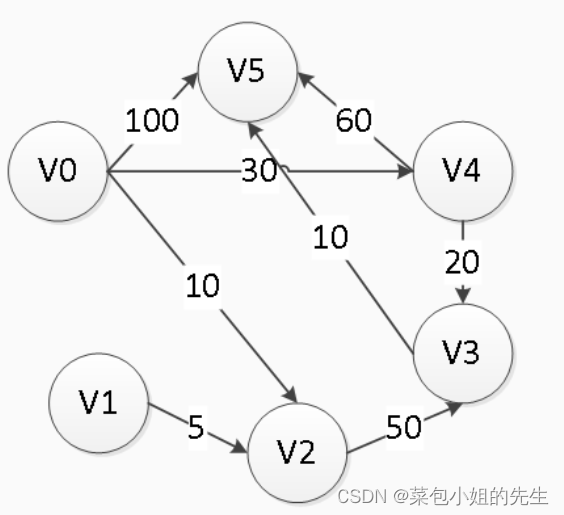
请输入顶点个数和边的个数：6 8

请输入顶点的值0 1 2 3 4 5

请输入边依附的两个顶点和权值:

0 4 30

0 5 100

0 2 10

1 2 5

2 3 50

3 5 10

4 3 20

4 5 60

显示每对顶点间的最短路径：

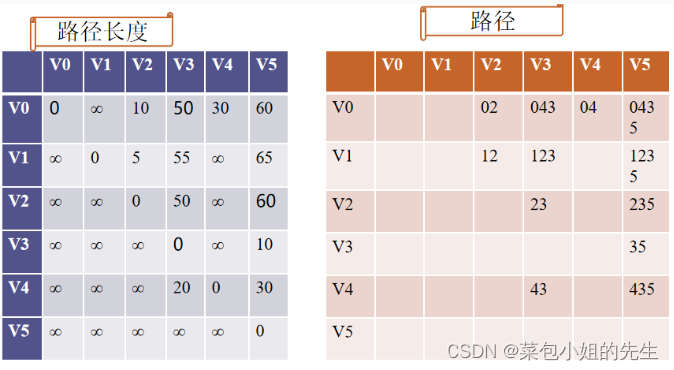
<0,1> 无路径

<0,2> 的最短路径为：02 最短路径长度为：10

<0,3> 的最短路径为：043 最短路径长度为：50

<0,4> 的最短路径为：04 最短路径长度为：30

<0,5> 的最短路径为：0435 最短路径长度为：60

<1,0> 无路径

<1,2> 的最短路径为：12 最短路径长度为：5

<1,3> 的最短路径为：123 最短路径长度为：55

<1,4> 无路径

<1,5> 的最短路径为：1235 最短路径长度为：65

<2,0> 无路径

<2,1> 无路径

<2,3> 的最短路径为：23 最短路径长度为：50

<2,4> 无路径

<2,5> 的最短路径为：235 最短路径长度为：60

<3,0> 无路径

<3,1> 无路径

<3,2> 无路径

<3,4> 无路径

<3,5> 的最短路径为：35 最短路径长度为：10

<4,0> 无路径

<4,1> 无路径

<4,2> 无路径

<4,3> 的最短路径为：43 最短路径长度为：20

<4,5> 的最短路径为：435 最短路径长度为：30

<5,0> 无路径

<5,1> 无路径

<5,2> 无路径

<5,3> 无路径

<5,4> 无路径

【代码】

#include<iostream>
#include<algorithm>
#include<string>
#include<limits.h>
using namespace std;
const int MAX_V_NUM = 100;


template <class T>
class EdgeGraph
{
private:
	char vertex[MAX_V_NUM] = { 0 };  //存放图顶点的数组
	int dist[MAX_V_NUM][MAX_V_NUM] = { INT_MAX };
	string path[MAX_V_NUM][MAX_V_NUM]; //用来存放路径
	int vexNum, arcNum;         //图的顶点数和边数
public:
	EdgeGraph(int vNum, int eNum);//构造函数
	void Floyd();
	int getIndex(char v)
	{
		for (int i = 0; i < vexNum; i++) {
			if (vertex[i] == v) {
				return i;
			}
		}
		return -1; // 如果找不到顶点，返回-1
	}
	//路径拼接函数，需要将传入的a末尾和b的开头部分的重复字母处理一下，拼成新的路径。比如：a是abc，b是cde，result是abcde，重复的c只存入了一次
	string Combine(string a, string b)
	{
		if (a == b)
			return   "";
		else {
			string result;
			result.resize(a.length() + b.length()); // 预先分配足够的空间,没有分配空间就无法返回正确的字符串
			int index = 0;
			int inda = 0, indb = 0;
			while (inda < a.length()) //先将a串存入result
			{
				result[index++] = a[inda++];
			}
			indb++; //跳过b串的第一个字符
			while (indb < b.length()) //将b后面的内容存入result
			{
				result[index++] = b[indb++];
			}
			result[index] = '\0'; //结束
			return result;
		}
	}
};
template <class T>
EdgeGraph<T>::EdgeGraph(int vNum, int eNum)
{
	vexNum = vNum;
	arcNum = eNum;
	//dist数组的初始化，让对角线上为0，其余为无穷大
	for (int i = 0; i < vexNum; i++)
	{
		for (int j = 0; j < vexNum; j++)
		{
			if (i == j)
				dist[i][j] = 0;
			else
				dist[i][j] = INT_MAX;
		}
	}
	char v;
	T f, t;
	int w;
	cout << "请输入顶点的值";
	for (int i = 0; i < vexNum; i++)
	{
		cin >> v;
		vertex[i] = v;
	}

	cout << "请输入边依附的两个顶点和权值:\n";
	for (int i = 0; i < arcNum; i++)
	{
		cin >> f;
		cin >> t;
		cin >> w;
		dist[getIndex(f)][getIndex(t)] = w;
	}
}
template <class T>
void EdgeGraph<T>::Floyd()
{
	//初始化path
	for (int i = 0; i < vexNum; i++)
	{
		for (int j = 0; j < vexNum; j++)
		{
			if (dist[i][j] != INT_MAX && dist[i][j] != 0) //如果两个地点有路线连接，并且起点和终点不是同一个位置
			{
				path[i][j] = { vertex[i],vertex[j] }; //把起始位置和终点位置拼成一个字符串，存入path 中
			}
			else
				path[i][j] = "";  //否则path中存空
		}
	}

	//开始查找
	string result; //记录路径结果
	for (int k = 0; k < vexNum; k++)
	{
		for (int i = 0; i < vexNum; i++)
		{
			for (int j = 0; j < vexNum; j++)
			{
				if (dist[i][k] + dist[k][j] < dist[i][j] && dist[i][k] != INT_MAX && dist[k][j] != INT_MAX) //当找到更短的路径
				{
					dist[i][j] = dist[i][k] + dist[k][j]; //更新短路径
					result = Combine(path[i][k], path[k][j]);  //并记录path，存入到path数组中
					path[i][j] = result;
				}
			}
		}
	}
	//输出
	cout << "显示每对顶点间的最短路径：" << endl;
	for (int i = 0; i < vexNum; ++i) {
		for (int j = 0; j < vexNum; ++j) {
			if (i == j)
				continue;
			else {
				if (dist[i][j] == INT_MAX) {
					cout << "<" << vertex[i] << "," << vertex[j] << "> 无路径";
					if (i < arcNum-1)
						cout << endl;
				}
				else {
					cout << "<" << vertex[i] << "," << vertex[j] << "> 的最短路径为：" << path[i][j] << " 最短路径长度为：" << dist[i][j];
					if (i < arcNum-1)
						cout << endl;
				}				
			}
		}
	}
}

int main()
{
	int vNum, eNum;
	cout << "请输入顶点个数和边的个数：";
	cin >> vNum >> eNum;
	EdgeGraph<char> graph(vNum, eNum);
	graph.Floyd();
	return 0;
}

娱乐中心选址

【问题描述】

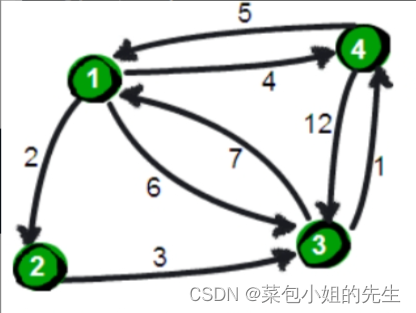
有向图的邻接矩阵如下图，建娱乐中心，要求娱乐中心距其它顶点的最长往返路径最短，相同条件下总的往返路径越短越好，如何选址？

娱乐中心选址问题的有向图：

有向图的邻接矩阵：

【思路提示】

娱乐中心选址问题实际是求有向图中心点的问题。

【伪代码】

娱乐中心选址问题的算法用伪代码描述如下：

1．对加权有（无）向图，调用Floyd算法，求每对顶点间最短路径长度的矩阵；

2．对最短路径长度矩阵的每行求和；

3．找到和的最小值所在行，对应的地点可选为中心点。

上图的dist矩阵计算得出是：

0 13 16 4 18

12 0 11 8 5

16 29 0 12 34

4 17 12 0 22

7 20 6 3 0

对矩阵的每一行求和，找到和的最小值为1行。因此，选址地点为1，最短路径长度为36。

【输入输出】

第一行输入顶点数量和边的数量，注意是有向图。

下面多行输入每个边的起点编号，终点编号和权值，注意是有向图。

输出选址地点和最短路径的长度

【测试数据】

输入：

5 10

0 3 4

3 0 4

0 1 13

1 0 13

1 2 15

1 4 5

4 2 6

4 3 3

2 3 12

3 2 12

输出

选址地点为1

最短路径长度为36

【代码】

#include<iostream>
#include<algorithm>
#include<string>
#include<limits.h>
using namespace std;
const int MAX_V_NUM = 100;


template <class T>
class EdgeGraph
{
private:
	char vertex[MAX_V_NUM] = { 0 };  //存放图顶点的数组
	int dist[MAX_V_NUM][MAX_V_NUM] = { INT_MAX };
	string path[MAX_V_NUM][MAX_V_NUM]; //用来存放路径
	int vexNum, arcNum;         //图的顶点数和边数
	int shortP[MAX_V_NUM];
	int newdist[MAX_V_NUM][MAX_V_NUM];
public:
	EdgeGraph(int vNum, int eNum);//构造函数
	void Floyd();
	void getShortPath();  //存储每对顶点的最短路径
	int getIndex(char v)
	{
		for (int i = 0; i < vexNum; i++) {
			if (vertex[i] == v) {
				return i;
			}
		}
		return -1; // 如果找不到顶点，返回-1
	}
	//路径拼接函数，需要将传入的a末尾和b的开头部分的重复字母处理一下，拼成新的路径。比如：a是abc，b是cde，result是abcde，重复的c只存入了一次
	string Combine(string a, string b)
	{
		if (a == b)
			return   "";
		else {
			string result;
			result.resize(a.length() + b.length()); // 预先分配足够的空间,没有分配空间就无法返回正确的字符串
			int index = 0;
			int inda = 0, indb = 0;
			while (inda < a.length()) //先将a串存入result
			{
				result[index++] = a[inda++];
			}
			indb++; //跳过b串的第一个字符
			while (indb < b.length()) //将b后面的内容存入result
			{
				result[index++] = b[indb++];
			}
			result[index] = '\0'; //结束
			return result;
		}
	}
};
template <class T>
EdgeGraph<T>::EdgeGraph(int vNum, int eNum)
{
	vexNum = vNum;
	arcNum = eNum;
	//dist数组的初始化，让对角线上为0，其余为无穷大
	for (int i = 0; i < vexNum; i++)
	{
		for (int j = 0; j < vexNum; j++)
		{
			if (i == j)
			{
				dist[i][j] = 0;
				newdist[i][j] = 0;
			}
			else
			{
				dist[i][j] = INT_MAX;
				newdist[i][j] = INT_MAX;
			}
		}
	}
	T f, t;
	int w;
	//顶点的初始化
	for (int i = 0; i < vexNum; i++)
	{
		vertex[i] = i+'0';  //这里得转化一下，当成字符
	}
	//short数组的初始化
	for (int i = 0; i < vexNum; i++)
	{
		
			shortP[i] = 0;
	}
	//cout << "请输入边依附的两个顶点和权值:\n";
	for (int i = 0; i < arcNum; i++)
	{
		cin >> f;
		cin >> t;
		cin >> w;
		dist[getIndex(f)][getIndex(t)] = w;
	}
	
}
template <class T>
void EdgeGraph<T>::Floyd()
{
	//初始化path
	for (int i = 0; i < vexNum; i++)
	{
		for (int j = 0; j < vexNum; j++)
		{
			if (dist[i][j] != INT_MAX && dist[i][j] != 0) //如果两个地点有路线连接，并且起点和终点不是同一个位置
			{
				path[i][j] = { vertex[i],vertex[j] }; //把起始位置和终点位置拼成一个字符串，存入path 中
			}
			else
				path[i][j] = "";  //否则path中存空
		}
	}

	//开始查找
	string result; //记录路径结果
	for (int k = 0; k < vexNum; k++)
	{
		for (int i = 0; i < vexNum; i++)
		{
			for (int j = 0; j < vexNum; j++)
			{
				if (dist[i][k] + dist[k][j] < dist[i][j] && dist[i][k] != INT_MAX && dist[k][j] != INT_MAX) //当找到更短的路径
				{
					dist[i][j] = dist[i][k] + dist[k][j]; //更新短路径
					result = Combine(path[i][k], path[k][j]);  //并记录path，存入到path数组中
					path[i][j] = result;
				}
			}
		}
	}
	//输出
	//cout << "显示每对顶点间的最短路径：" << endl;
	for (int i = 0; i < vexNum; ++i) {
		for (int j = 0; j < vexNum; ++j) {
			if (i == j)
				continue;
			else {
				if (dist[i][j] == INT_MAX) {
					newdist[i][j]= INT_MAX;
				}
				else {
					newdist[i][j]=dist[i][j];
				}				
			}
		}
	}
}
//调用Floyd算法，求每对顶点间最短路径长度的矩阵；
template <class T>
void EdgeGraph<T>::getShortPath()
{
	Floyd();
	
	for (int i = 0; i < vexNum; i++)
	{
		for (int j = 0; j < vexNum; j++)
		{
			if (newdist[i][j] != INT_MAX)
				shortP[i] += newdist[i][j];
			else
			{
				shortP[i] = INT_MAX;
				break;
			}
		}
	}
	int min = INT_MAX,index=0;
	for (int i = 0; i < vexNum; i++)
	{
		if (shortP[i] < min)
		{
			min = shortP[i];
			index = i;
		}
	}
	cout << "选址地点为" << index <<endl;
	cout << "最短路径长度为" << shortP[index];
}
int main()
{
	int vNum, eNum;
	//cout << "请输入顶点个数和边的个数：";
	cin >> vNum >> eNum;
	EdgeGraph<char> graph(vNum, eNum);
	graph.getShortPath();
	return 0;
}

菜包小姐的先生

关注

24
点赞
踩
20

收藏

觉得还不错? 一键收藏
1
评论
Floyd算法求最短路径、娱乐中心选址c++

对上图创建distance和path两个二维数组，记录两个顶点之间的距离和路径，在算法进行中，对两个二维数组进行更新，最后得到任意两个顶点之间的最短路径。的最短路径为：0435 最短路径长度为：60。的最短路径为：043 最短路径长度为：50。的最短路径为：235 最短路径长度为：60。的最短路径为：435 最短路径长度为：30。的最短路径为：bca 最短路径长度为：5。的最短路径为：23 最短路径长度为：50。
复制链接

扫一扫