机器学习基础（第一章）

机器学习第一章¹

1. 机器学习基本概念

2.机器学习的种类

1. **regression（回归）**即为输出预测的函数值
2. **classification（分类）：**多适用于做选择
3. **Structured Learning（结构化学习）：**让机器学会创造

3.机器学习的步骤

3.1 Function with Unknown Parameters（未知参数函数）

$$y=b+w{x}_1$$

b与w是未知的，称为参数（parameter）

这个带有Unknown的Parameter的Function，称之为Model（模型）

x1在这个Function中是已知的，是前一天的后台数据，称之为Feature（特征）

w是与Feature相乘的数，称之为weight（权重）

b没有与feature相乘，称之为Bias（偏离率）

3.2 Define Loss from Training Data（定义训练数据的损失函数）

根据训练资料，定义loss函数，用来衡量函数解和真实情况的差距。

**Loss：**是关于选取未知参数后的函数，不同参数的选择从而产生不同的函数，计算出不一样的Loss，而Loss的作用就是用来评估这些未知参数的选取好还是不好。

L越大，代表当前的参数值的选取越不好；L的值越小，代表当前的这一组参数的选取越好。

在之前的吴恩达深度学习中你已经学过了。试着想想。

3.3 Error Surface（误差曲面）

该图为一个真实数据计算出来的结果，我们可以调整b和w，让其取不同的值，每种组合都计算其Loss的值，画下其等高线图（Error Surface）。

在这个等高线图上面，越偏红色系，代表计算出来的Loss越大，就代表这一组w跟b未知参数的选取越差；如果越偏蓝色系，Loss越小，就代表这一组w跟b未知参数的选择越好。

3.4 Optimization（最优化）

最优化的目的就是找到使 loss最小的参数。

也就是找到一个合适的w与b，可以让Loss的值最小，我们让这两个合适的参数称为w**和b*。*

即为上图中蓝色区域最深的地方。

至于优化方法，还是熟悉的Gradient Descent(梯度下降)。

1. 取w0和b0；（并不一定随机，有选择的方法）；

2. 分别对损失函数取w和b的偏导；

3. 若在某点w和b的值为负（即偏导为负值），则令w和b增加不同的η（Learning rate，学习率）；若在某点为正，则令w或者b减少η；重复上述操作。

4. 找到相应的w和b偏导的零值，此处即为loss的最低阈值。

**Learning rate（学习率）**是影响w移动步长的重要因素，令学习速率为η。

η的值越大，w参数每次update到下一个位置的步长幅度就会越大；

η的值很小，则参数update就会很慢，每次只会改一点点参数的值。

（这类需要人手工设置的参数叫做hyperparameters 超参数）

其公式为
$$w^1\leftarrow w^0-\eta \frac{\partial L}{\partial w}{|}_{w_0}$$
其中learning rate需要乘以前一参数的微分，再进行相减操作。即为
$$w^{n+1}\leftarrow w^n-\eta \frac{\partial L}{\partial w}{|}_{w^n}$$
不断进行更新。

不难看出，当函数的微分$\frac{\partial L}{\partial w}{|}_{w^n}$为负值时，代表斜率为负，乘以减号和 $\eta$ 刚好进行相加操作；反之斜率为正，将会对参数进行相减操作，使函数斜率不断朝零靠拢。

但是该方法也有一个缺点，因为停下来有两种情况：

1. 在计算微分的时候操作者已经设置了更新次数的上限制，例如update达到100万次以后就不会再更新。
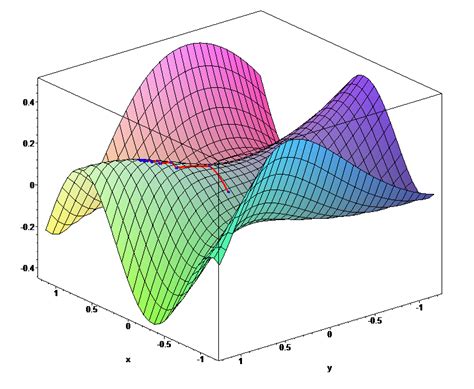
2. 代表斜率已经为0，最好的情况是已经到达了global minima（全局最小值），使得Loss减小到了最小值。 但也无法分辨是否是达到了不好的情况，即：停止点仅仅是local minima（局部最小值），还没有到达Loss最低值，但更新操作已提前结束。如图所示。

4. 如何表示更复杂的模型

$$y=wx+b$$只是一条直线，无法拟合更复杂的关系。

**
**

图 线性模型的局限性

如图所示，$$y=wx+b$$只能表示一条直线，改变w和b只能改变斜率和y的交点位置。若想拟合更加复杂的曲线（如图中红色曲线），可直观地看出无法拟合。

接下来，将讨论可能会面临的更复杂的关系，以及如何拟合这些复杂关系。

4.1 单变量：如何表示连续曲线

图 分段曲线可以逼近任何连续曲线

如图所示，这是一条光滑的曲线。

如何去拟合它呢？

充足的线性分段曲线可以逼近连续曲线。

因此可以使用分段线性曲线（Piecewise Linear Curves）。

4.1.1 分段线性曲线（Piecewise Linear Curves）

![在这里插入图片描述](https://i-blog.csdnimg.cn/direct/c9111caf4e56432abbdb9778368f9742.png

如图所示。

红色曲线（red curve）为分段线性曲线，蓝线是不同的hard sigmoid曲线。一组hard sigmoid曲线再加上常数可以

组成任何分段线性曲线（Piecewise Linear Curves）。

需要注意的是，hard sigmoid函数不能作为基础函数，因为转角处无法求微分，我们需要hard sigmoid曲线的近似曲线

*** sigmoid*** 作为基础函数。

如图所示。

图 使用sigmoid 逼近hard sigmoid

4.2.2 Sigmoid function

其公式为
$$\begin{gathered} y=c\frac{1}{1+e^{-(b+w{x}_1)}} \\ =c\ast sigmiod(b+w{x}_1) \end{gathered}$$
c、b、w各有不同的作用。

通过改变$$c、b、w$$，可以拟合不同的hard sigmoid。

总结

通过sigmoid函数代表hard sigmoid，由不同的hard sigmoid组成分段线性曲线，进而拟合任何光滑曲线。

最终，分段线性曲线的公式为
$$y=b+\sum _i{c}_i\sigma (b_i+w_i{x}_1)$$

b为常数，公式后半部为sigmoid函数的加和。

注意
$$\sigma =sigmoid$$

4.2 多变量：如何表示更复杂的模型

我们可以不止用一个特征$$x_1$$，可以用多个特征带入不同的$$c,b,w$$​，从而得到更有灵活性（flexibility）的函数，如图所示。用 $$j$$ 来代表特征（feature）的编号。如果要考虑前 28 天， $$j$$ 就是 1 到 28。

图 构建更有灵活性的函数

将 $$j$$ 设为3，$$x_1$$、$$x_2$$、$$x_3$$分别为三天的数据，如图所示，每一个 $$i$$ 就代表一个蓝色的函数。

每一个蓝色的函数都用一个 Sigmoid 函数来比近似它，序号①、②、③代表有个 Sigmoid 函数。

注意区分单变量与多变量的区别：

• 特征 $$x$$ 唯一。通过改变sigmoid函数中的 $$c、w、b$$ ，表示不同的hard sigmoid函数，进而表示分段线性函数。
• 特征 $$x$$ 不唯一，$$c、w、b$$ 也不唯一。例如，一个特征$$x_1$$有不同的 $$c_i、w_i、b_i$$ 对应，衍生出不同的sigmoid函数，$$x_2、x_3$$​类似。

多变量中，通过公式
$$y=b+\sum _i{c}_i\sigma (b_i+\sum _j{w}_{ij}{x}_j)$$
拟合，$$w_{ij}$$ 代表在第 $$i$$ 个sigmoid中乘给第 $$j$$ 个特征的权重。

设共有3个sigmoid，则第一个sigmoid需计算的值
$$r_i=b_i+\sum _j{w}_{ij}{x}_j$$
即为
$$r_1=b_1+w_{11}{x}_1+w_{12}{x}_2+w_{13}{x}_3$$
同理可得
$$\begin{gathered} r_1=b_1+w_{11}{x}_1+w_{12}{x}_2+w_{13}{x}_3 \\ {r}_2=b_2+w_{21}{x}_1+w_{22}{x}_2+w_{23}{x}_3 \\ {r}_3=b_3+w_{31}{x}_1+w_{32}{x}_2+w_{33}{x}_3 \end{gathered}$$
化为线性代数的计算方法
$$\left[\begin{array}{c}{r}_1\\ r_2\\ r_3\end{array}\right]=\left[\begin{array}{c}{b}_1\\ b_2\\ b_3\end{array}\right]+\left[\begin{array}{ccc}{w}_{11}& w_{12}& w_{13}\\ w_{21}& w_{22}& w_{23}\\ w_{31}& w_{32}& w_{33}\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\\ x_3\end{array}\right]$$

$$\Updownarrow$$

$$\mathbf{r}=\mathbf{b}+\mathbf{Wx}$$

具体的计算过程如图所示

图 比较有灵活性函数（多变量函数）的计算过程

其中：a为 $$\sigma (r)$$​ 。

将函数再次抽象为

• 对此图的解释：在该函数中，$$W、b、c^T、b$$ 统称为未知参数。将未知参数向量化展开，展开成如图的色块（$$W$$的展开方式可以是整行也可以是整列），将这些展开的向量“拼”在一起，形成一个新的向量，这个新的向量也就是包含位置参数的向量称为 $\theta$​ 。

$$\theta =\left[\begin{array}{c}{\theta }_1\\ {\theta }_2\\ {\theta }_3\\ ⋮\end{array}\right]$$

4.2.1 多变量的Optimization

之前的损失函数$L(w,b)$在多变量中表示为 $L(\theta )$。设一组初始 $\theta$ 数值为 ${\theta }^0$ ,经最优化操作后的未知数向量为 ${\theta }^{\ast }$ 。

由 **3.4 Optimization（最优化）**可知，求多变量的Loss函数最小值核心思想仍为
$${\theta }^{n+1}\leftarrow {\theta }^n-\eta g^n$$

其中 $g$ 为 $L$ 对 $\theta$ 中不同未知数的微分（与 $L(w,b)$ 一样，均为分别求未知数的微分，然后通过梯度下降找出最优解。不同之处为未知数数量 $\theta$​ 更多）

设 $\theta$ 的上标为同一组向量的批次， $\theta$ 的下标为该批次向量中的未知数。如下公式所示。
$${\theta }^1=\left[\begin{array}{c}{\theta }_1^1\\ {\theta }_2^1\\ {\theta }_3^1\\ ⋮\end{array}\right]$$
上标为1，表示这是第1批次的 $\theta$ ；下标为1，2，3…表示在该批次的 $\theta$ 向量中，不同的未知数。
$$g=\left[\begin{array}{c}\frac{\partial L}{\partial {\theta }_1}{|}_{\theta ={\theta }_1^n}\\ \frac{\partial L}{\partial {\theta }_2}{|}_{\theta ={\theta }_2^n}\\ \frac{\partial L}{\partial {\theta }_3}{|}_{\theta ={\theta }_3^n}\\ ⋮\end{array}\right]$$
g的含义为：在 $L$ 中分别对 $\theta$ 中的所有未知数求偏导，再将现批次的 $\theta$ 中的值代入。

完整的公式为
$$\left[\begin{array}{c}{\theta }_1^{n+1}\\ {\theta }_2^{n+1}\\ {\theta }_3^{n+1}\\ ⋮\end{array}\right]\leftarrow \left[\begin{array}{c}{\theta }_1^n\\ {\theta }_2^n\\ {\theta }_3^n\\ ⋮\end{array}\right]-\eta \left[\begin{array}{c}\frac{\partial L}{\partial {\theta }_1}{|}_{\theta ={\theta }_1^n}\\ \frac{\partial L}{\partial {\theta }_2}{|}_{\theta ={\theta }_2^n}\\ \frac{\partial L}{\partial {\theta }_3}{|}_{\theta ={\theta }_3^n}\\ ⋮\end{array}\right]$$

$$\Updownarrow$$

$${\theta }^{n+1}\leftarrow {\theta }^n-\eta g^n$$

4.2.2 批处理

笔者写不动了…光是公式笔者就敲了大半天，后续的批处理及更往后的几章，就静静等待后续更新。

有什么错误、改进的地方，欢迎各位大佬指正。

over –

---

---

1. written by Shepherd in 7&8/24,main references: leedl-tutorial ;zyd机器学习笔记 ↩︎