数字图像处理实验2_实验2数字图像基本运算-CSDN博客

本文链接：https://blog.csdn.net/2301_79902171/article/details/146571270

一、点运算（图像灰度变换）

点运算是针对每个像素点上的灰度值进行运算，从而得到新的符合需求的图像。简单最具有代表性的图像处理方法,该方法不改变图像像素点之间的位置关系，灰度值,因此又称灰度变换。

从数学角度来看，点运算通常可以分为线性点运算和非线性点运算。

1.线性点运算

利用线性方程s=ar+b来完成对图像的点运算，s为输出灰度值,r 为输入灰度值,a 和b 为变换系数。
通过调整a和b的取值,可以得到不同的变换效果:

当a=1,b=0时,输入和输出相等,即输出原图像。
当a=1,b>0时,输出灰度值变大,图像整体变亮。
当a=1,b<0时,输出灰度值变小,图像整体变暗。
当a>1时,输出图像对比度增大。
当0<a<1时,输出图像对比度减小。
当a<0时,图像暗区变亮,亮区变暗,完成图像求补。

运行代码如下：

# 导入库
import matplotlib.pyplot as plt  # 用于绘图和显示图像
import cv2  # OpenCV库，用于图像处理

# 读取图像，0表示以灰度模式读取
img = cv2.imread('D:\\MyDIP\\001.bmp', 0)

# 定义线性变换函数：img1 = a * img + b
# 通过不同的a和b值，我们可以调整图像的亮度和对比度

# 设置不同的a和b值，并应用线性变换
a, b = 1, 0
img1 = cv2.add(cv2.multiply(a, img), b)  # 使用OpenCV的函数进行安全的算术运算

# 使用matplotlib创建子图来展示不同参数下的变换效果
plt.subplot(231)  # 2行3列的第1个子图
plt.imshow(img1, 'gray')  # 显示灰度图像
plt.title('a=1,b=0')  # 设置子图标题

# 重复上述过程，使用不同的a和b值
a, b = 1, 50
img1 = cv2.add(cv2.multiply(a, img), b)
plt.subplot(232)
plt.imshow(img1, 'gray')
plt.title('a=1,b=50')

a, b = 1, -50
img1 = cv2.add(cv2.multiply(a, img), b)
plt.subplot(233)
plt.imshow(img1, 'gray')
plt.title('a=1,b=-50')

a, b = 1.5, 0
img1 = cv2.add(cv2.multiply(a, img), b)
plt.subplot(234)
plt.imshow(img1, 'gray')
plt.title('a=1.5,b=0')

a, b = 0.3, 0
img1 = cv2.add(cv2.multiply(a, img), b)
plt.subplot(235)
plt.imshow(img1, 'gray')
plt.title('a=0.3,b=0')

a, b = -1, 0
img1 = a * img + b  # 这里直接进行算术运算，注意可能的数据溢出问题
plt.subplot(236)
plt.imshow(img1, 'gray')
plt.title('a=-1,b=0')

# 显示
plt.show()

运行结果：

2.非线性点运算

非线性点运算有两种，分别是对数运算和幂次运算。其中幂次变换比对数变换更加复杂。于是我们便用幂次变化对图像进行处理。
指数方程为 $s=cr**γ$ ，s为输出灰度值,r 为输入灰度值,c 和γ 为正常数，γ 值以1为分界线,当值大于1时,可以产生和对数运算相同的结果,即将灰度值低的区域进行扩展,灰度值高的区域进行压缩,提高图像亮度;当γ 值小于1时,将得到相反的结果,即灰度值高的区域进行扩展,将灰度值低的区域进行压缩,减小图像亮度;当c=γ=1是,将是简单的线性变换,输入与输出相等。

运行代码如下：

# 导入所需库
import cv2
import matplotlib.pyplot as plt

# 读取灰度图像并归一化
img = cv2.imread('D:\\MyDIP\\001.bmp', 0)
img = img / 255.0

# 创建子图显示原始图像
plt.subplot(231)
plt.imshow(img, 'gray')
plt.title('Original Image')
# 设置不同幂次参数并显示变换结果
r=0.1
plt.subplot(232) # 创建对应子图
temp=cv2. pow(img,0.1)# 应用幂次变换
plt. imshow(temp,'gray')# 显示变换后的图像
plt. title('c=1,r=0. 1') # 设置子图标题

r=0.4
plt. subplot (233)
temp-cv2. pow(img,0.4)
plt. imshow (temp,'gray')
plt. title('c=1,r=0. 4')

r=1
plt. subplot(234)
temp=cv2. pow (img,1)
plt. imshow (temp,'gray')
plt. title('c=1,r=1')

r=2.5
plt. subplot(235)
temp-cv2. pow(img,2.5)
plt. imshow (temp,'gray')
plt. title('c=1,r=2. 5')

r=10
plt. subplot(236)
temp=cv2. pow(img,10)
plt. imshow (temp,'gray')
plt. title('c-1,r=10')
plt. show()

运行结果：

二、代数运算

代数运算是对两幅或者两幅以上的图像进行加、减、乘、除运算，从而得到预期的结果。

1.加法运算

加法运算通常用来去除加性噪声,因为当噪声可以用一个独立分布的随机模型表示和描述时,就可以利用平均值方法减低信号的噪声。
运行代码如下：

# 导入库
import numpy as np
import cv2
import matplotlib.pyplot as plt


# 设置中文字体为黑体
plt.rcParams['font.sans-serif'] = ['SimHei']
# 解决负号显示问题
plt.rcParams['axes.unicode_minus'] = False
def GaussianNoise(image, mean, var):
    """
    为输入图像添加高斯噪声
    参数:
        image: 输入图像（需为numpy数组）
        mean: 噪声均值
        var: 噪声方差
    返回:
        noisy: 添加噪声后的图像（值域[0,1]）
    """
    row, col = image.shape
    sigma = var ** 0.5  # 计算标准差
    gauss = np.random.normal(mean, sigma, (row, col))  # 生成高斯噪声
    noisy = image + gauss  # 添加噪声
    noisy = np.clip(noisy, 0, 1)  # 将值限制在[0,1]范围内
    return noisy


# 读取图像并转换为numpy数组
img = cv2.imread('D:\\MyDIP\\001.bmp', 0)
img = np.array(img)
img.flags.writeable = True  # 确保数组可写
img = img / 255  # 归一化到[0,1]范围

# 添加高斯噪声（均值0，方差0.05）
img_n = GaussianNoise(img, 0, 0.05)

# 创建子图显示原始图像和单次噪声图像
plt.subplot(131)
plt.imshow(img, 'gray')
plt.title('原图')

plt.subplot(132)
plt.imshow(img_n, 'gray')
plt.title('带噪声图片')

# 多次添加噪声并取平均
k = np.zeros([img.shape[0], img.shape[1]])  # 初始化累加器
for i in range(100):
    j = GaussianNoise(img, 0, 0.05)  # 生成噪声图像
    k = k + j  # 累加噪声图像
k = k / 100  # 计算平均值

# 显示最终平均结果
plt.subplot(133)
plt.imshow(k, 'gray')
plt.title('去噪声图片')

plt.show()

运行结果：

2.减法运算

常用来检测变化和运动的物体,又称差分运算。将同一景物不同时间拍摄的图像进行减法运算,可以实现对该区域的动态监测、运动目标检测和跟踪等操作。

运行代码如下：

# 导入库
import numpy as np
import cv2
import matplotlib.pyplot as plt
# 设置中文字体为黑体
plt.rcParams['font.sans-serif'] = ['SimHei']
# 解决负号显示问题
plt.rcParams['axes.unicode_minus'] = False
def GaussianNoise(image, mean, var):
    """
    为输入图像添加高斯噪声
    参数:
        image: 输入图像（需为numpy数组，值域[0,1]）
        mean: 噪声均值
        var: 噪声方差
    返回:
        noisy: 添加噪声后的图像（值域[0,1]）
    """
    row, col = image.shape
    sigma = var ** 0.5  # 计算标准差
    gauss = np.random.normal(mean, sigma, (row, col))  # 生成高斯噪声矩阵
    noisy = image + gauss  # 将噪声添加到原始图像
    noisy = np.clip(noisy, 0, 1)  # 确保像素值在[0,1]范围内
    return noisy


# 读取图像并归一化到[0,1]范围
img = cv2.imread('D:\\MyDIP\\001.bmp', 0)
img = img / 255.0

# 添加高斯噪声（均值0.1，方差0.05）
img_n = GaussianNoise(img, 0.1, 0.05)

# 计算噪声差异矩阵
K = img_n - img

# 创建子图显示结果
plt.subplot(131)
plt.imshow(img_n, 'gray')
plt.title('有噪图像')

plt.subplot(132)
plt.imshow(img, 'gray')
plt.title('原始图像')

plt.subplot(133)
plt.imshow(K, 'gray')
plt.title('提取的噪声')

# 显示所有子图
plt.show()

运行结果：

3.乘法运算

乘法运算能够实现灰度值的改变,达到修改图像亮度的目的。乘法也可以用来获得掩模图像,将所需要留下的区域设置为1,将不需要保留的区域设置为0,这样就能够通过乘法运算获取图像的目标区域。同时,乘法运算也经常用来实现卷积或相关处理。

运行代码如下：

# 导入库 
import numpy as np
import cv2
import matplotlib.pyplot as plt
# 设置中文字体为黑体
plt.rcParams['font.sans-serif'] = ['SimHei']
# 解决负号显示问题
plt.rcParams['axes.unicode_minus'] = False

# 读取灰度图像
img = cv2.imread('D:\\MyDIP\\001.bmp', 0)

# 使用OpenCV的multiply函数进行亮度调整
img1 = cv2.multiply(1.2, img)  # 将图像亮度增加20%
img2 = cv2.multiply(2, img)  # 将图像亮度加倍

# 创建子图显示原始图像和亮度调整后的图像
plt.subplot(131)
plt.imshow(img, 'gray')
plt.title('原始图像')

plt.subplot(132)
plt.imshow(img1, 'gray')
plt.title('乘以1.2')

plt.subplot(133)
plt.imshow(img2, 'gray')
plt.title('乘以2')

# 显示所有子图
plt.show()

运行结果：

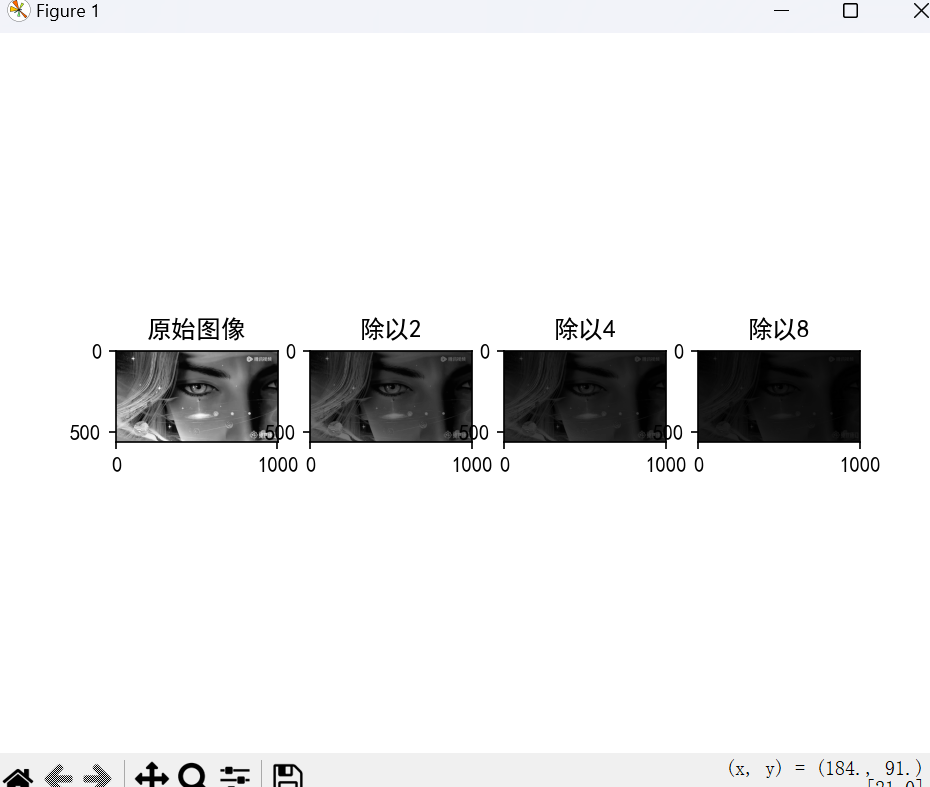
4.除法运算

除法运算可以改变像素的灰度值,调整图像亮度。也能够用来校正成像设备的非线性影响,常在 CT等医学图像中用到。

运行代码如下：

# 导入必要的库
import numpy as np
import cv2
import matplotlib.pyplot as plt
# 设置中文字体为黑体
plt.rcParams['font.sans-serif'] = ['SimHei']
# 解决负号显示问题
plt.rcParams['axes.unicode_minus'] = False

# 读取灰度图像
img = cv2.imread('D:\\MyDIP\\001.bmp', 0)

# 使用OpenCV的divide函数进行亮度降低
img1 = cv2.divide(img, 2)  # 将图像亮度降低为原来的1/2
img2 = cv2.divide(img, 4)  # 将图像亮度降低为原来的1/4
img3 = cv2.divide(img, 8)  # 将图像亮度降低为原来的1/8

# 创建子图显示原始图像和亮度降低后的图像
# vmin和vmax参数用于固定显示范围，确保不同图像使用相同的亮度标尺
plt.subplot(141)
plt.imshow(img, 'gray', vmin=0, vmax=255)
plt.title('原始图像')

plt.subplot(142)
plt.imshow(img1, 'gray', vmin=0, vmax=255)
plt.title('除以2')

plt.subplot(143)
plt.imshow(img2, 'gray', vmin=0, vmax=255)
plt.title('除以4')

plt.subplot(144)
plt.imshow(img3, 'gray', vmin=0, vmax=255)
plt.title('除以8')

# 显示所有子图
plt.show()

运行结果：

三、图像灰度直方图的显示

灰度直方图是图像灰度级分布的函数，是对灰度分布的统计。灰度直方点按照其灰度级的大小，统计每个值出现的频率，可以用公式表示p(k)= $\: \! n$ k/ $\, n$

其中,n是像素点的个数,ne是k级像素点的个数，且满足:

L-1

$\sum p(k)=1$ 。

K=0

灰度直方图仅仅反映了图像灰度级出现频率的分布,但是不能反映出具体位置的分布，即不能由灰度直方图确定图像,所以存在不同的图像可能有同样的灰度直方图，但是一幅图像只能存在一个灰度直方图。同时，图像若分割成子图，则所有子图的直方图加起来就是原图像的直方图。

运行代码如下：

# 导入库
import cv2
import matplotlib.pyplot as plt
# 设置中文字体为黑体
plt.rcParams['font.sans-serif'] = ['SimHei']
# 解决负号显示问题
plt.rcParams['axes.unicode_minus'] = False

# 读取灰度图像
img = cv2.imread('D:\\MyDIP\\001.bmp', 0)

# 创建子图显示原始图像
plt.subplot(131)
plt.imshow(img, 'gray')
plt.title('原始图像')

# 使用OpenCV的calcHist函数计算图像直方图
plt.subplot(132)
hist = cv2.calcHist([img], [0], None, [256], [0, 255])
plt.plot(hist)
plt.title('灰度直方图1')

# 使用Matplotlib的hist函数计算并绘制图像直方图
plt.subplot(133)
plt.hist(img.ravel(), 256, [0, 256])
plt.title('灰度直方图2')

# 显示所有子图
plt.show()

运行结果：

结果如图所示。图中分别用OpenCV和Matplotlib两个常用库获取图像的灰度直方图，可以看出两种方法画出的直方图一致。

四、图像变换

图像变换是将图像从空间域变换到频率域，然后在频率域对图像进行处理，实现一些空间域内无法实现的操作。常见图像变换包括离散傅里叶变换和离散余弦变换等等。

1.离散傅里叶变换

图像通过离散傅里叶变换,由空间域变换到频域,能量进行重新分布,可以通过对频域的数据进行处理,达到处理数字图像的目的。

运行代码如下：

# 导入必要的库
import cv2
import numpy as np
import matplotlib.pyplot as plt

# 设置Matplotlib显示中文字体为黑体
plt.rcParams['font.sans-serif'] = ['SimHei']
# 解决Matplotlib负号显示问题
plt.rcParams['axes.unicode_minus'] = False

# 读取灰度图像
img = cv2.imread('D:\\MyDIP\\001.bmp', 0)

# 进行离散傅里叶变换（DFT）
img_dft = cv2.dft(img / 255, flags=cv2.DFT_COMPLEX_OUTPUT)

# 将频谱中心化
img_cen = np.fft.fftshift(img_dft)

# 进行逆离散傅里叶变换（IDFT）
img_s = cv2.idft(img_dft)

# 计算各步骤的幅度谱
img_dft = cv2.magnitude(img_dft[:, :, 0], img_dft[:, :, 1])
img_cen = cv2.magnitude(img_cen[:, :, 0], img_cen[:, :, 1])
img_s = cv2.magnitude(img_s[:, :, 0], img_s[:, :, 1])

# 创建子图显示结果
plt.subplot(141)
plt.imshow(img, 'gray')
plt.title('原始图像')

plt.subplot(142)
plt.imshow(20 * np.log(img_dft), 'gray')
plt.title('DFT变换后频谱')

plt.subplot(143)
plt.imshow(20 * np.log(img_cen), 'gray')
plt.title('中心化频谱')

plt.subplot(144)
plt.imshow(img_s, 'gray')
plt.title('IDFT重建图像')

# 显示所有子图
plt.show()

运行结果：

2.离散余弦变换

离散余弦变化是一种特殊的离散傅里叶变换。当函数为实偶函数时，傅里叶变换展开式只存在余弦项，故称为离散余弦变换。
使用OpenCV进行图像的离散余弦变换（DCT）及其逆变换。

运行代码如下：

# 导入必要的库
import cv2
import numpy as np
import matplotlib.pyplot as plt

# 设置Matplotlib显示中文字体为黑体
plt.rcParams['font.sans-serif'] = ['SimHei']
# 解决Matplotlib负号显示问题
plt.rcParams['axes.unicode_minus'] = False

# 读取灰度图像
img = cv2.imread('D:\\MyDIP\\001.bmp', 0)

# 进行离散余弦变换（DCT）
img_dft = cv2.dct(img / 255)

# 进行逆离散余弦变换（IDCT）
img_s = cv2.idct(img_dft)

# 创建子图显示结果
plt.subplot(131)
plt.imshow(img, 'gray')
plt.title('原始图像')

plt.subplot(132)
# 使用对数变换增强DCT系数的显示效果，并取绝对值避免负值影响
plt.imshow(20 * np.log(abs(img_dft)), 'gray')
plt.title('DCT变换后频谱')

plt.subplot(133)
plt.imshow(img_s, 'gray')
plt.title('IDCT重建图像')

# 显示所有子图
plt.show()

运行结果：

五、直方图均衡化

直方图增强主要针对图像像素值过于集中，导致图像对比度降低，因此实验时先对图像进行灰度值压缩，再用直方图均衡化的方法来实现图像增强。
映射方法公式：
在这里插入图片描述
注：n是图像中像素的总和
是当前灰度级的像素个数
L是图像中可能的灰度级总数

运行代码如下：

# 导入必要的库
import cv2
import matplotlib.pyplot as plt

# 设置Matplotlib显示中文字体为黑体
plt.rcParams['font.sans-serif'] = ['SimHei']
# 解决Matplotlib负号显示问题
plt.rcParams['axes.unicode_minus'] = False

# 读取灰度图像
img = cv2.imread('D:\\MyDIP\\001.bmp', 0)

# 调整图像亮度：增加亮度
img_h = cv2.add(img, 150)

# 调整图像亮度：降低亮度
img_l = cv2.multiply(img, 0.2)

# 计算调整亮度后的直方图
img_h_t = cv2.calcHist([img_h], [0], None, [256], [0, 256])
img_l_t = cv2.calcHist([img_l], [0], None, [256], [0, 256])

# 对调整亮度后的图像进行直方图均衡化
img_h_h = cv2.equalizeHist(img_h)
img_l_h = cv2.equalizeHist(img_l)

# 计算均衡化后的直方图
img_h_l = cv2.calcHist([img_h_h], [0], None, [256], [0, 256])
img_l_l = cv2.calcHist([img_l_h], [0], None, [256], [0, 256])

# 创建子图显示结果
plt.subplot(241)
plt.imshow(img_h, 'gray')
plt.title('亮度增加图像')

plt.subplot(242)
plt.imshow(img_h_h, 'gray')
plt.title('亮度增加图像均衡化')

plt.subplot(245)
plt.plot(img_h_t, 'gray')
plt.title('亮度增加图像直方图')

plt.subplot(246)
plt.plot(img_h_l, 'gray')
plt.title('亮度增加图像均衡化直方图')

plt.subplot(243)
plt.imshow(img_l, 'gray')
plt.title('亮度降低图像')

plt.subplot(244)
plt.imshow(img_l_h, 'gray')
plt.title('亮度降低图像均衡化')

plt.subplot(247)
plt.plot(img_l_t, 'gray')
plt.title('亮度降低图像直方图')

plt.subplot(248)
plt.plot(img_l_l, 'gray')
plt.title('亮度降低图像均衡化直方图')

# 显示所有子图
plt.show()

运行结果：