初学python的我开始Leetcode题8-3

最新推荐文章于 2025-05-03 16:27:41 发布

电院大学僧

最新推荐文章于 2025-05-03 16:27:41 发布

阅读量847

点赞数 13

文章标签： leetcode 算法 python

本文链接：https://blog.csdn.net/2301_79903353/article/details/147655621

版权

提示：100道LeetCode热题-8-3主要是二叉树相关，包括三题：将有序数组转换为二叉搜索树、验证二叉搜索树、二叉搜索树中第K小的元素。由于初学，所以我的代码部分仅供参考。

前言

五一快乐~

二叉搜索树奉上~

提示：以下是本篇文章正文内容，下面结果代码仅供参考

题目1：将有序数组转换为二叉搜索树

1.题目要求：

题目如下：

给你一个整数数组 nums ，其中元素已经按升序排列，请你将其转换为一棵平衡二叉搜索树。

示例 1：
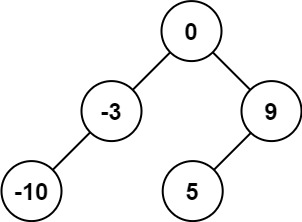
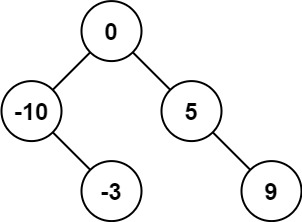
输入：nums = [-10,-3,0,5,9]
输出：[0,-3,9,-10,null,5]
解释：[0,-10,5,null,-3,null,9] 也将被视为正确答案：
示例 2：
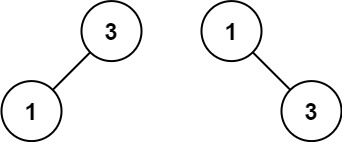
输入：nums = [1,3]
输出：[3,1]
解释：[1,null,3] 和 [3,1] 都是高度平衡二叉搜索树。
提示：

1 <= nums.length <=
- <= nums[i] <=
nums 按 严格递增 顺序排列

代码框架已经提供如下：

# Definition for a binary tree node.

# class TreeNode(object):

# def __init__(self, val=0, left=None, right=None):

# self.val = val

# self.left = left

# self.right = right

class Solution(object):

def sortedArrayToBST(self, nums):

"""

:type nums: List[int]

:rtype: Optional[TreeNode]

"""

2.结果代码：

class Solution(object):
    def sortedArrayToBST(self, nums):
        if not nums:
            return
        mid_index = len(nums) // 2
        return TreeNode(nums[mid_index], self.sortedArrayToBST(nums[:mid_index]), self.sortedArrayToBST(nums[mid_index + 1:]))

说明：

1）更快，Python 的列表切片操作在底层是高度优化的，对于小数组，切片操作的常数开销可能比递归调用的开销小。

2）小心Python 的递归深度默认为 1000。如果数组非常大，递归调用可能会导致栈溢出。。

题目2：验证二叉搜索树

1.题目要求：

题目如下：

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效二叉搜索树定义如下：

节点的左子树只包含小于当前节点的数。
节点的右子树只包含大于当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。

示例 1：
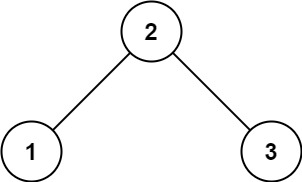
输入：root = [2,1,3]
输出：true
示例 2：
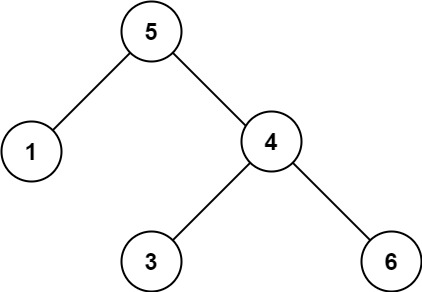
输入：root = [5,1,4,null,null,3,6]
输出：false
解释：根节点的值是 5 ，但是右子节点的值是 4 。
提示：

树中节点数目范围在[1, ] 内
- <= Node.val <= - 1

代码框架已经提供如下：

# Definition for a binary tree node.

# class TreeNode(object):

# def __init__(self, val=0, left=None, right=None):

# self.val = val

# self.left = left

# self.right = right

class Solution(object):

def isValidBST(self, root):

"""

:type root: Optional[TreeNode]

:rtype: bool

"""

2.结果代码：

方法一：递归检查（带范围）

# Definition for a binary tree node.
class TreeNode(object):
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

class Solution(object):
    def isValidBST(self, root):
        """
        :type root: TreeNode
        :rtype: bool
        """
        def is_valid_bst_helper(node, lower=float('-inf'), upper=float('inf')):
            if not node:
                return True
            if node.val <= lower or node.val >= upper:
                return False
            return (is_valid_bst_helper(node.left, lower, node.val) and
                    is_valid_bst_helper(node.right, node.val, upper))

        return is_valid_bst_helper(root)

定义了一个递归辅助函数 is_valid_bst_helper，它接收三个参数。
如果当前节点为空（node 为 None），返回 True，因为空树是有效的二叉搜索树。
如果当前节点的值小于等于下界或大于等于上界，返回 False，因为这违反了二叉搜索树的性质。
递归检查左右子树：
- 对左子树递归调用时，更新上界为当前节点的值（node.val），因为左子树的所有值必须小于当前节点的值。
- 对右子树递归调用时，更新下界为当前节点的值，因为右子树的所有值必须大于当前节点的值。
- 递归检查左右子树是否都满足二叉搜索树的性质。

方法二：中序遍历

# Definition for a binary tree node.
class TreeNode(object):
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

class Solution(object):
    def isValidBST(self, root):
        """
        :type root: TreeNode
        :rtype: bool
        """
        stack = []
        prev_val = float('-inf')
        curr = root

        while curr or stack:
            while curr:
                stack.append(curr)
                curr = curr.left

            curr = stack.pop()
            if curr.val <= prev_val:
                return False
            prev_val = curr.val
            curr = curr.right

        return True

使用一个栈来模拟递归的调用过程，初始化一个指针 curr 指向根节点，prev_val 用于记录上一个访问的节点值（初始为负无穷）。
遍历过程：
- 沿着左子树一直向下，将节点压入栈中，直到左子树为空。
- 弹出栈顶节点（即当前子树的根节点），检查其值是否大于 prev_val。
- 如果当前节点的值小于等于 prev_val，返回 False，因为这违反了二叉搜索树的性质。
- 更新 prev_val 为当前节点的值，然后将指针移动到右子树。

题目3：二叉搜索树中第K小的元素

1.题目要求：

题目如下：

给定一个二叉搜索树的根节点 root ，和一个整数 k ，请你设计一个算法查找其中第 k 小的元素（从 1 开始计数）。

示例 1：
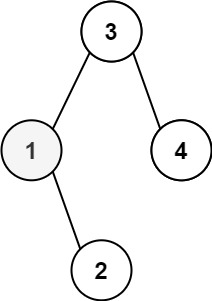
输入：root = [3,1,4,null,2], k = 1
输出：1
示例 2：
输入：root = [5,3,6,2,4,null,null,1], k = 3
输出：3
提示：

树中的节点数为 n 。
1 <= k <= n <=
0 <= Node.val <=

进阶：如果二叉搜索树经常被修改（插入/删除操作）并且你需要频繁地查找第 k 小的值，你将如何优化算法？

代码框架已经提供如下：

# Definition for a binary tree node.

# class TreeNode(object):

# def __init__(self, val=0, left=None, right=None):

# self.val = val

# self.left = left

# self.right = right

class Solution(object):

def kthSmallest(self, root, k):

"""

:type root: Optional[TreeNode]

:type k: int

:rtype: int

"""

2.结果代码：

class Solution:
    def kthSmallest(self, root, k):
        stack = []
        curr = root
        count = 0

        while curr or stack:
            while curr:
                stack.append(curr)
                curr = curr.left
            curr = stack.pop()
            count += 1
            if count == k:
                return curr.val
            curr = curr.right

说明：使用栈模拟递归过程，避免递归调用的开销。

逻辑：