AVL树详解及代码实现

什么是二叉搜索树？

首先回顾之前学习的二叉搜索树，二叉搜索树又叫二叉排序树，它或者是一颗空树，或者是具有以下性质的二叉树：

若它的左子树不为空，则左子树所有节点都小于根节点的值

若它的右子树不为空，则右子树所有节点都大于根节点的值

它的左右子树也分别为二叉搜索树

总结二叉搜索树具有以下性质：

1.二叉搜索树中最左侧的节点是树中最小的节点，最右侧节点一定是树中最大的节点。

2.采用中序遍历遍历二叉搜索树，是一个有序的序列。

对于二叉树的查找，平均情况下时间复杂度是O(logN)

但是对于单分支的树，时间复杂度就是O(N)

所以对于单分支的树，二叉树就不能够快速搜索了，所以为了解决二叉搜索树不平衡的问题，引入了AVL树，AVL接近与平衡二叉树。

什么是AVL树

一颗AVL树或者是空树，或者是具有以下性质的二叉搜索树：

1.它的左右子树都是AVL树

2.左右子树高度之差（简称平衡因子）的绝对值不超过1（-1/0/1）

AVL树的高度可以保持在O(logN)，搜索时间复杂度O(logN)

代码实现

节点结构与根节点定义

public class AVLTree {

    static class TreeNode {
        public int val; //节点值
        public int bf; //平衡因子
        public TreeNode left; //左子树
        public TreeNode right; //右子树
        public TreeNode parent; //父节点
        public TreeNode(int val) {
            this.val = val;
        }
    }

    public  TreeNode root;
}

新增节点

public boolean insert(int val) {
        TreeNode node = new TreeNode(val);
        if(root == null) {
            root = node;
            return true;
        }
        TreeNode parent = null;
        TreeNode cur = root;
        while (cur != null) {  //插入节点
            if(cur.val < val) {
                parent = cur;
                cur = cur.right;
            } else if(cur.val > val) {
                parent = cur;
                cur = cur.left;
            } else {
                return false;
            }
        }
        if(parent.val > val) {
            parent.left = node;
        } else {
            parent.right = node;
        }
        node.parent = parent;
        cur = node;
        while (parent != null) {  //调整平衡因子
            if(parent.right == cur) {
                parent.bf++;
            } else {
                parent.bf--;
            }
            if(parent.bf == 0) {
                break;
            } else if(parent.bf == 1 || parent.bf == -1) {
                //需要继续往上调整
                cur = parent;
                parent = parent.parent;
            } else {
                //需要旋转达到平衡的效果
                if(parent.bf == 2) {
                    if(cur.bf == 1) {
                        rotateLeft(parent);
                    } else {
                        //cur.bf = -1
                        rotateRL(parent);
                    }
                } else {
                    //parent.bf=-2
                    if(cur.bf == 1) {
                        rotateLR(parent);
                    } else { //右单旋
                        //cur.bf = -1
                        rotateRight(parent);
                    }
                }
                //已经平衡了，可以退出循环
                break;
            }
        }
        return true;
    }

右单旋

左边高度高，向右旋转

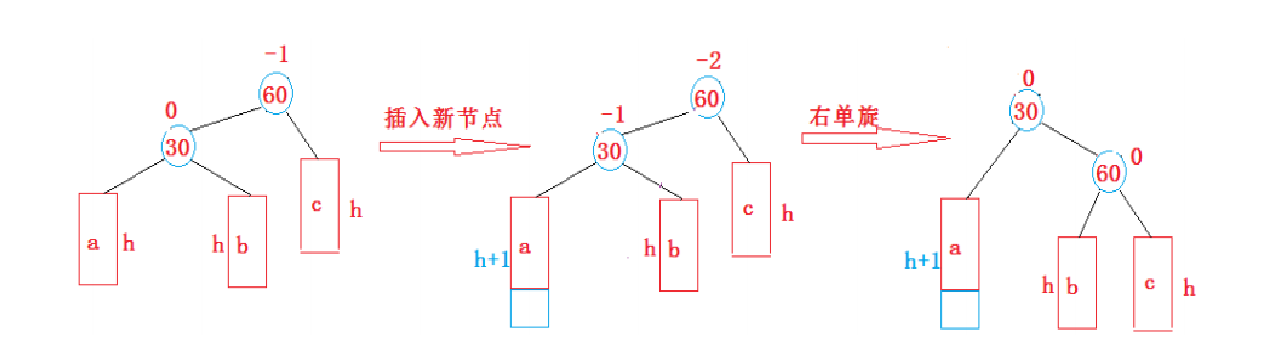
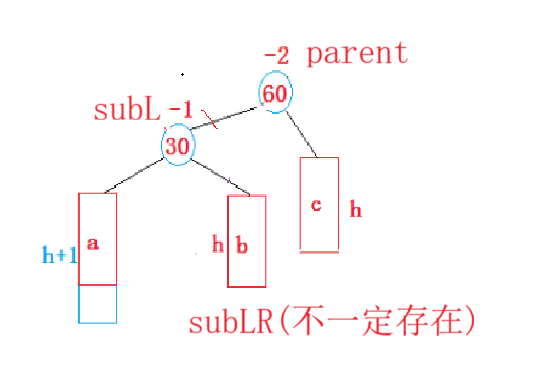
右单旋就是将左边提起，把subLR连到parent的左边，parent连到subL的右边，就跟将subL提起来了一样。

private void rotateRight(TreeNode parent) {
        TreeNode subL = parent.left; //记录左子树
        TreeNode subLR = subL.right; //记录左子树的右子树

        parent.left = subLR;  //修改父亲节点左边
        subL.right = parent;  //修改左子树的右边为父亲节点
        if(subLR != null) {  //修改sbuLR的父亲指向
            subLR.parent = parent;
        }
        //在修改parent节点的parent节点指向之前必须先记录下来
        TreeNode pParent = parent.parent;
        //修改parent的父亲
        parent.parent = subL;
        //必须要判断parent是不是主节点，如果是，root的值要进行修改
        if(parent == root) {
            root = subL;
            root.parent = null;
        } else {
            //修改subL的父亲
            subL.parent = pParent;
            //修改parent父亲的指向
            if(pParent.left == parent) {
                pParent.left = subL;
            } else {
                pParent.right = subL;
            }
        }
        //修改平衡因子
        subL.bf = 0;
        parent.bf = 0;
    }

左单旋

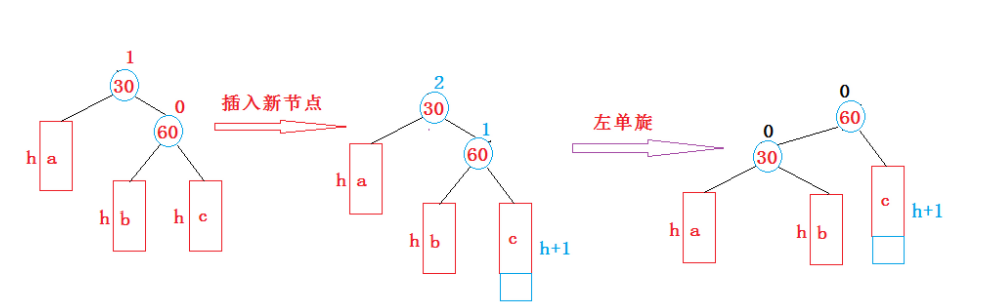
左单旋和右单旋是相同的原理

private void rotateLeft(TreeNode parent) {
        TreeNode subR = parent.right;
        TreeNode subRL = subR.left;

        //修改左右指向
        parent.right = subRL;
        subR.left = parent;

        //修改父亲节点指向
        if(subRL != null) {
            subRL.parent = parent;
        }
        TreeNode pParent = parent.parent;
        parent.parent = subR;
        //修改parent的父亲指向
        if(parent == root) {
            root = subR;
            root.parent = null;
        } else {
            if(pParent.left == parent) {
                pParent.left = subR;
            } else {
                pParent.right = subR;
            }
            subR.parent = pParent;
        }
        //修改平衡因子
        parent.bf = 0;
        subR.bf = 0;
    }

左右双旋

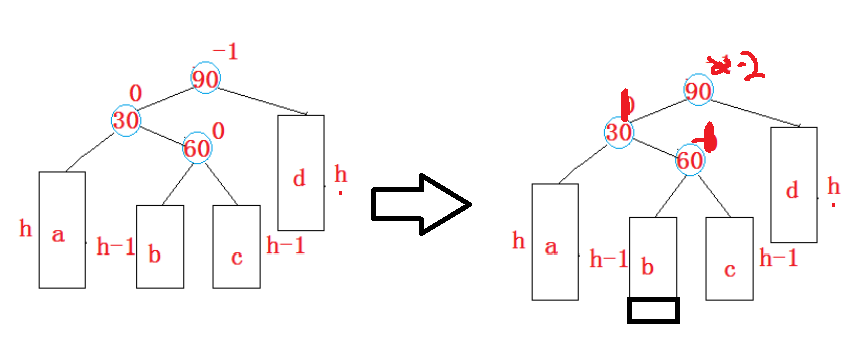
此时，只进行右旋很明显还是不能平衡，因为60的那个子树比较高，连在90的左边依旧比较高，所以先将30作为parent进行一次左旋，降低右边的高度，然后再对90进行右旋

先左旋

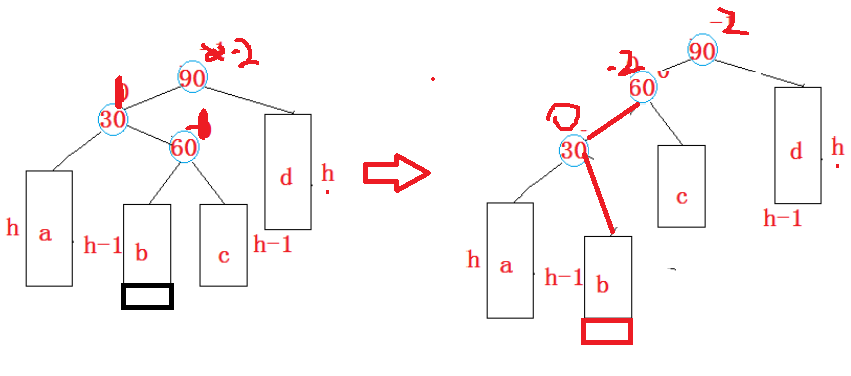
再右旋

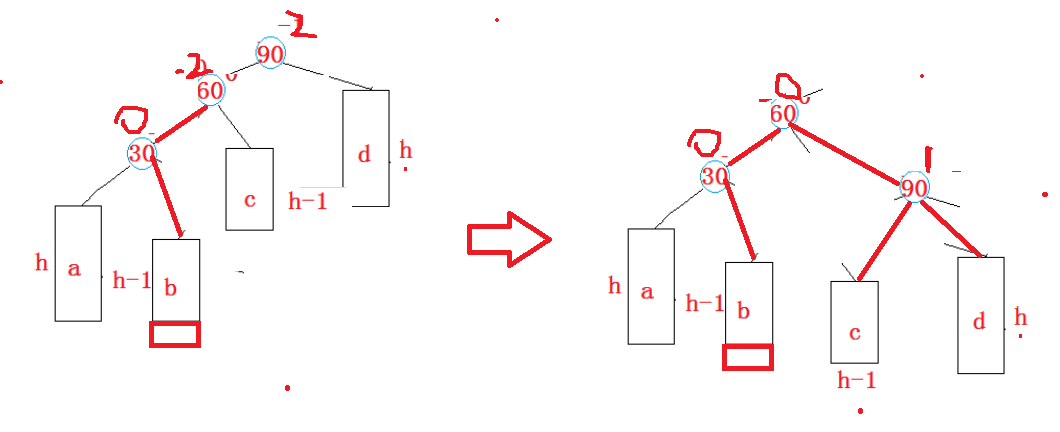上图是新增节点在b的情况，如果新增节点是在c上面的时候

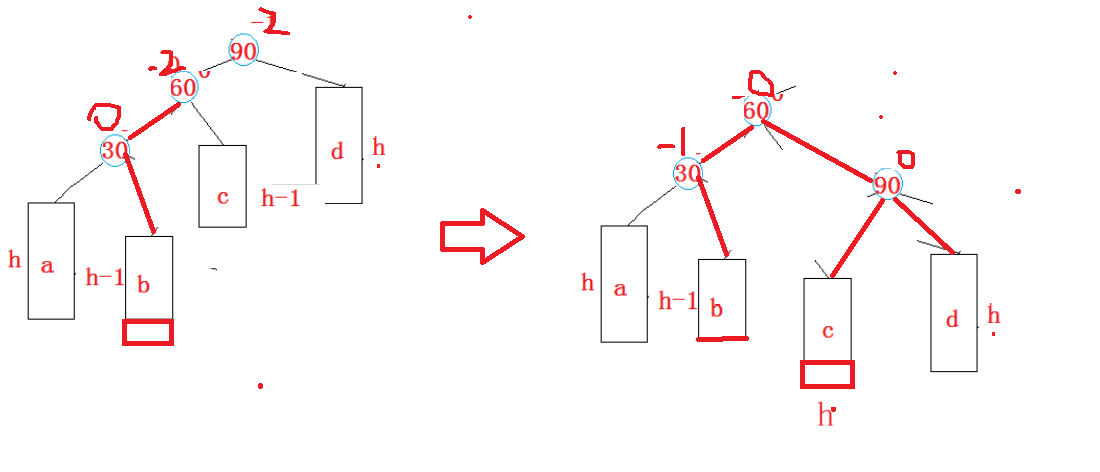
两种情况下旋转的方式一样，但是平衡因子却不一样

如果b本身就是新增的节点，如下图，bf=0

此时平衡因子都为0，但是在左旋和右旋的时候平衡因子已经进行修改了，所以这里可以不单独进行修改

private void rotateLR(TreeNode parent) {
        TreeNode subL = parent.left;
        TreeNode subLR = subL.right;
        int bf = subLR.bf;
        rotateLeft(subL);
        rotateRight(parent);
        if(bf == -1) {
            subL.bf = 0;
            subLR.bf = 0;
            parent.bf = 1;
        } else {
            subL.bf = -1;
            subLR.bf = 0;
            parent.bf = 0;
        }

    }

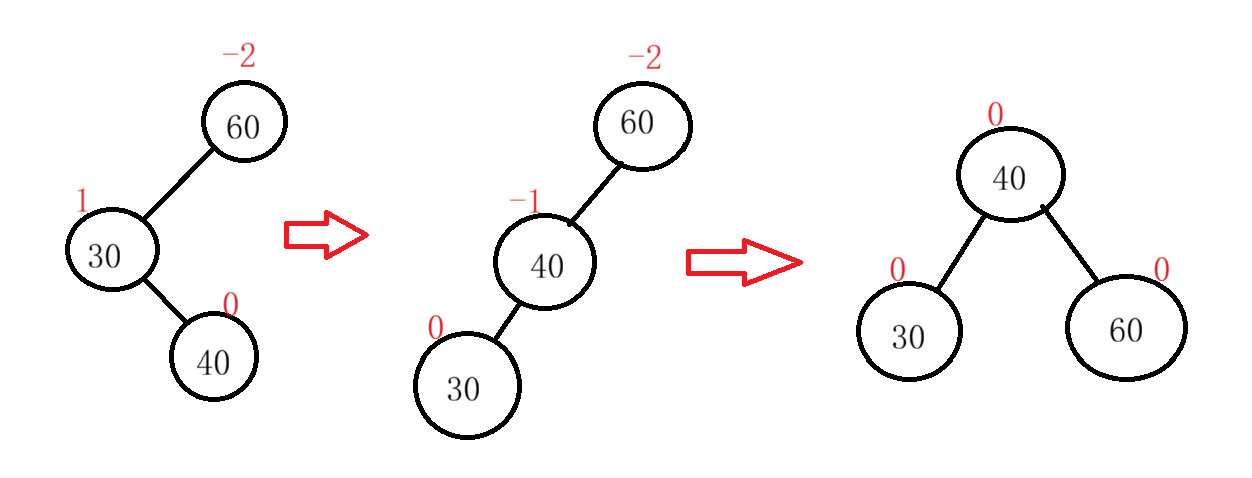
右左双旋

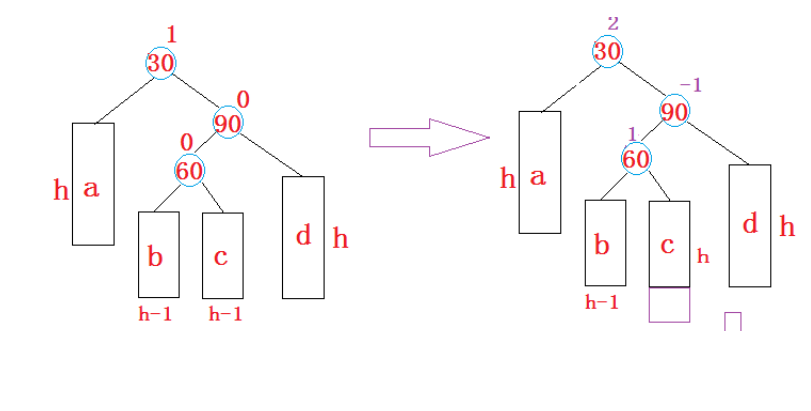
跟左右旋类似，先右旋

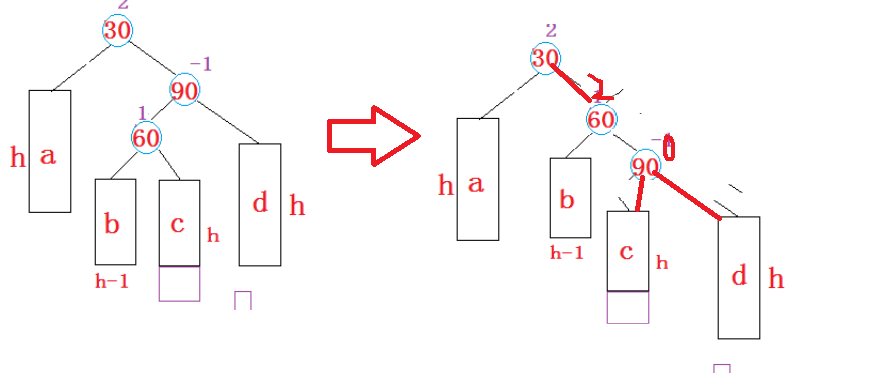
再左旋

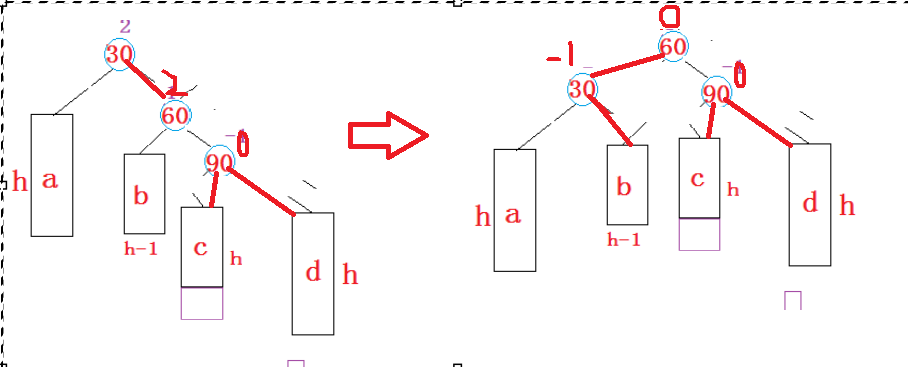
如果新增节点在b上的话，旋转方式一样，但是平衡因子不一样

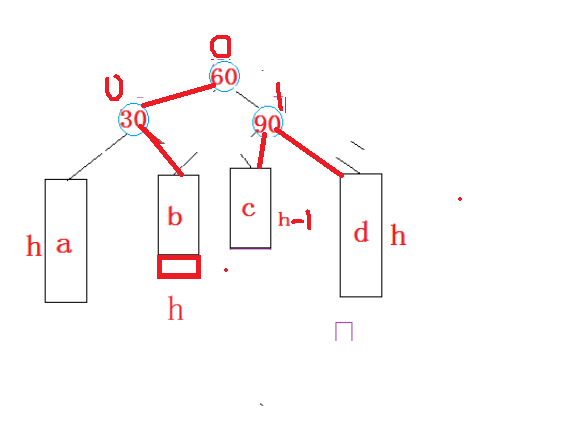
这里也有bf=0的情况，同左右双旋，平衡因子都为0，不需要额外进行修改。

代码实现：

private void rotateRL(TreeNode parent) {
        TreeNode subR = parent.right;
        TreeNode subRL = subR.left;
        int bf = subRL.bf;
        rotateRight(parent.right);
        rotateLeft(parent);
        if(bf == 1) {
            parent.bf = -1;
            subR.bf = 0;
            subRL.bf = 0;
        }else if(bf == -1){
            parent.bf = 0;
            subR.bf = 1;
            subRL.bf = 0;
        }
    }

验证是否为AVL树

//1.中序遍历必须有序
    public void inOrder(TreeNode root) {
        if(root == null) {
            return;
        }
        inOrder(root.left);
        System.out.print(root.val+" ");
        inOrder(root.right);
    }
    //2.左右子树高度不超过1，并且平衡因子与左右差相等
    public int height(TreeNode root) {
        if(root == null) {
            return 0;
        }
        return Math.max(height(root.left),height(root.right)) + 1;
    }
    public boolean isBalanced(TreeNode root) {
        if(root == null) {
            return true;
        }
        int leftH = height(root.left);
        int rightH = height(root.right);
        if(rightH - leftH != root.bf) {
            System.out.println("这个节点:" + root.val + "平衡因子异常");
        }
        return Math.abs(rightH-leftH) <= 1 && isBalanced(root.left) && isBalanced(root.right);
    }

测试：

public class Test {
    public static void main(String[] args) {
        AVLTree avlTree = new AVLTree();
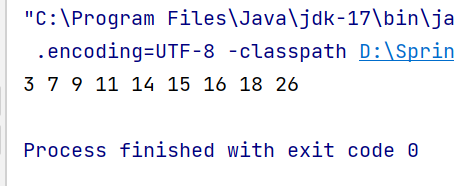
        int[] array = new int[]{16, 3, 7, 11, 9, 26, 18, 14, 15};
        for (int i = 0; i < array.length; i++) {
            avlTree.insert(array[i]);
        }
        avlTree.inOrder(avlTree.root);
        System.out.println();
        avlTree.isBalanced(avlTree.root);
    }
}

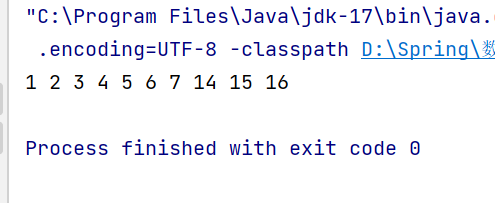
public class Test {
    public static void main(String[] args) {
        AVLTree avlTree = new AVLTree();
        int[] array = new int[]{4, 2, 6, 1, 3, 5, 15, 7, 16, 14};
        for (int i = 0; i < array.length; i++) {
            avlTree.insert(array[i]);
        }
        avlTree.inOrder(avlTree.root);
        System.out.println();
        avlTree.isBalanced(avlTree.root);
    }
}

完整全部代码

public class AVLTree {

    static class TreeNode {
        public int val; //节点值
        public int bf; //平衡因子
        public TreeNode left; //左子树
        public TreeNode right; //右子树
        public TreeNode parent; //父节点
        public TreeNode(int val) {
            this.val = val;
        }
    }

    public  TreeNode root;

    public boolean insert(int val) {
        TreeNode node = new TreeNode(val);
        if(root == null) {
            root = node;
            return true;
        }
        TreeNode parent = null;
        TreeNode cur = root;
        while (cur != null) {  //插入节点
            if(cur.val < val) {
                parent = cur;
                cur = cur.right;
            } else if(cur.val > val) {
                parent = cur;
                cur = cur.left;
            } else {
                return false;
            }
        }
        if(parent.val > val) {
            parent.left = node;
        } else {
            parent.right = node;
        }
        node.parent = parent;
        cur = node;
        while (parent != null) {  //调整平衡因子
            if(parent.right == cur) {
                parent.bf++;
            } else {
                parent.bf--;
            }
            if(parent.bf == 0) {
                break;
            } else if(parent.bf == 1 || parent.bf == -1) {
                //需要继续往上调整
                cur = parent;
                parent = parent.parent;
            } else {
                //需要旋转达到平衡的效果
                if(parent.bf == 2) {
                    if(cur.bf == 1) {
                        rotateLeft(parent);
                    } else {
                        //cur.bf = -1
                        rotateRL(parent);
                    }
                } else {
                    //parent.bf=-2
                    if(cur.bf == 1) {
                        rotateLR(parent);
                    } else { //右单旋
                        //cur.bf = -1
                        rotateRight(parent);
                    }
                }
                //已经平衡了，可以退出循环
                break;
            }
        }
        return true;
    }

    private void rotateRL(TreeNode parent) {
        TreeNode subR = parent.right;
        TreeNode subRL = subR.left;
        int bf = subRL.bf;
        rotateRight(subR);
        rotateLeft(parent);
        if(bf == 1) {
            parent.bf = -1;
            subRL.bf = subR.bf = 0;
        } else if(bf == -1){
            parent.bf = subRL.bf = 0;
            subR.bf = 1;
        }
    }

    private void rotateLR(TreeNode parent) {
        TreeNode subL = parent.left;
        TreeNode subLR = subL.right;
        int bf = subLR.bf;
        rotateLeft(subL);
        rotateRight(parent);
        if(bf == -1) {
            subL.bf = 0;
            subLR.bf = 0;
            parent.bf = 1;
        } else if(bf == 1){
            subL.bf = -1;
            subLR.bf = 0;
            parent.bf = 0;
        }

    }

    private void rotateLeft(TreeNode parent) {
        TreeNode subR = parent.right;
        TreeNode subRL = subR.left;

        //修改左右指向
        parent.right = subRL;
        subR.left = parent;

        //修改父亲节点指向
        if(subRL != null) {
            subRL.parent = parent;
        }
        TreeNode pParent = parent.parent;
        parent.parent = subR;
        //修改parent的父亲指向
        if(parent == root) {
            root = subR;
            root.parent = null;
        } else {
            if(pParent.left == parent) {
                pParent.left = subR;
            } else {
                pParent.right = subR;
            }
            subR.parent = pParent;
        }
        //修改平衡因子
        parent.bf = 0;
        subR.bf = 0;
    }

    private void rotateRight(TreeNode parent) {
        TreeNode subL = parent.left; //记录左子树
        TreeNode subLR = subL.right; //记录左子树的右子树

        parent.left = subLR;  //修改父亲节点左边
        subL.right = parent;  //修改左子树的右边为父亲节点
        if(subLR != null) {  //修改sbuLR的父亲指向
            subLR.parent = parent;
        }
        //在修改parent节点的parent节点指向之前必须先记录下来
        TreeNode pParent = parent.parent;
        //修改parent的父亲
        parent.parent = subL;
        //必须要判断parent是不是主节点，如果是，root的值要进行修改
        if(parent == root) {
            root = subL;
            root.parent = null;
        } else {
            //修改subL的父亲
            subL.parent = pParent;
            //修改parent父亲的指向
            if(pParent.left == parent) {
                pParent.left = subL;
            } else {
                pParent.right = subL;
            }
        }
        //修改平衡因子
        subL.bf = 0;
        parent.bf = 0;
    }

    //1.中序遍历必须有序
    public void inOrder(TreeNode root) {
        if(root == null) {
            return;
        }
        inOrder(root.left);
        System.out.print(root.val+" ");
        inOrder(root.right);
    }
    //2.左右子树高度不超过1，并且平衡因子与左右差相等
    public int height(TreeNode root) {
        if(root == null) {
            return 0;
        }
        return Math.max(height(root.left),height(root.right)) + 1;
    }
    public boolean isBalanced(TreeNode root) {
        if(root == null) {
            return true;
        }
        int leftH = height(root.left);
        int rightH = height(root.right);
        if(rightH - leftH != root.bf) {
            System.out.println("这个节点:" + root.val + "平衡因子异常");
        }
        return Math.abs(rightH-leftH) <= 1 && isBalanced(root.left) && isBalanced(root.right);
    }
}