代码随想录算法训练营第三十八天、三十九天|动态规划part11、12

原创于 2025-08-08 20:57:42 发布 · 937 阅读

10 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #动态规划 #leetcode #java #数据结构

动态规划专栏收录该内容

11 篇文章

订阅专栏

LeetCode 1143 最长公共子序列

题目链接：1143. 最长公共子序列 - 力扣（LeetCode）

给定两个字符串 text1 和 text2，返回这两个字符串的最长公共子序列的长度。如果不存在公共子序列，返回 0 。

一个字符串的子序列是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。

例如，"ace" 是 "abcde" 的子序列，但 "aec" 不是 "abcde" 的子序列。
两个字符串的公共子序列是这两个字符串所共同拥有的子序列。

示例 1：

输入：text1 = "abcde", text2 = "ace"
输出：3
解释：最长公共子序列是 "ace" ，它的长度为 3 。
示例 2：

输入：text1 = "abc", text2 = "abc"
输出：3
解释：最长公共子序列是 "abc" ，它的长度为 3 。
示例 3：

输入：text1 = "abc", text2 = "def"
输出：0
解释：两个字符串没有公共子序列，返回 0 。

1.确定dp数组以及下标的含义：

dp[i][j]表示text1前i个元素和text2前j个元素的最长公共子序列的长度。

2.递推公式：

如果text1[i-1]==text2[j-1]，dp[i][j]=dp[i-1][j-1]+1；

如果text1[i-1]!=text2[j-1]，有两种情况：

text1的前i个元素和text2的前j个元素的最长公共子序列的最后一个元素不等于text1[i-1]，说明这个最长公共子序列是text1的前i-1个元素和text2的前j个元素的最长公共子序列，所以dp[i][j]=dp[i-1][j]；

text1的前i个元素和text2的前j个元素的最长公共子序列的最后一个元素不等于text2[j-1]，说明这个最长公共子序列是text1的前i个元素和text2的前j-1个元素的最长公共子序列，所以dp[i][j]=dp[i][j-1]。

所以dp[i][j]=max(dp[i-1][j],dp[i][j-1])。

3.初始化：

初始化dp数组第一行第一列均为0即可，表示任何一个字符串为空时，最长公共子序列的长度肯定为0。

4.确定遍历顺序：

行优先从前向后遍历。

5.举例推导dp数组：

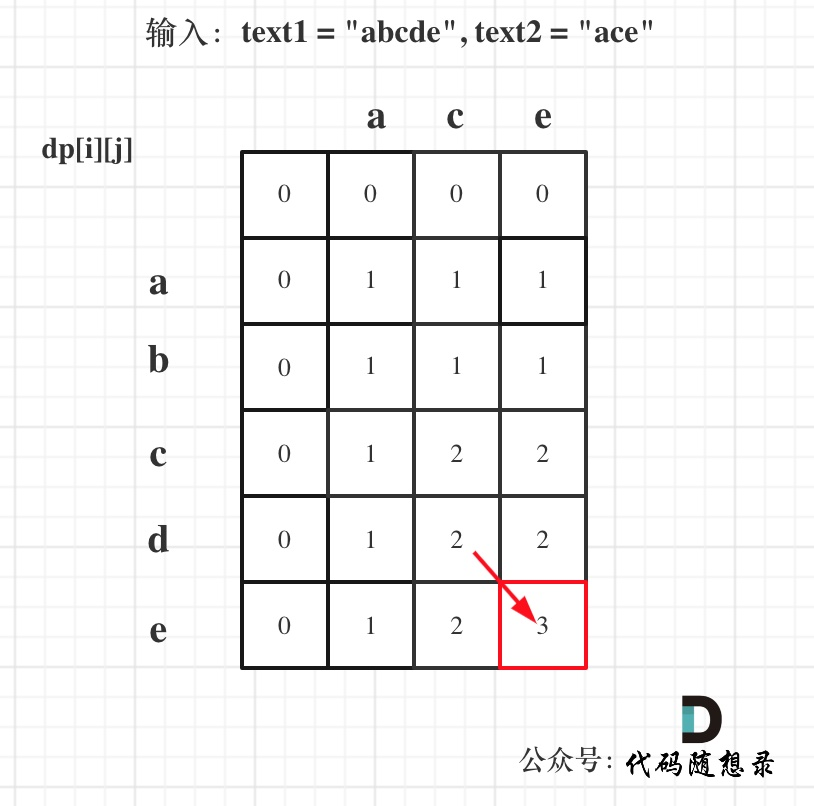
代码如下：

class Solution {
    public int longestCommonSubsequence(String text1, String text2) {
        int m=text1.length();
        int n=text2.length();
        int[][] dp=new int[m+1][n+1];
        for(int i=1;i<=m;i++){
            for(int j=1;j<=n;j++){
                if(text1.charAt(i-1)==text2.charAt(j-1))dp[i][j]=dp[i-1][j-1]+1;
                else dp[i][j]=Math.max(dp[i-1][j],dp[i][j-1]);
            }
        }
        return dp[m][n];
    }
}

LeetCode 1035 不相交的线

题目链接：1035. 不相交的线 - 力扣（LeetCode）

在两条独立的水平线上按给定的顺序写下 nums1 和 nums2 中的整数。

现在，可以绘制一些连接两个数字 nums1[i] 和 nums2[j] 的直线，这些直线需要同时满足：

nums1[i] == nums2[j]
且绘制的直线不与任何其他连线（非水平线）相交。
请注意，连线即使在端点也不能相交：每个数字只能属于一条连线。

以这种方法绘制线条，并返回可以绘制的最大连线数。

示例 1：

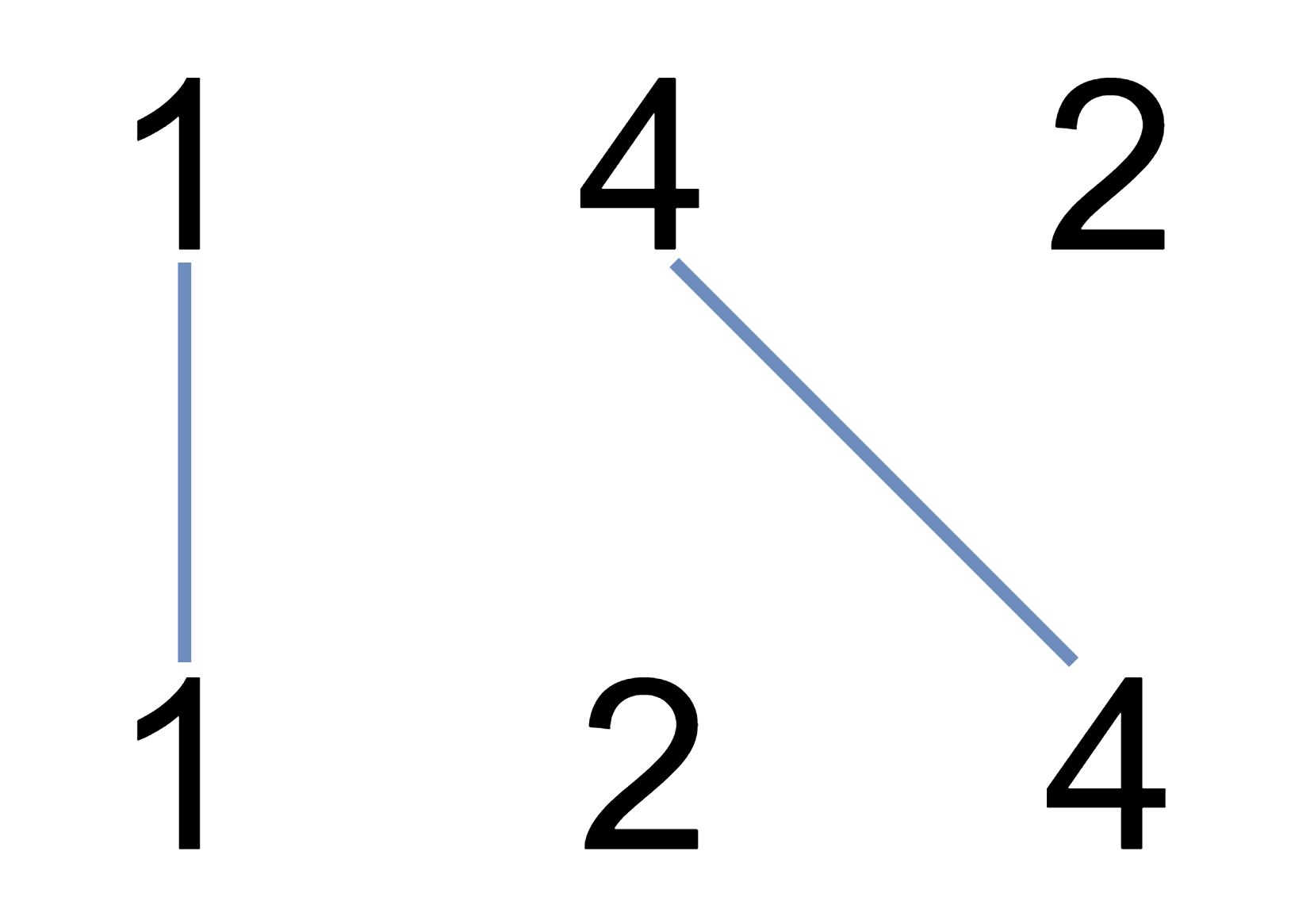
输入：nums1 = [1,4,2], nums2 = [1,2,4]
输出：2
解释：可以画出两条不交叉的线，如上图所示。
但无法画出第三条不相交的直线，因为从 nums1[1]=4 到 nums2[2]=4 的直线将与从 nums1[2]=2 到 nums2[1]=2 的直线相交。
示例 2：

输入：nums1 = [2,5,1,2,5], nums2 = [10,5,2,1,5,2]
输出：3
示例 3：

输入：nums1 = [1,3,7,1,7,5], nums2 = [1,9,2,5,1]
输出：2

这个题本质就是求两个数组的最大公共子序列，和上一题一样。

class Solution {
    public int maxUncrossedLines(int[] nums1, int[] nums2) {
        int m=nums1.length;
        int n=nums2.length;
        int[][] dp=new int[m+1][n+1];
        for(int i=1;i<=m;i++){
            for(int j=1;j<=n;j++){
                if(nums1[i-1]==nums2[j-1])dp[i][j]=dp[i-1][j-1]+1;
                else dp[i][j]=Math.max(dp[i-1][j],dp[i][j-1]);
            }
        }
        return dp[m][n];
    }
}

LeetCode 53 最大子数组和

题目链接：53. 最大子数组和 - 力扣（LeetCode）

给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

子数组是数组中的一个连续部分。

示例 1：

输入：nums = [-2,1,-3,4,-1,2,1,-5,4]
输出：6
解释：连续子数组 [4,-1,2,1] 的和最大，为 6 。
示例 2：

输入：nums = [1]
输出：1
示例 3：

输入：nums = [5,4,-1,7,8]
输出：23

1.确定dp数组以及下标含义：

dp[i]表示nums[0-i]的连续子数组的最大和。

2.递推公式：

dp[i]只有两个方向可以推出来：

dp[i-1]+nums[i]，即nums[i]加入当前连续子数组和；

nums[i]，即从头开始计算连续子数组和。

所以dp[i] = max(dp[i - 1] + nums[i], nums[i])。

3.初始化：

初始化dp[0]=nums[0]。

4.确定遍历顺序：从前向后遍历。

5.举例推导dp数组：

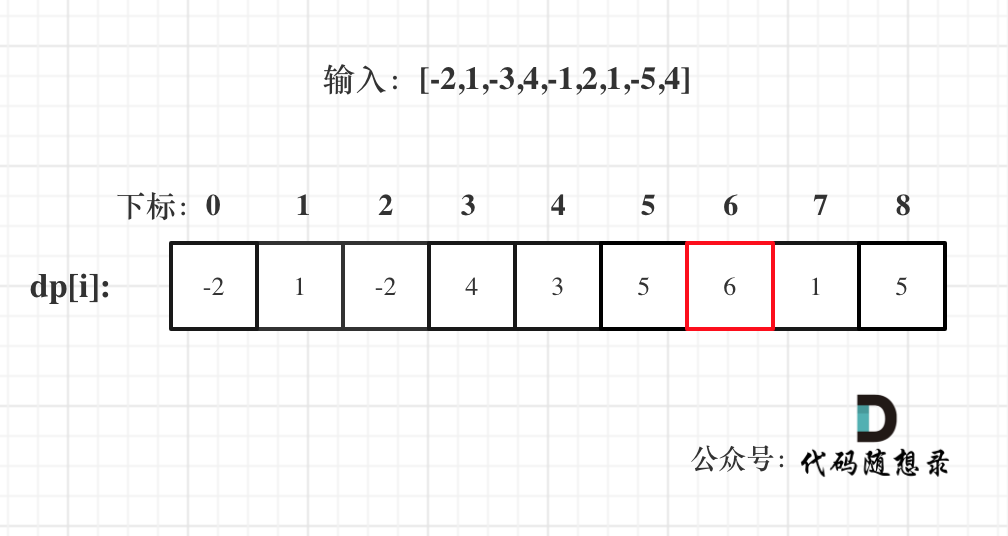
代码如下：

class Solution {
    public int maxSubArray(int[] nums) {
        //动态规划
        int n=nums.length;
        int[] dp=new int[n];
        dp[0]=nums[0];
        int res=dp[0];
        for(int i=1;i<n;i++){
            dp[i]=Math.max(dp[i-1]+nums[i],nums[i]);
            res=Math.max(res,dp[i]);
        }
        return res;
    }
}

LeetCode 392 判断子序列

题目链接：392. 判断子序列 - 力扣（LeetCode）

给定字符串 s 和 t ，判断 s 是否为 t 的子序列。

字符串的一个子序列是原始字符串删除一些（也可以不删除）字符而不改变剩余字符相对位置形成的新字符串。（例如，"ace"是"abcde"的一个子序列，而"aec"不是）。

示例 1：

输入：s = "abc", t = "ahbgdc"
输出：true
示例 2：

输入：s = "axc", t = "ahbgdc"
输出：false

这个题本质和求两个字符串的最长公共子序列是一样的，只不过最后判断最长公共子序列的长度等于s的长度就返回true，否则返回false。

代码如下：

class Solution {
    public boolean isSubsequence(String s, String t) {
        int m=s.length();
        int n=t.length();
        int[][] dp=new int[m+1][n+1];
        for(int i=1;i<=m;i++){
            for(int j=1;j<=n;j++){
                if(s.charAt(i-1)==t.charAt(j-1))dp[i][j]=dp[i-1][j-1]+1;
                else dp[i][j]=Math.max(dp[i-1][j],dp[i][j-1]);
            }
        }
        if(dp[m][n]==m)return true;
        else return false;
    }
}

LeetCode 115 不同的子序列

题目链接：115. 不同的子序列 - 力扣（LeetCode）

给你两个字符串 s 和 t ，统计并返回在 s 的子序列中 t 出现的个数。

测试用例保证结果在 32 位有符号整数范围内。

示例 1：

输入：s = "rabbbit", t = "rabbit"
输出：3
解释：
如下所示, 有 3 种可以从 s 中得到 "rabbit" 的方案。
rabbbit
rabbbit
rabbbit

示例 2：

输入：s = "babgbag", t = "bag"
输出：5
解释：
如下所示, 有 5 种可以从 s 中得到 "bag" 的方案。
babgbag
babgbag
babgbag
babgbag
babgbag

这个题可以等价于判断有多少种方式删减s可以得到t。

1.确定dp数组以及下标的含义：

dp[i][j]表示s的前i个元素通过删减可以得到t的前j个元素的方法。

2.递推公式：

如果s[i-1]==t[j-1]，那么dp[i][j]有两种可能：

一种是保留下s[i-1]，也就是s的前i-1个元素通过删减可以得到t的前j-1个元素的方法；

一种是不保留s[i-1]，也就是s的前i-1个元素通过删减可以得到t的前j个元素的方法。

所以dp[i][j]=dp[i-1][j-1]+dp[i-1][j]。

如果s[i-1]！=t[j-1]，那么dp[i][j]只有一种可能，也就是s的前i-1个元素通过删减可以得到t的前j个元素的方法，即dp[i][j]=dp[i-1][j]。

3.初始化：

初始化dp[i][0]=1（0<=i<=m），表示当t为空字符串时，s只有一种方法可以得到t，那就是全部删减掉；初始化dp[0][j]=0（1<=j<=n），表示当s为空字符串时，除非t也为空字符串，否则s永远无法得到t。

4.确定遍历顺序：行优先从前向后遍历。

5.举例推导dp数组：

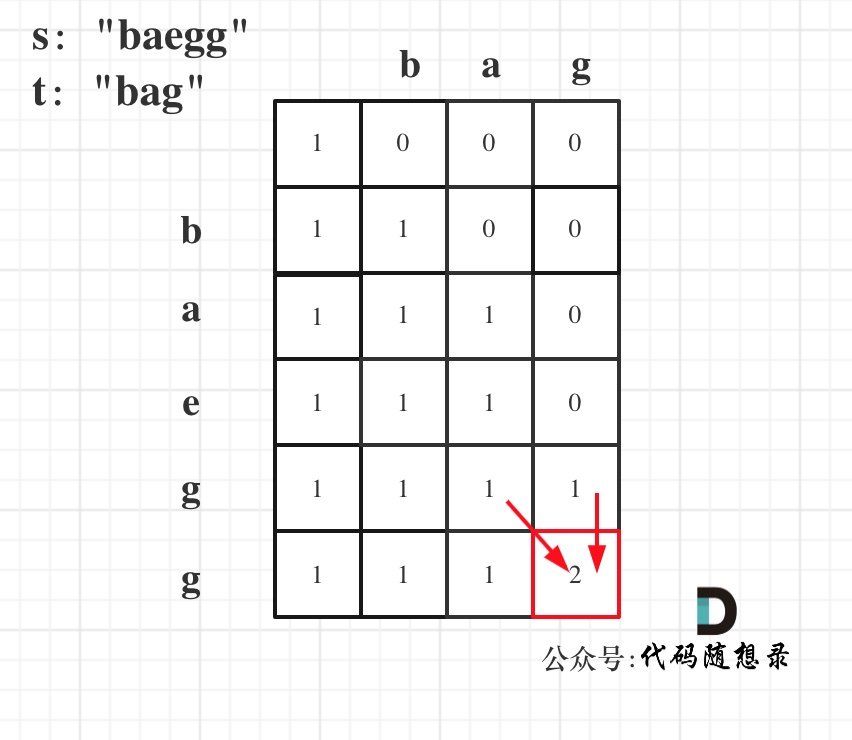
代码如下：

class Solution {
    public int numDistinct(String s, String t) {
        int m=s.length();
        int n=t.length();
        int[][] dp=new int[m+1][n+1];
        for(int i=0;i<=m;i++)dp[i][0]=1;
        for(int i=1;i<=m;i++){
            for(int j=1;j<=n;j++){
                if(s.charAt(i-1)==t.charAt(j-1))dp[i][j]=dp[i-1][j-1]+dp[i-1][j];
                else dp[i][j]=dp[i-1][j];
            }
        }
        return dp[m][n];
    }
}

LeetCode 583 两个字符串的删除操作

题目链接：583. 两个字符串的删除操作 - 力扣（LeetCode）

给定两个单词 word1 和 word2 ，返回使得 word1 和 word2 相同所需的最小步数。

每步可以删除任意一个字符串中的一个字符。

示例 1：

输入: word1 = "sea", word2 = "eat"
输出: 2
解释: 第一步将 "sea" 变为 "ea" ，第二步将 "eat "变为 "ea"
示例 2:

输入：word1 = "leetcode", word2 = "etco"
输出：4

1.确定dp数组以及下标的含义：

dp[i][j]表示word1的前i个元素和word2的前j个元素想要相同需要的最小步数。

2.递推公式：

当word1[i-1]==word2[j-1]时，dp[i][j]只有一种可能，也就是word1的前i-1个元素和word2的前j-1个元素想要相同需要的最小步数，即dp[i][j]=dp[i-1][j-1]。

当word1[i-1]！=word2[j-1]时，dp[i][j]有三种可能：

一种是word1的前i-1个元素和word2的前j个元素想要相同需要的最小步数+1，也就是把word1[i-1]删掉；word1的前i个元素和word2的前j-1个元素想要相同需要的最小步数+1，也就是把word2[j-1]删掉；word1的前i-1个元素和word2的前j-1个元素想要相同需要的最小步数+2，也就是把两个都删掉。

所以dp[i][j] = min(dp[i - 1][j - 1] + 2, dp[i - 1][j] + 1, dp[i][j - 1] + 1)，又因为dp[i][j - 1] + 1 = dp[i - 1][j - 1] + 2，所以可以简化为：dp[i][j] = min(dp[i - 1][j] + 1, dp[i][j - 1] + 1)。

3.初始化：

初始化dp[i][0]=i（1<=i<=m），表示当word2为空字符串时，word1需要删除i个元素才能和word2相同；同样的,dp[0][j]=j（1<=j<=n）。

4.确定遍历顺序：行优先从前向后遍历。

5.举例推导dp数组：

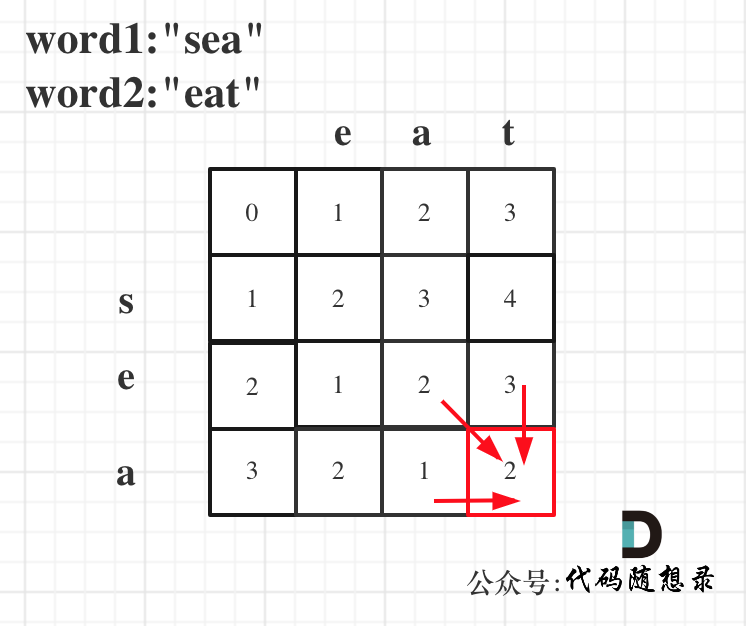
代码如下：

class Solution {
    public int minDistance(String word1, String word2) {
        int m=word1.length();
        int n=word2.length();
        int[][] dp=new int[m+1][n+1];
        for(int i=1;i<=m;i++)dp[i][0]=i;
        for(int j=1;j<=n;j++)dp[0][j]=j;
        for(int i=1;i<=m;i++){
            for(int j=1;j<=n;j++){
                if(word1.charAt(i-1)==word2.charAt(j-1))dp[i][j]=dp[i-1][j-1];
                else dp[i][j]=Math.min(dp[i-1][j]+1,dp[i][j-1]+1);
            }
        }
        return dp[m][n];
    }
}

LeetCode 72 编辑距离

题目链接：72. 编辑距离 - 力扣（LeetCode）

给你两个单词 word1 和 word2， 请返回将 word1 转换成 word2 所使用的最少操作数 。

你可以对一个单词进行如下三种操作：

插入一个字符
删除一个字符
替换一个字符

示例 1：

输入：word1 = "horse", word2 = "ros"
输出：3
解释：
horse -> rorse (将 'h' 替换为 'r')
rorse -> rose (删除 'r')
rose -> ros (删除 'e')
示例 2：

输入：word1 = "intention", word2 = "execution"
输出：5
解释：
intention -> inention (删除 't')
inention -> enention (将 'i' 替换为 'e')
enention -> exention (将 'n' 替换为 'x')
exention -> exection (将 'n' 替换为 'c')
exection -> execution (插入 'u')

这个题和上一题不同之处在于不止可以删除元素，还可以替换、插入，但实际上插入元素和删除元素本质是一样的，所以我们只需再独立考虑一个替换元素的情况。

当word1[i-1]==word2[j-1]时，dp[i][j]依旧只可能等于dp[i-1][j-1]；

当word1[i-1]!=word2[j-1]时，dp[i][j]有三种可能：

一种是删除word1[i-1]（或者在word2[j]之前插入word1[i-1]），也就是dp[i][j]=dp[i-1][j]；

一种是删除word2[j-1]（或者在word1[i]之前插入word2[j-1]），也就是dp[i][j]=dp[i][j-1]；

一种是替换word1[i-1]为word2[j-1]，也就是dp[i][j]=dp[i-1][j-1]+1。

所以 dp[i][j]=min(dp[i-1][j]+1,dp[i][j-1]+1,dp[i-1][j-1]+1)。

class Solution {
    public int minDistance(String word1, String word2) {
        int m=word1.length();
        int n=word2.length();
        int[][] dp=new int[m+1][n+1];
        for(int i=0;i<=m;i++)dp[i][0]=i;
        for(int j=1;j<=n;j++)dp[0][j]=j;
        for(int i=1;i<=m;i++){
            for(int j=1;j<=n;j++){
                if(word1.charAt(i-1)==word2.charAt(j-1))dp[i][j]=dp[i-1][j-1];
                else dp[i][j]=Math.min(dp[i-1][j]+1,Math.min(dp[i][j-1]+1,dp[i-1][j-1]+1));
            }
        }
        return dp[m][n];
    }
}