2023蓝桥杯第十四届国赛：数数 ； 2024的质因数

相关知识

 

1. 质数：又称素数，指的是在大于1的自然数中，除了1和它自身外，不能被其他自然数整除的数。比如2、3、5、7、11等都是质数（素数）。
2. 因数：是指整数a除以整数b（b≠0）的商正好是整数而没有余数，此时称b是a的因数。例如，12÷3 = 4，3能够整除12且没有余数，所以3是12的因数。
3. 质因数：在数论里是指能整除给定正整数的质数。对于12，它可以分解为12=2*2*3，其中2和3是质数，即2和3就是12的质因数。

 

数数 

问题描述

任何一个大于 1 的正整数都能被分解为若干个质数相乘, 比如 28=2×2×7被分解为了三个质数相乘。请问在区间 [2333333, 23333333] 中有多少个正整数 可以被分解为 12 个质数相乘?

答案提交

这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一 个整数, 在提交答案时只填写这个整数, 填写多余的内容将无法得分。

运行限制

• 最大运行时间：1s
• 最大运行内存: 512M

 

 

 

 

题解1

 

当我们需要找到一个区间中满足某种条件的数的个数时，一种常见的方法是使用暴力枚举。然而，该区间的范围非常大，导致代码超时。

该代码提交会因为超时显示不通过：

 

在Dev上运行大约20多s会出结果。

 

由于是填空题，我们只提交结果即可。

 

 

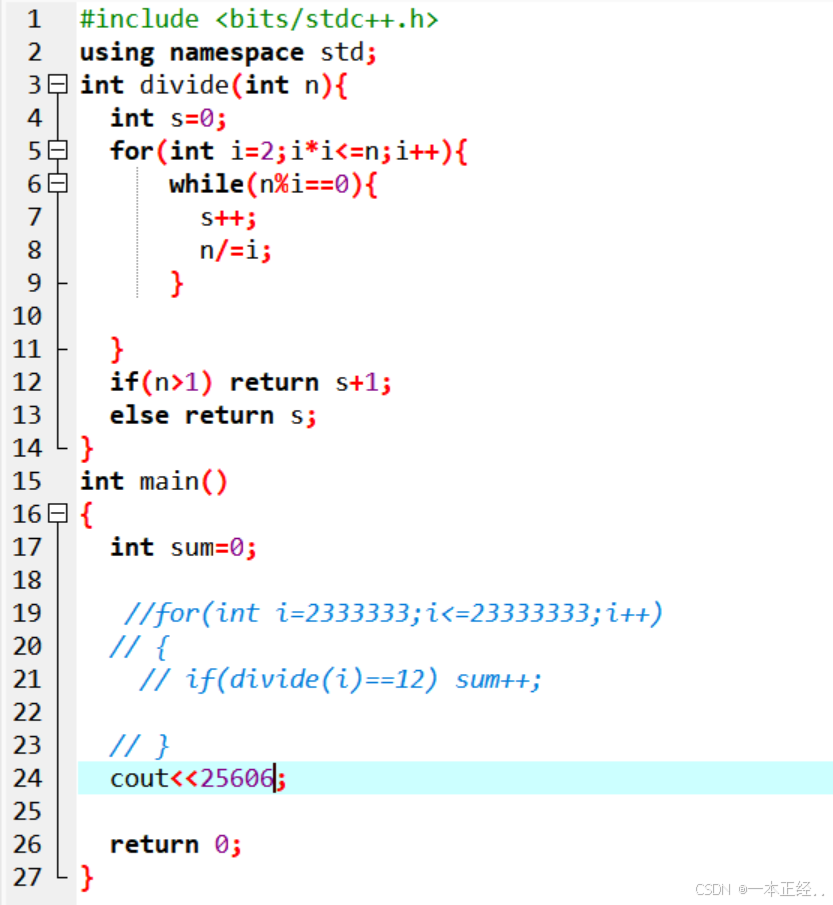
题解2

考察的算法知识

 

• 埃拉托斯特尼筛法（部分思想体现）：代码中通过标记数组s来筛选出一些特殊的数字（虽然不完全是标准的埃氏筛用于筛质数的完整逻辑，但有类似通过标记来筛选的思想），比如最初将未标记（s[i]为0）的数字进行特殊处理（如加入p向量等），后续又基于已有的特殊数字（p中的元素）来标记它们的倍数等，整体有点类似埃氏筛利用已有质数标记合数的思路，不过这里标记的逻辑和含义更复杂一些，不完全等同于筛质数。
• 线性筛（也有部分影子）：在通过已有特殊数字标记其倍数的过程中（for(auto x : p)循环内的操作），通过及时break避免重复标记（比如x * i > R就跳出），有一点线性筛优化标记过程、避免重复处理的思想，不过同样这里整体逻辑和标准线性筛还是有差异，只是借鉴了部分避免重复操作的思路来构建自己的标记体系。

 

这里运用了算法知识，本人萌新，了解甚少，会继续学习。。。

 

 

 

 

 

 

 

 

2024的质因数 

   问题描述

如果一个数p是个质数，同时又是整数a的约数，则 p称为a的一个质因数。

请问2024有多少个质因数。

  答案提交

这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

 

 

题解

考察循环

循环枚举2024每一个因数，并且判断是否为质数即可。

判断质数的方法：平方根判断法，直接判断法，预处理法。

以下为平方根判断法：

 

输出：

 

 

可得2024的质因数分别是2，11，23。

 

其他

当求 数n 有几个质因数可用：

 

 

 

欢迎指正不足。