第一章-计算机基础知识（第二节-计算机中的信息表示）

根据数学推导证明，当N=e(自然数)=2.71时，表示同样信息量所使用的设备量是最少的。e介于整数2和3之间，由于三值元件比二值元件少得多，这也是机器内主要采用二进制的道理所在。总之，二进制编码形式易于实现，运算简单、可靠，二进制应用于计算机是必然结果。但二进制计数书写冗长，不便阅读和记忆为此常常约简为八进制或十六进制。学习计算机就需要熟练地掌握这些进位计数制和它们之间的换算关系。

二．数制及其转换

(一)数制

数制是指用一组固定的符号和统一的规则来表示数值的方法。其中，按照进位方式计数的数制称为进位计数制。在日常生活中，人们习惯用的进位计数制是十进制，而计算机则使用二进制，除此以外，还包括八进制和十六进制等。二进制顾名思义，就是逢二进一的数字表示方法;依此类推，十进制就是逢十进一，八进制就是逢八进一等。

进位计数制中每个数码的数值不仅取决于数码本身，其数值的大小还取决于该数码在数中的位置，如十进制数828.41，整数部分的第1个数码“8”处在百位表示800，第2个数码“2”处在十位，表示20,第3个数码“8”处在个位，表示8小数点后第1个数码“4”处在十分位，表示0.4，小数点后第2个数码“1”处在百分位，表示0.01。也就是说，处在不同位置的数码所代表的数值不相同，分别具有不同的位权值，数制中数码的个数称为数制的基数，十进制数有0、1、2、3、4、5、6、7、8、9共10个数码,其基数为10。

无论在何种进位计数制中，数都可写成按位权展开的形式，如十进制数828.41可写成下式。

上式称为数值的按位权展开式，其中10称为十进制数的位权数，其基数为10使用不同的基数，便可得到不同的进位计数制。设R表示基数，则称为R进制，使用R个基本的数码，R"就是位权，其加法运算规则是“逢R进一”，任意一个R进制数D均可以展开表示如下。

(二)数制的转换

1.非十进制数转换为十进制数

将二进制数、八进制数和十六进制数转换为十进制数时，只需用该数制的各位数乘以各白位权数，然后将乘积相加，用按权展开的方法即可得到对应的结果。

二进制100110转化为十进制数：

2.十进制数转换为非十进制数

十进制数转换为非十进制数分为两部分进行，整数部分和小数部分，分开转换后再以小数点为结合点组合起来。

整数部分:除以基数取余倒--除以基数取余，直至商为0，余数按先后顺序从低位到高位排列。

小数部分:乘基数取整顺--乘基数取整，直至达到所要求的精度或小数部分为0，整数按先后顺序从高位到低位排列。

例:将-进制数121.8125和687.5分别转换为二进制数和十六进制数。

注意:在进行小数部分的转换时，有些十进制小数不能转换为有限位的二进制小数，此时只能用近似值表示。(0.57 )10不能用有限位二进制数表示如要求5位小数近似值，则得到(0.57)10≈(0.10010)2。

3.二/八/十六进制数的互相转换

由于一位八/十六进制数相当于三/四位二进制数，因此，要将八/十六进制数转换成二进制数时，只需以小数点为界，向左或向右每一位八/十六进制数用相应的三/四位二进制数取代即可。如果不足三/四位，可用零补足。反之，二进制数转换成相应的八/十六进制数，只是上述方法的逆过程，即以小数点为界，向左或向右，每三/四位二进制数用相应的一位八/十六进制数取代即可。

(1)八进制数转换成二进制数

八进制数转换成二进制数的转换原则是"一分为三”，即从八进制数的低位开始，将每一位上的八进制数写成对应的3位二进制数即可。如有小数部分，则从小数点开始，分别向左右两边按上述方法进行转换即可。

(2)二进制数转换成八进制数

二进制数转换成八进制数所采用的转换原则是“3位分一组”，即以小数点为界，整数部分从右向左每3位为一组，若最后一组不足3位，则在最高位前面添0补足3位;小数部分从左向右每3位分为一组，最后一组不足3位时，尾部用0补足3位然后将每组中的二进制数按权相加得到对应的八进制数。

(3)十六进制数转换成二进制数

十六进制数转换成二进制数的转换原则是"一分为四”，即把每一位上的十六进制数写成对应的4位二进制数即可。

(4)二进制数转换成十六进制数

二进制数转换成十六进制数所采用的转换原则与上面的类似，为“4位分一组”，即以小数点为界，整数部分从右向左、小数部分从左向右每4位一组，不足4位用0补齐即可。

4.二进制数的运算

(1)二进制的算术运算

进制的算术运算也就是通常所说的四则运算，包括加、减、乘、除，运算比较简单，其具体运算规则如下。

加法运算:按“逢二进一”法，向高位进位,运算规则为0+0=0、0+1=1、1+0=1、1+1=10.

减法运算:减法实质上是加上一个负数，主要应用于补码运算，运算规则为0-0=0、1-0=1、0-1=1(向高位借位，结果本位为1)、1-1=0。

(2)二进制的逻辑运算

计算机所采用的二进制数1和0可以代表逻辑运算中的“真”与“假”、“是”与“否”和“有”与“无”。二进制的逻辑运算包括“与”“或”“非”“异或”4种，具体介绍如下。

“与”运算:“与”运算又称为逻辑乘,通常用符号“x”“^”".”来表示其运算法则为0^0=0、0^1=0、1^0=0、1^1=1。通过上述法则可以看出，当两个参与运算的数中有一个数为0时，其结果也为0，此时是没有意义的，只有当数中的数值都为1时，结果为1，即只有当所有的条件都符合时，逻辑结果才为肯定值。例如，假定某一个公益组织规定加入成员的条件是女性与慈善家，那么只有既是女性又是慈善家的人才能加入该组织。

“或”运算:“或”运算又称为逻辑加，通常用符号“+”或“v”来表示其运算法则为0v0=0、0v1=1、1v0=1、1v1=1。该法则表明只要有一个数为1则结果就是1。例如，假定某一个公益组织规定加入成员的条件是女性或慈善家那么只要符合其中任意一个条件或两个条件都可以加入该组织。

“非”运算:“非”运算又称为逻辑否运算,通常是在逻辑变量上加上划线来表示，如变量为A，则其非运算结果用表示。其运算法则为0=1、1=0。例如，假定A变量表示男性，就表示非男性，即指女性。

三．信息在计算机中的存储

数据是计算机处理的对象，是对客观事物的一种符号表示,

从外部形式来看，计算机可以处理数值、文本、图像、声音、视频等。但是在计算机系统的内部，这些都不能直接由计算机进行处理和存储，它们必须采取特殊的表示形式才能由计算机进行加工处理。这种特殊的形式就是二进制编码形式即采用二进制编码来表示数值、文字、图像、声音和视频等

(一)位

计算机中所有的数据都是以二进制来表示的，一个二进制代码称为一位或一比特(bit)，记为b。位是计算机中最小的信息单位。

(二)字节

在对二进制数据进行存储时，以8位二进制代码为一个单元存放在一起，称为一个Byte(字节)，记为B，它是计算机中最基本的存储单位，同时也是衡量存储器大小的单位，例如U盘为16GB。

(三)容量单位的转换关系

1B=8bit;1KB=2的10次B=1024B;

1MB=2的20次B=1024KB;

1GB=2的30次B=1024MB;

1TB=1024GB,1PB=1024TB,1EB=1024PB

1ZB=1024EB,1YB=1024ZB,1BB=1024YB.

采用210数量级往上增加，即千字节(KB)，兆字节(MB)、吉字节(GB)太字节(TB)、拍字节(PB)、艾字节(EB)、泽字节(ZB)和字节(YB)等等。随着大数据时代的到来，每天产生的数据量都在数个拍字节以上。

四、计算机中常见的数据表示

(一)机器数

由于计算机采用二进制，所以任何类型的数据都必须转换为二进制。数值型数据指数学中的代数值，具有量的含义，同时有正负、整数和小数之分。要在计算机中表示一个数值型，除了必须先将它转换为二进制数外，还要考虑数据的存储长度符号以及小数点问题。

理论上讲，一个数不论有多少有效位数，计算机都能表示，由于计算机资源有限，考虑到制造成本和实现的可能性，一般用于存放一个数的电子器件位数总是有限的和固定的，其二进制位数称为字长，即指CPU一次所能处理的二进制数据的位数。可同时处理的位数越多，CPU的档次就越高，从而它的功能就越强，速度也越快。在计算机表示一个数时，不但要考虑其大小，还要考虑用多少个字长来存放。

数有正、负之分。在计算机中，只有数码1和0两种不同的状态，为了统一起见，通常在计算机中，用0表示正数，用1表示负数。且用最高位作为数值的符号位也就是，符号占用一个二进制位。例如，如果采用8位字长，来表示二进制数。则最高位为符号位，其余7位表示数据大小。这种连同数字与符号组合在一起的二进制数称为机器数，由机器数所表示的实际值称为真值。

在计算机中，机器数的表示有两种:一是定点表示法，即小数点的位置是固定不变的;二是浮点表示法，即小数点的位置是可浮动的。实数包括整数和小数，整数一般采用定点表示法，即规定数的最后一位为小数点所在位置。纯小数也可以采用定点法，即人为规定小数点在符号位之后，但为了计算方便和统一起见，带有小数的实数，包括纯小数，一般都采用浮点表示法,

1.整数定点表示法

在计算机中，整数定点表示的机器码通常有原码、反码和补码三种表示方式。对于有符号的整数，用“0”表示正数，用“1”表示负数,符号位设置在机器码的最高位。任何正数的原码、反码和补码的形式完全相同，负数则各有不同的表示形式。

(1)原码

用8位二进制数表示数的原码时，最高位为数的符号位，其余7位为数值位。

对于零，可以认为它是正零，也可以认为它是负零，所以零的原码有两种表示形式:

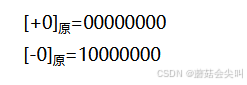
8位二进制数原码表示范围为:11111111~01111111，即-127~+127，共可以表示255个数，其中0有两种表示方法，分别是00000000和10000000。

如果是n位二进制原码，则其表示范围为-( 2的n-1次-1)~+(2的n-1次-1)。

(2)反码

在反码表示方法中，正数的反码与原码相同，负数的反码由它对应原码除符号位之外，其余各位按位取反得到。例如：

(3)补码

补码的概念:先以钟表对时为例，假设现在的标准时间为5点整，而有一只表却已是7点，为了校准时间，可以采用两种方法:一是将时针退2格，即7-2=5;一是将时针向前拨10格，即7+10=12(自动丢失)+5，都能对准到5点。可见，减2和加10是等价的，我们把(+10)称为(-2)对12的补码，12为，当数值大于模12时可以丢弃12。也就是说，在表盘中是以12为模的，任何一个时刻加上一个12的整数倍，时针位置不变。

在补码表示方法中，正数的补码与原码相同，负数的补码采用求补运算得到即对负数所对应的原码除符号位之外，其余各位按位取反且末位加一得到，或者用模加上该数而得的二进制数码。

8位二进制数补码表示范围为:10000000~01111111，即-128~+127，其中0只有一种表示方法，另外表示-128的机器数10000000是一个特殊情况。如果是n位二进制原码表示范围为-2的n-1次~+(2的n-1次-1)。

2.实数浮点表示法

实数既有整数部分，也有小数部分，整数和纯小数是实数的特例，168.9、-1.689、0.01689、1689都是实数。基本数字相同，所不同的是小数点位置不同而已。如果实数都表示成一个纯小数和一个幂之积，则上述实数可以表示为0.1689x103、-0.1689x101、0.1689x10-1和0.1689x104。在这种表示方法下我们只关心数字和指数即可。

可见任何一个实数，在计算机中表示时，都可以用一个纯小数的“尾数”来表示有效数字，而用整数的阶码表示“指数”，尾数和阶码都为有符号数，通过阶码的大小确定小数点的位置，这种用尾数和指数来表示实数的方法叫做“浮点表示法”，计算机中的实数也叫做“浮点数”

尾数的位数决定数的精度，指数的位数决定数的范围，根据占用字节数的多少不同还可以分为单精度浮点数和双精度浮点数。浮点数的长度越长，可表示的数的范围越大，精度也越高。

(二)ASCII码

ASCII码是“美国信息交换标准代码”(AmericanStandard Code forInformationInterchange)的简称，是国际上广泛采用的一种编码字符集。ASCII码使用指定的7位或8位二进制数组合来表示128或256种可能的字符。标准ASCII码也叫基础ASCII码，使用7位二进制数来表示所有的大写和小写字母，数字0到9标点符号，以及在美式英语中使用的特殊控制字符。

其中:

0~31及127(共33个)是控制字符或通信专用字符(其余为可显示字符),如控制符:LF(换行)、CR(回车)、FF(换页)、DEL(删除)、BS(退格)、BEL(响铃)等;通信专用字符:SOH(文头)、EOT(文尾)、ACK(确认)等;

ASCII值为8、9、10和13分别转换为退格、制表、换行和回车字符它们并没有特定的图形显示，但会依不同的应用程序，而对文本显示有不同的影响。

32~126(共95个)是字符(32是空格)，其中48~57为0到9十个阿拉伯数字，65~90为26个大写英文字母，97~122号为26个小写英文字母，其余为一些标点符号、运算符号等。

在标准ASCHI中，其最高位(b7)用作奇偶校验位。所谓奇偶校验，是指在代码传送过程中用来检验是否出现错误的一种方法，一般分奇校验和偶校验两种。

奇校验规定:正确的代码一个字节中1的个数必须是奇数，若非奇数，则在最高位b7添1;

偶校验规定:正确的代码一个字节中1的个数必须是偶数，若非偶数，则在最高位b7添1。后128个称为扩展ASCII码，目前许多基于x86的系统都支持使用扩展ASCII。扩展ASCII码允许将每个字符的第8位用于确定附加的128个特殊符号字符外来语字母和图形符号。

(三)汉字编码

汉字编码处理与西文的区别很大，根据处理阶段的不同，可将汉字编码分为输入码、显示字形码、机内码和交换码。汉字输入码如今已经有数百种广泛应用的包括自然码、全/双拼音码、五笔字型码等。目前，表示汉字字形常用矢量法与点阵字形法。汉字的输入码、字形码、机内码均不是唯一的不方便进行不同计算机系统之间的汉字信息交换。