1——欧几里得算法
两个整数a,b(a>=b)的最大公约数集合与a mod b和b的公约数集合相同,可得gcd(a,
b)=gcd(b,a mod b)
//计算最大公约数,又称辗转相除法
int gcd(int a,int b)
{
if(b==0)return a;
else return gcd(b,a%b);
}
int gcd(int a,int b)
{
return (b==0)?a:gcd(b,a%b);
}
 2——解线性方程(欧几里得扩展法解方程)
2——解线性方程(欧几里得扩展法解方程)
ax+bx=gcd(a,b)







扩展欧几里得算法
int extend_gcd(int a,int b,int &x,int &y)
{
if(b==0)
{
x=1;y=0;
return a;
}else
{
int ret=extend_gcd(b,a%b,y,x);
y-=x*(a/b);
return ret;
}
}使用扩展欧几里得算法求解逆元
int inverse(int a,int b){
int x,y;
extend_gcd(a,b,x,y);
return x;
}使用欧拉定理求逆元



int power_mod(int a,int b,int n)
{
int ret=1;
while(b){
if(b&1)ret=(long long)ret*a%n;
a=(long long)a*a%n;
b>>=1;
}
return ret;
}线性求逆元:递推法

线性求逆元:倒推法












 模板
模板
#include <iostream>
#include<cstdio>
#include<cstring>
using namespace std;
int ex_gcd(int aa, int bb, int& xx, int& yy)//递归
{
if (bb == 0) { xx = 1; yy = 0; return aa; }
int ans = ex_gcd(bb, aa % bb, xx, yy);
int temp = xx;
xx = yy;
yy = temp - aa / bb * yy;
return ans;
}
int main()
{
int a, b, c;
scanf_s("%d%d%d", &a, &b, &c);
int x, y;//求第一个特解
int res = ex_gcd(a, b, x, y);
if (c % res)printf("Impossible\n");
else {
int x0 = x * c / res;//求第二个特解
int y0 = y * c / res;
int L = b / res;
if (L < 0)L = -L;
int X = (x0 % L + L) % L;//求x通解里的最小正整数
int Y = (c - a * X) / b;
printf("x最小正整数解时 : x = %d,y = %d\n", X, Y);
}
return 0;
}#include <iostream>
#include <cstdio>
using namespace std;
int ex_gcd(int aa, int bb, int& xx, int& yy) {
if (bb == 0) { xx = 1; yy = 0; return aa; }
int ans = ex_gcd(bb, aa % bb, xx, yy);
int temp = xx;
xx = yy;
yy = temp - aa / bb * yy;
return ans;
}
int main() {
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
int x, y;
int res = ex_gcd(a, b, x, y);
if (res == 0 && c != 0) {
printf("Impossible\n");
} else {
int t = c / res;
int x0 = x * t;
int y0 = y * t;
// 找到x的最小正整数解
int L = abs(b / res);
x0 = (x0 % L + L) % L;
// 使用x的解来计算y的解
int Y = (c - a * x0) / b;
printf("x最小正整数解时 : x = %d, y = %d\n", x0, Y);
}
return 0;
}扩展gcd代码实现
#include<iostream>
using namespace std;
typedef long long ll;
ll ex_gcd(ll a, ll b, ll& x, ll& y)
{
ll GCD, t;
if (!b) {
x = 1; y = 0;
return a;
}
GCD = ex_gcd(b, a % b, x, y);
t = x;
x = y;
t - (a / b) * y;//回溯
}
ll inv(int a, int mod)//求a模mod的逆元
{
ll x, y;
ll GCD = ex_gcd(a, mod, x, y) % mod;
return GCD ? (x % mod + mod) % mod : -1;
}
ll solve_ex_gcd(ll a, ll b, ll c, ll& x, ll& y)//求解
{
ll d = ex_gcd(a, b, x, y);
if (c % d != 0) {//无整数解
x = -1;
y = -1;
return -1;
}
x *= (c / d);
b = abs(b / d);
while (x < 0) {
x += b;
}
y = (c - a * x) / b;
return 0;
}
int main()
{
ll x, y, a, b, c;
cin >> a >> b >> c;
solve_ex_gcd(a, b, c, x, y);
cout << x << endl;
return 0;
}3——因式分解与算术基本定理
1、p是素数,p|ab,则p|a或p|b或者p|a且p|b
2、每个整数n>=2可唯一分解成素数乘积
3、要将n表示素数乘积,用小于等于sqrt(n)的每个数试除它,如果没有求得整除n的整数,则n本身是素数,否则求得的第一个数是素数p,分解n=mp,对m重复这个过程
素数判定
//判定素数
#include<iostream>
using namespace std;
bool isPrime(int a) {
if (a < 2)return 0;
for (int i = 2; i * i <= a; i++)
{
if (a % i == 0)return 0;
}
return 1;
}




 4——同余方程
4——同余方程
a=b(mod m)
m|(a-b)
a+a1=b+b(mod m)(条件:gcd(a,b)=1)
ac=bc(mod m)

#include<iostream>
using namespace std;
int ex_gcd(int a, int b, int& x, int& y)
{
if (b == 0) {
x = 1;
y = 0;
return a;
}
int d = ex_gcd(b, a % b, x, y);
int temp = x;
x = y;
y = temp - a / b * y;
return d;
}
bool liEu(int a, int b, int c, int& x, int& y)
{
int d = ex_gcd(a, b, x, y);
if (c % d != 0)return 0;//无解
int k = c / d;
x *= k;
y *= k;
// 通过扩展欧几里得算法得到的x, y可能不是最小正整数解,需要调整
x = (x % (b / d) + (b / d)) % (b / d); // 保证x是非负且小于b/d
return 1;
}5——费马小定理和欧拉函数
p is prime,a!=0(mod p)
->a^(p-1)=1(mod 23)



//类似于分解质因数,计算答案即可。
//参考代码 (时间复杂度 O(n)):
int phi(int x) {
int res = x;
for (int i = 2; i * i <= x; i ++) {
if (x % i == 0) {
res = res / i * (i - 1);
while (x % i == 0) {
x /= i;
}
}
}
if (x > 1) {
res = res / x * (x - 1);
}
-
初始化
res为x,因为如果没有任何因子能整除x(即x是质数),那么phi(x) = x - 1。 -
遍历从 2 到
sqrt(x)的所有整数i。对于每个i,检查x是否能被i整除。 -
如果
x能被i整除,那么i是x的一个质因子。根据欧拉函数的性质,phi(x)需要除以i并乘以i-1,因为对于x的每一个i的倍数(除了i本身),它都不能与x互质。然后,通过循环不断除以i,直到x不再能被i整除,以确保我们处理了x中所有i的因子。 -
循环结束后,如果
x大于 1,说明x是一个质数(因为它没有被之前的任何i整除)。此时,我们需要将res除以x并乘以x-1,因为此时x的所有小于它的正整数(除了 1 和x本身)都与其互质。 -
函数返回
res,即phi(x)的值。
6——中国剩余定理
#include<iostream>
using namespace std;
//扩展gcd
int ex_gcd(int a, int b, int& x, int& y)
{
if (b == 0) {
x = 1; y = 0; return a;
}
int d = ex_gcd(b, a % b, x, y);
int t = x;
x = y;
y = t - a / b * y;
return d;
}
//利用ec_gcd求逆元
int inv(int a, int b) {
int x, y;
ex_gcd(a, b, x, y);
return x;
}
//Chinese Remainder Theorem
int CRT(const int a[], const int m[], int n)
{
int M = 1, ret = 0;
for (int i = 1; i <= n; i++)M *= m[i];
for (int i = 1; i <= n; i++) {
int Mi = M / m[i], ti = inv(Mi, m[i]);
ret=(ret + a[i] * Mi * ti) % M;
}
return ret;
}






7——欧拉公式

8——素数
![]()
![]()

9——素数计数


![]()
![]()
10——幂模m与逐次平方(快速幂)
a^b
//递归法求a^b
long long binpow(long long a, long long b)
{
if (b == 0)return 1;
long long res = binpow(a, b / 2);
if (b & 1) return res * a;
else
return res * res * a;
}
//非递归法
long long binpow(long long a, long long b)
{
long long res = 1;
while (b)
{
if (b & 1)res *= a;
a *= a;
b >>= 1;
}
return res;
}a^b(mod p)
long long binpow(long long a, long long b,long long p)
{
long long res = 1;
a = a % p;
while (b)
{
if (b & 1)res = res * a % p;
a=a*a%p;
b >>= 1;
}
return res;
}11——计算模m的k次根

#include<iostream>
#include<vector>
#include<cmath>
using namespace std;
// 扩欧求逆元
int ex_gcd(int a, int b, int& u, int& v) {
if (b == 0) {
u = 1; v = 0; return a;
}
int d = ex_gcd(b, a % b, u, v);
int t = u;
u = v;
v = t - a / b * v;
return d;
}
int inv(int a, int b) {
int x, y;
int g = ex_gcd(a, b, x, y);
if (g != 1) return -1; // 如果a和b不互质,则返回-1或抛出异常
x = (x % b + b) % b; // 保证x是正数
return x;
}
// 求m的欧拉函数
int phi(int m) {
int phi_m = m;
for (int i = 2; i * i <= m; i++) {
if (m % i == 0) {
phi_m = phi_m / i * (i - 1);
while (m % i == 0) m /= i;
}
}
if (m > 1) phi_m = phi_m / m * (m - 1); // 处理m本身是一个质数的情况
return phi_m;
}
// 求b^k(mod m)
int binpow(int a, int b, int p) {
int res = 1;
a %= p;
while (b) {
if (b & 1) res = res * a % p;
a = a * a % p;
b >>= 1;
}
return res;
}
int main() {
int k, m, b, x, y;
cin >> k >> b >> m;
// 求m的欧拉函数
int phi_m = phi(m);
cout << "phi(" << m << ") = " << phi_m << '\n';
// 检查k和phi_m是否互质
if (ex_gcd(k, phi_m, x,y ) != 1) {
cout << "k和phi(m)不互质,无法找到逆元。\n";
return 1;
}
// 求ku=1(mod phi_m)的解即求k(mod phi_m)的逆元
int u = inv(k, phi_m);
cout << "k关于phi(" << m << ")的逆元为: " << u << '\n';
// 求b^u(mod m)
x = binpow(b, u, m);
cout << "x^k=b(mod m)的根为: " << x << '\n';
return 0;
}12——矩阵快速幂



#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
#include <cmath>
typedef long long ll;
using namespace std;
const ll p = 1e9 + 7;
struct mat {
ll c[101][101];
}A, res;
ll n, k;
mat mul(mat& a, mat &b)//矩阵乘法
{
mat t;//临时矩阵
memset(t.c, 0, sizeof(t.c));
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= n; j++)
{
for (int k = 1; k <= n; k++)
{
t.c[i][j] = (t.c[i][j] + a.c[i][k] * b.c[k][j]) % p;
}
}
}
return t;
}
void quickpow(ll k)//快速幂
{
for (int i = 1; i <= n; i++)res.c[i][i] = 1;
while (k)
{
if (k & 1)res = mul(res, A);
A = mul(A, A);
k >>= 1;
}
}
int main()
{
cin >> n >> k;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
cin >> A.c[i][j];
quickpow(k);
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= n; j++)
cout << res.c[i][j] << ' ';
cout << '\n';
}
return 0;
}13——模p平方剩余
14——1-模p平方剩余




 15——2模p平方剩余
15——2模p平方剩余

16——二次互反律
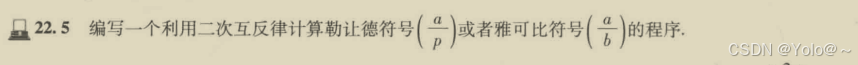































 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








