广度优先搜索（Breadth-First Search，BFS）是一种经典的图遍历算法，广泛应用于最短路径求解、迷宫问题、社交网络分析等领域。本文将深入探讨 BFS 的原理、实现方式及其应用场景，并通过 Java 代码示例进行详细说明。
目录
一、BFS 算法原理
（一）基本思想
BFS 的核心思想是从一个起始节点开始，逐层访问其邻接节点，直到找到目标节点或访问完所有可达节点为止。它按照“先进先出”的原则进行遍历，通常使用队列来实现。
（二）算法流程
-
选择起始节点：从图中的某个节点开始，将其标记为已访问，并加入队列。
-
逐层访问：每次从队列中取出一个节点，访问其所有未访问的邻接节点，并将这些邻接节点标记为已访问，然后加入队列。
-
重复步骤：继续从队列中取出节点，访问其邻接节点，直到队列为空。
（三）迭代实现
BFS 通常使用迭代实现，通过队列来管理待访问的节点。每次从队列中取出一个节点，访问其邻接节点，并将这些邻接节点加入队列。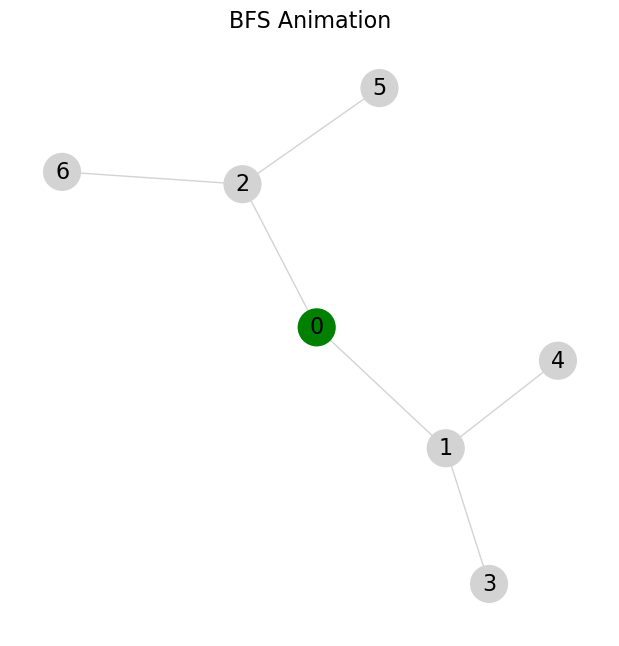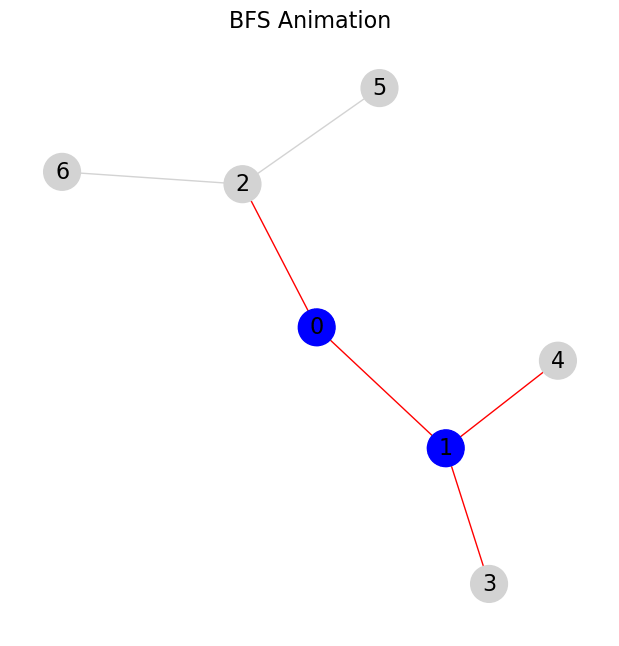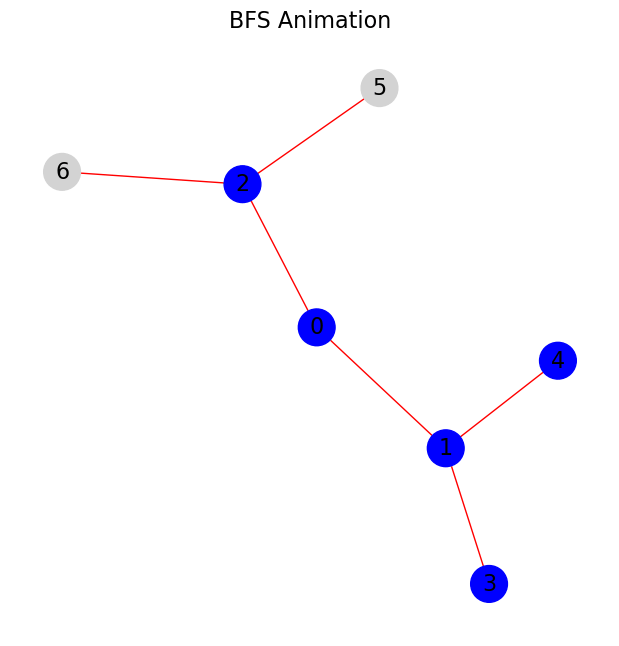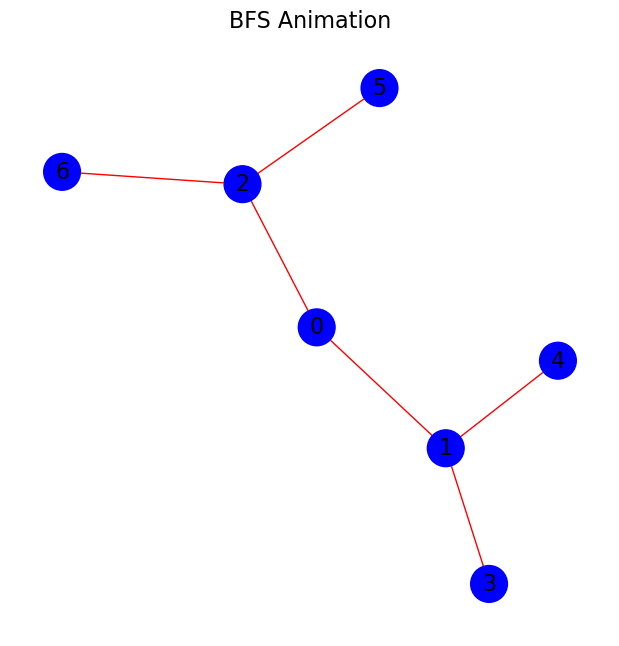
二、BFS 的应用场景
（一）图的遍历
BFS 可以用于遍历图中的所有节点，判断图是否连通。例如，通过 BFS 可以找到图中的所有连通分量。
（二）最短路径求解
BFS 是求解无权图最短路径的经典算法。它能够找到从起点到终点的最短路径，适用于迷宫求解、社交网络中的最短路径等问题。
（三）迷宫问题
在迷宫问题中，BFS 可以用于找到从入口到出口的最短路径。例如，LeetCode 上的题目“1926. 迷宫中离入口最近的出口”就是一个典型的 BFS 应用场景。
三、BFS 的 Java 实现
（一）迭代实现
以下是使用迭代实现 BFS 的 Java 代码示例，代码中添加了详细注释以便理解：
import java.util.*;
// 广度优先搜索（BFS）的迭代实现类
public class BFSIterative {
// visited 数组用于标记节点是否被访问过，防止重复访问
private boolean[] visited;
// graph 是邻接表表示的图，存储每个节点的邻接节点列表
private List<List<Integer>> graph;
// 构造函数，初始化图和访问标记数组
public BFSIterative(int n) {
// 初始化 visited 数组，所有节点初始为未访问
visited = new boolean[n];
// 初始化图的邻接表
graph = new ArrayList<>();
for (int i = 0; i < n; i++) {
// 为每个节点创建一个空的邻接节点列表
graph.add(new ArrayList<>());
}
}
// 添加边的方法，用于构建图
public void addEdge(int u, int v) {
// 无向图：添加 u 到 v 的边，同时添加 v 到 u 的边
// 有向图：只添加 u 到 v 的边
// 此处假设是有向图
graph.get(u).add(v);
}
// BFS 遍历方法
public void bfsTraversal(int start) {
// 使用队列实现 BFS 的迭代过程
Queue<Integer> queue = new LinkedList<>();
// 标记起始节点为已访问
visited[start] = true;
// 将起始节点加入队列
queue.add(start);
// 当队列不为空时，继续遍历
while (!queue.isEmpty()) {
// 从队列中取出一个节点
int node = queue.poll();
// 输出当前节点
System.out.print(node + " ");
// 遍历当前节点的所有邻接节点
for (int neighbor : graph.get(node)) {
// 如果邻接节点未被访问过
if (!visited[neighbor]) {
// 标记为已访问
visited[neighbor] = true;
// 将邻接节点加入队列，以便后续访问其邻接节点
queue.add(neighbor);
}
}
}
}
// 主方法，用于测试 BFS 遍历
public static void main(String[] args) {
// 创建一个包含 6 个节点的图
BFSIterative bfs = new BFSIterative(6);
// 添加边，构建图的结构
bfs.addEdge(0, 1);
bfs.addEdge(0, 2);
bfs.addEdge(1, 3);
bfs.addEdge(2, 4);
bfs.addEdge(3, 5);
bfs.addEdge(4, 5);
// 输出 BFS 遍历的结果
System.out.println("BFS Traversal:");
bfs.bfsTraversal(0);
}
}
四、BFS 应用例题1：迷宫中离入口最近的出口
https://leetcode.cn/problems/nearest-exit-from-entrance-in-maze/solutions/3614228/mi-gong-zhong-chi-ru-kou-zui-jin-de-chu-kvguw（一）问题描述
给定一个迷宫，迷宫由一个二维数组 maze 表示，其中 '.' 表示可以通行的路径，'#' 表示墙壁。从入口出发，找到离入口最近的出口（出口在迷宫的边界上）。返回从入口到最近出口的最短步数，如果无法到达出口，则返回 -1。
（二）BFS 解题思路
BFS 是解决迷宫问题的经典方法。从入口开始，逐层扩展，直到找到一个位于迷宫边界的点，即为最近的出口。
（三）代码实现
以下是使用 BFS 解决“迷宫中离入口最近的出口”问题的 Java 代码示例，代码中每一行都添加了详细注释：
import java.util.*;
public class NearestExitFromEntranceInMaze {
private static final int[] dx = {0, 0, 1, -1};
private static final int[] dy = {1, -1, 0, 0};
public int nearestExit(char[][] maze, int[] entrance) {
int rows = maze.length;
int cols = maze[0].length;
boolean[][] visited = new boolean[rows][cols];
Queue<int[]> queue = new LinkedList<>();
// 从入口开始
queue.add(new int[]{entrance[0], entrance[1]});
visited[entrance[0]][entrance[1]] = true;
int steps = 0;
while (!queue.isEmpty()) {
int size = queue.size();
for (int i = 0; i < size; i++) {
int[] current = queue.poll();
int x = current[0];
int y = current[1];
// 如果当前点不是入口且在边界上，返回步数
if ((x == 0 || x == rows - 1 || y == 0 || y == cols - 1) && (x != entrance[0] || y != entrance[1])) {
return steps;
}
// 遍历四个方向
for (int j = 0; j < 4; j++) {
int newX = x + dx[j];
int newY = y + dy[j];
// 检查是否可以通行且未访问
if (newX >= 0 && newX < rows && newY >= 0 && newY < cols && maze[newX][newY] == '.' && !visited[newX][newY]) {
queue.add(new int[]{newX, newY});
visited[newX][newY] = true;
}
}
}
steps++; // 每扩展一层，步数加1
}
return -1; // 如果无法到达出口，返回-1
}
public static void main(String[] args) {
char[][] maze = {
{'+', '+', '.', '+'},
{'.', '.', '.', '+'},
{'+', '+', '+', '.'}
};
int[] entrance = {1, 2};
NearestExitFromEntranceInMaze solution = new NearestExitFromEntranceInMaze();
System.out.println("Nearest Exit Distance: " + solution.nearestExit(maze, entrance));
}
}（四）代码解析
-
方向数组：
-
dx和dy用于表示上下左右四个方向的移动。
-
-
队列初始化：
-
从入口开始，将入口加入队列，并标记为已访问。
-
-
逐层扩展：
-
每次从队列中取出一个点，检查其是否在边界上且不是入口。如果是，则返回当前步数。
-
否则，遍历其四个方向，将可以通行且未访问的点加入队列，并标记为已访问。
-
-
步数计算：
-
每扩展一层，步数加 1，直到队列为空。
-
（五）复杂度分析
-
时间复杂度：O(m×n)，其中 m 和 n 分别是迷宫的行数和列数。每个单元格最多被访问一次。
-
空间复杂度：O(m×n)，最坏情况下，队列可能包含整个迷宫的节点。
五、BFS 应用2：公交路线
（一）问题描述
给定一个公交路线的列表 routes，其中每个路线是一个整数数组，表示该路线经过的所有站点。同时给定一个起点 source 和终点 target，返回从起点到终点所需的最少换乘次数。如果无法到达终点，则返回 -1。
（二）BFS 解题思路
BFS 是解决此类问题的经典方法。通过将每个公交路线视为一个节点，两个节点之间有边当且仅当它们有共同的站点。从起点所在的路线开始，逐层扩展，直到找到终点所在的路线。
（三）代码实现
以下是使用 BFS 解决“公交路线”问题的 Java 代码示例，代码中每一行都添加了详细注释：
import java.util.*;
public class BusRoutes {
public int numBusesToDestination(int[][] routes, int source, int target) {
if (source == target) {
return 0; // 如果起点和终点相同，无需换乘
}
// 构建站点到路线的映射
Map<Integer, List<Integer>> stationToRoutes = new HashMap<>();
for (int i = 0; i < routes.length; i++) {
for (int station : routes[i]) {
stationToRoutes.putIfAbsent(station, new ArrayList<>());
stationToRoutes.get(station).add(i);
}
}
// BFS 初始化
Queue<Integer> queue = new LinkedList<>();
Set<Integer> visitedRoutes = new HashSet<>();
Set<Integer> visitedStations = new HashSet<>();
// 从起点出发
queue.add(source);
visitedStations.add(source);
int transfers = 0;
while (!queue.isEmpty()) {
int size = queue.size();
for (int i = 0; i < size; i++) {
int currentStation = queue.poll();
// 遍历当前站点的所有路线
for (int route : stationToRoutes.getOrDefault(currentStation, Collections.emptyList())) {
if (visitedRoutes.contains(route)) {
continue; // 如果该路线已经访问过，跳过
}
visitedRoutes.add(route);
// 遍历该路线上的所有站点
for (int nextStation : routes[route]) {
if (nextStation == target) {
return transfers + 1; // 找到终点，返回换乘次数
}
if (!visitedStations.contains(nextStation)) {
queue.add(nextStation);
visitedStations.add(nextStation);
}
}
}
}
transfers++; // 每扩展一层，换乘次数加1
}
return -1; // 如果无法到达终点，返回-1
}
public static void main(String[] args) {
int[][] routes = {
{1, 2, 7},
{3, 6, 7}
};
int source = 1;
int target = 6;
BusRoutes solution = new BusRoutes();
System.out.println("Minimum Transfers: " + solution.numBusesToDestination(routes, source, target));
}
}（四）代码解析
-
站点到路线的映射：
-
使用
stationToRoutes将每个站点映射到它所在的路线。这样可以快速找到从一个站点出发可以到达的所有路线。
-
-
BFS 初始化：
-
使用队列
queue存储当前访问的站点。 -
使用
visitedRoutes和visitedStations分别记录已经访问过的路线和站点，避免重复访问。
-
-
逐层扩展：
-
每次从队列中取出一个站点，找到该站点可以到达的所有路线。
-
对于每条路线，遍历其上的所有站点，如果找到终点则返回当前换乘次数。
-
将未访问过的站点加入队列，并标记为已访问。
-
-
换乘次数计算：
-
每扩展一层，换乘次数加 1，直到队列为空。
-
（五）复杂度分析
-
时间复杂度：O(N + S)，其中 N 是路线的数量，S 是所有站点的总数。每个站点和路线最多被访问一次。
-
空间复杂度：O(N + S)，用于存储站点到路线的映射以及访问记录。
六、BFS 的优缺点
（一）优点
-
保证最短路径：BFS 能够找到无权图中的最短路径。
-
实现简单：迭代实现的代码简洁明了。
-
适用于大规模数据：对于大规模图或树结构，BFS 可以有效地找到目标。
（二）缺点
-
空间复杂度高：在稠密图中，队列可能会占用大量空间。
-
效率较低：在某些情况下，BFS 的时间复杂度可能较高。
六、总结
广度优先搜索（BFS）是一种重要的图遍历算法，具有广泛的应用场景。通过迭代实现，BFS 可以有效地探索图中的所有节点。在竞赛中，BFS 也常用于解决迷宫问题，如“迷宫中离入口最近的出口”问题。希望本文对大家学习和理解广度优先搜索算法有所帮助。如果有任何问题或建议，欢迎在评论区留言。
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
