Day16------2025.4.23
D. Swap Dilemma(贪心模拟)
思路
感觉此题有坑啊刚开始以为是有结论的类似于并查集相互对应结果交了一发WA2了
之后尝试贪心发现我们需要固定一个数组不变,只需要贪心地让另一个数组逐渐和固定数组相等即可,怎么固定不变并且还能够将另一数组改变呢?这得益于题面的操作方法
假设固定a数组,我们对a进行操作|(1 3)(3 1)是不是没有变化,而对b进行操作(3 5) (1 3),我们就将原本处于5位置的数移到了1位置而a数组的数并没有发生改变
接下来直接贪心模拟即可
代码
#include<bits/stdc++.h>
using namespace std;
#define vcoistnt ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
#define int long long
#define vi vector<int>
#define vb vector<bool>
typedef pair<int,int> pll;
const int N=2e5+10;
const int inf=1e18;
const int mod=998244353;
void solve(){
int n;cin>>n;
vi a(n+10),b(n+10);
for(int i=1;i<=n;i++) cin>>a[i];
for(int i=1;i<=n;i++) cin>>b[i];
//最初特判
vi ta=a,tb=b;
sort(ta.begin()+1,ta.begin()+1+n);
sort(tb.begin()+1,tb.begin()+1+n);
if(ta!=tb){
cout<<"NO\n";return;
}
map<int,int> pos; //记录数x在b中的位置
for(int i=1;i<=n;i++) pos[b[i]]=i;
for(int i=1;i<=n;i++){ //开始模拟贪心交换过程
if(a[i]==b[i]) continue;
int id=pos[a[i]];
bool f=false;
if((id-i)%2) f=true;
int siz=(id-i)/2;
if(f){
pos[b[id]]=i;
pos[b[id-siz]]=id;
pos[b[id-siz-siz]]=id-siz;
pos[b[i]]=i+1;
swap(b[id],b[id-siz]);
swap(b[id-siz],b[id-siz-siz]);
swap(b[id-siz-siz],b[i]);
pos[b[n-1]]=n;
pos[b[n]]=n-1;
swap(b[n],b[n-1]);
}else{
pos[b[id]]=i;
pos[b[id-siz]]=id;
pos[b[i]]=id-siz;
swap(b[id],b[id-siz]);
swap(b[i],b[id-siz]);
}
}
for(int i=1;i<=n;i++){
if(a[i]!=b[i]){
cout<<"NO\n";return;
}
}
cout<<"YES\n";
}
signed main() {
vcoistnt
cout<<fixed<<setprecision(2);
int _=1;
cin>>_;
while(_--) solve();
return 0;
}G. Chimpanzini Bananini(模拟+数学)
思路
思路倒是很简单,我们只需要在O(1)的复杂度下更新操作完成后的答案
对于操作3,我们只是在后面加入k元素所以答案更新:
对于操作1,我们将最后一个数移到前面,将其余的数往后移一位,最后的数对答案的贡献为其余数的贡献其实是在每个数又加了一遍
,我们用sum来维护所有元素的总和
答案更新:
对于操作2,我们将数组反转根据一些观察我们发现反转后的ans+反转前的ans的值是固定的即对两个数列的加和提取公因数的结果,那么答案更新:
那么答案更新明确了之后我们便开始维护需要维护的值:ans,sum,n,a[n]
对于最后一个数a[n]的维护我们可以用双端队列
代码
#include<bits/stdc++.h>
using namespace std;
#define vcoistnt ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
#define int long long
#define vi vector<int>
#define vb vector<bool>
typedef pair<int,int> pll;
const int N=2e5+10;
const int inf=1e18;
const int mod=998244353;
void solve(){
int q;
cin>>q;
deque<int> dq;
int ans=0; //记录*i的和
int sum=0; //记录元素和
int n=0; //记录元素个数
int x=0; //记录当前数组的最后一个元素值
bool f=false; //false表示我们从后面取数,true表示从前面取数
while(q--){
int s;cin>>s;
if(s==1){
if(f){
x=dq.front(); dq.pop_front();
ans=(ans-x*n)+sum;
dq.push_back(x);
}else{
x=dq.back(); dq.pop_back();
ans=ans-x*n+sum;
dq.push_front(x);
}
}else if(s==2){
ans=sum*(n+1)-ans;
f=!f;
}else if(s==3){
int k;cin>>k;
sum+=k;
++n;
ans+=k*n;
if(!f) dq.push_back(k);
else dq.push_front(k);
}
cout<<ans<<"\n";
}
}
signed main() {
vcoistnt
cout<<fixed<<setprecision(2);
int _=1;
cin>>_;
while(_--) solve();
return 0;
}Day15------2025.4.16
E. Beautiful Array(贪心数学)
思路
我们发现两个数进行操作之后能变成相等的数时那么这两个数%k是相等的,那么我们便把%k相等的数放在一起,方便统计操作我们只需要将(a[i]/k)放到序列里面,排序之后相邻两数的差便是最小的操作,对于偶数来说是直接求,对于奇数来说我们需要将一个数放到中间,如果直接枚举的话会T,我们需要用前缀和后缀和优化
代码
#include<bits/stdc++.h>
using namespace std;
#define vcoistnt ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
#define int long long
#define vi vector<int>
#define vb vector<bool>
typedef pair<int,int> pll;
const int N=2e5+10;
const int inf=1e18;
const int mod=998244353;
void solve(){
int n,k;
cin>>n>>k;
vi a(n+10);
for(int i=1;i<=n;i++){
cin>>a[i];
}
map<int,bool> mp; //记录余数为x是否出现
int cnt=0; //统计余数的数量如果大于n/2就直接输出-1,防止内存爆掉
vector<vi> v(n+10); //在余数为i=id[x]的情况下k的情况
int ct=0; //将余数的情况离散化一下
map<int,int> id;
for(int i=1;i<=n;i++){
if(!mp[a[i]%k]){
cnt++;
mp[a[i]%k]=true;
}
if(cnt>(n+1)/2){
cout<<"-1\n";return;
}
if(!id[a[i]%k]){
id[a[i]%k]=++ct;
}
v[id[a[i]%k]].push_back(a[i]/k);
}
int t=0;
for(int i=1;i<=ct;i++){
if(v[i].size()%2) t++;
}
if(t>1){ //n为奇数时至少会有一个,n为偶数时只要有一个必然会是两个,所以只需要判t>1即可
cout<<"-1\n";return;
}
int ans=0;
if(n%2==0){ //处理偶数时直接排序之后相邻两数做差即可
for(int i=1;i<=n;i++){
sort(v[i].begin(),v[i].end());
for(int j=0;j<v[i].size();j+=2){
ans+=(v[i][j+1]-v[i][j]);
}
}
}else{ //处理奇数我们把奇数单独拿出来计算
vi vodd;
int nt=0;
for(int i=1;i<=n;i++){
sort(v[i].begin(),v[i].end());
if(v[i].size()%2){
nt=v[i].size();
vodd=v[i];continue;
}
for(int j=0;j<v[i].size();j+=2){
ans+=(v[i][j+1]-v[i][j]);
}
}
vi pre(nt/2+10,0),suf(nt/2+10,0);
int tid=0;
for(int i=0;i<nt-1;i+=2){
tid++;
pre[tid]=pre[tid-1]+(vodd[i+1]-vodd[i]);
}
int sid=nt/2+1;
for(int i=nt-1;i>0;i-=2){
sid--;
suf[sid]=suf[sid+1]+(vodd[i]-vodd[i-1]);
}
int mx=inf;
for(int i=0;i<=tid;i++){
mx=min(mx,pre[i]+suf[i+1]);
}
ans+=mx;
}
cout<<ans<<"\n";
}
signed main() {
vcoistnt
cout<<fixed<<setprecision(2);
int _=1;
cin>>_;
while(_--) solve();
return 0;
}Day14------2025.4.15
G. D-Function(数学)
思路
D(k*n)=k*D(n),观察发现只有在所有位x*k的不进位的情况下此等式才会成立。
如k=4,n=303时,D(1212)=6 4*D(303)=24
如果k乘以n的某一位之后发生了进位那么贡献便会改变,然后发现只有在k<10的情况下才有可能成立
然后用数学来统计答案,如且
,我们对于数字的选择只有0 1 2
1000-9999 我们除了开头的位数只能选1 2,其余位数选0 1 2,答案便是2*3*3*3
10000-99999答案2*3*3*3*3
累加起来,我们发现是个等比数列求和首项、公比、项数都知道了直接公式求即可
代码
#include<bits/stdc++.h>
using namespace std;
#define vcoistnt ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
#define int long long
#define vi vector<int>
#define vb vector<bool>
typedef pair<int,int> pll;
const int N=2e5+10;
const int inf=1e18;
const int mod=1e9+7;
int ksm(int a,int b){
int ans=1;
while(b){
if(b&1){
ans=(ans*a)%mod;
}
a=((a%mod)*(a%mod))%mod;
b>>=1;
}
return ans;
}
int inverse(int x){
return ksm(x,mod-2)%mod;
}
vector<int> cnt(11);
void solve(){
int l,r,k;cin>>l>>r>>k;
if(k>=10){
cout<<"0\n";return;
}
int a1=(ksm(cnt[k],l)*(cnt[k]-1))%mod;
int q=cnt[k];
int n=r-l;
cout<<(a1*(ksm(q,n)-1)%mod)*inverse(q-1)%mod<<"\n";
}
signed main() {
vcoistnt
cout<<fixed<<setprecision(2);
cnt[1]=10;cnt[2]=5;cnt[3]=4;cnt[4]=3;cnt[5]=2;
cnt[6]=2;cnt[7]=2;cnt[8]=2;cnt[9]=2;
int _=1;
cin>>_;
while(_--) solve();
return 0;
}B2. Bouquet (Hard Version)(贪心)
思路
此题贪心,直接看代码,已经做了详细注释
代码
#include<bits/stdc++.h>
using namespace std;
#define vcoistnt ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
#define int long long
#define vi vector<int>
#define vb vector<bool>
typedef pair<int,int> pll;
const int N=2e5+10;
const int inf=1e18;
const int mod=998244353;
struct node{
int a,c;
};
bool cmp(node x,node y){
return x.a<y.a;
}
void solve(){
int n,m;cin>>n>>m;
vector<node> st(n+10);
for(int i=1;i<=n;i++){
cin>>st[i].a;
}
for(int i=1;i<=n;i++){
cin>>st[i].c;
}
sort(st.begin()+1,st.begin()+1+n,cmp);
int ans=0;
for(int i=1;i<=n;i++){
//选择两种花的情况
if(i!=n&&st[i+1].a-st[i].a==1){
if(st[i].a*st[i].c+st[i+1].a*st[i+1].c<=m){ //如果两种花都选了还<=m直接更新ans
ans=max(ans,(st[i].a*st[i].c+st[i+1].a*st[i+1].c));
}else{
if(st[i].a*st[i].c<m){
//贪心 先将所有的第一组花填上再尝试填第二组花,之后再尝试用剩下的第二组花替换第一种花
int x=st[i].a*st[i].c;
int res=m-x;
int t=res/st[i+1].a;
int ct=st[i+1].c-t;
res-=t*st[i+1].a;
ct=min(ct,st[i].c); //记录能够被替换的第一组花
ans=max(ans,min(m,st[i].a*st[i].c+st[i+1].a*t+ct));
}else{
//把第一种花填满直到大于m,用第二种花去替换
int t=m/st[i].a;
int res=m-st[i].a*t;
int ct=min(t,st[i+1].c);
ans=max(ans,min(m,st[i].a*t+ct));
}
}
}
//只选择一种花
int t=min(st[i].c,m/st[i].a);
ans=max(ans,st[i].a*t);
}
cout<<ans<<"\n";
}
signed main() {
vcoistnt
cout<<fixed<<setprecision(2);
int _=1;
cin>>_;
while(_--) solve();
return 0;
}E. Look Back
思路
首先尝试暴力,即遇到a[i]<a[i-1]将a[i]*2一直到大于等于为止,发现时间复杂度过高,那么我们只能换一种思路
经过转化之后的数组我们看成对于任意两相邻的数
那么x与y是否存在某种联系呢?
我们发现当a1>a2时y与x的差值便是让a2一直*2直到大于等于a1的次数
那么我们直接算出这个次数最后累加即可
代码
#include<bits/stdc++.h>
using namespace std;
#define vcoistnt ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
#define int long long
#define vi vector<int>
#define vb vector<bool>
typedef pair<int,int> pll;
const int N=2e5+10;
const int inf=1e18;
const int mod=998244353;
void solve(){
int n;
cin>>n;
vi a(n+10);
for(int i=1;i<=n;i++){
cin>>a[i];
}
vi op(n+10);
for(int i=2;i<=n;i++){
int him=a[i-1];
int me=a[i];
int extra=0;
while(him*2<=me){
extra--;
him*=2;
}
while(me<him){
extra++;
me*=2;
}
op[i]=max(0ll,op[i-1]+extra);
}
int ans=0;
for(int i=1;i<=n;i++) ans+=op[i];
cout<<ans<<"\n";
}
signed main() {
vcoistnt
cout<<fixed<<setprecision(2);
int _=1;
cin>>_;
while(_--) solve();
return 0;
}C. Squaring
思路
与上一题一样,只是将*2换成了^2
代码
#include<bits/stdc++.h>
using namespace std;
#define vcoistnt ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
#define int long long
#define vi vector<int>
#define vb vector<bool>
typedef pair<int,int> pll;
const int N=2e5+10;
const int inf=1e18;
const int mod=998244353;
void solve(){
int n;
cin>>n;
vi a(n+10);
for(int i=1;i<=n;i++){
cin>>a[i];
}
for(int i=2;i<=n;i++){
if(a[i]==1&&a[i]<a[i-1]){
cout<<"-1\n";return;
}
}
vi op(n+10);
for(int i=2;i<=n;i++){
int him=a[i-1];
int me=a[i];
int extra=0;
while(him!=1&&him*him<=me){
extra--;
him*=him;
}
while(me<him){
extra++;
me*=me;
}
op[i]=max(0ll,op[i-1]+extra);
}
int ans=0;
for(int i=1;i<=n;i++) ans+=op[i];
cout<<ans<<"\n";
}
signed main() {
vcoistnt
cout<<fixed<<setprecision(2);
int _=1;
cin>>_;
while(_--) solve();
return 0;
}Day13------2025.4.14
C. Lazy Narek(动态规划)
思路
根据经验来谈,此题是一个动态规划的题
因为是拼接我们秉持着当加入一个字符串时对于此字符串肯定是能匹配便匹配的原则这样便是最优的
我们发现当加入字符串的时候我们匹配的情况是与前面的字符串最后一组匹配剩下的字符有关的,我们于是我们设表示前 i 个字符随意组合,最后一组剩下的字符数量为 j 时的最大可能分数
对于每个要加入的字符串我们令表示当前面已经匹配了j个字符时,加入此字符串最后一组匹配剩下的字符数量,
表示前面已经匹配了j个字符时,加入此字符串能够得到的分数
所以状态转移方程便是
最后答案便是
-j的原因是在计算sum时我们会将最后一组匹配的字符数量算入到sorce_n里
注:可以用滚动数组实现来优化空间
代码
#include<bits/stdc++.h>
using namespace std;
#define vcoistnt ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
#define int long long
#define vi vector<int>
#define vb vector<bool>
typedef pair<int,int> pll;
const int N=2e5+10;
const int inf=1e18;
const int mod=998244353;
map<char,int> mp;
void solve(){
int n,m;
cin>>n>>m;
vector<string> s(n+10);
for(int i=1;i<=n;i++){
cin>>s[i];
s[i]=" "+s[i];
}
vector<vector<int>> dp(n+10,vi(6,-inf));
dp[0][0]=0;
for(int i=1;i<=n;i++){
vector<int> len(6,0),sum(6,0);
for(int j=0;j<=4;j++){ //初始化len如果此字符串没有匹配进任何字符,那么最后一组匹配的字符还是j
len[j]=j;
}
for(int j=1;j<=m;j++){
if(mp[s[i][j]]){ //此字符是narek中的一种,我们就需要更新len以及sum
for(int k=0;k<=4;k++){
if(mp[s[i][j]]==len[k]+1){
len[k]++;
if(len[k]==5){
sum[k]+=5;
len[k]=0;
}
}else{
sum[k]--;
}
}
}
}
for(int j=0;j<=4;j++){ //如果当前的字符串不加入直接继承
dp[i][j]=dp[i-1][j];
}
for(int j=0;j<=4;j++){
dp[i][len[j]]=max(dp[i][len[j]],dp[i-1][j]+sum[j]);
}
}
int ans=0;
for(int i=0;i<=4;i++) ans=max(ans,dp[n][i]-i); //-i是在计算sum时我们将最后j个字符算入了socore_n里面
cout<<ans<<"\n";
}
signed main() {
vcoistnt
cout<<fixed<<setprecision(2);
mp['n']=1;mp['a']=2;mp['r']=3;mp['e']=4;mp['k']=5;
int _=1;
cin>>_;
while(_--) solve();
return 0;
}Day12------2025.4.13
E. Rendez-vous de Marian et Robin(最短路)
思路
最短路的题,在原有的最短路添加了有马可以距离减半的条件
求1到各个顶点的最短距离,求n到各个顶点的最短距离,遍历所有顶点统计答案即可
我们可以对dis距离数组开个二维,分别表示没有马时到x的距离,以及有马时到x的距离即可
代码
#include<bits/stdc++.h>
using namespace std;
#define vcoistnt ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
#define int long long
#define vi vector<int>
#define vb vector<bool>
typedef pair<int,int> pll;
const int N=2e5+10;
const int inf=1e18;
const int mod=998244353;
struct cmp{
bool operator()(const array<int,3> &a,const array<int,3> &b){
return a[0]>b[0];
}
};
void solve(){
int n,m,h;
cin>>n>>m>>h;
vi horse(n+10); //记录有马的节点
for(int i=1;i<=h;i++){
int x;cin>>x;
horse[x]=1;
}
vector<vector<pll>> edge(n+10);
for(int i=1;i<=m;i++){
int u,v,w;cin>>u>>v>>w;
edge[u].push_back({v,w});
edge[v].push_back({u,w});
}
auto Dij=[&](int s,vector<vector<int>>&dis)->void{
priority_queue<array<int,3>,vector< array<int,3> >,cmp> q; //距离,节点,有没有马
vector<vector<int>> vis(n+10,vi(2));
dis[s][horse[s]]=0;
q.push({0,s,horse[s]});
while(!q.empty()){
auto [len,u,op]=q.top();
q.pop();
if(vis[u][op]) continue;
vis[u][op]=1;
for(auto [v,w]:edge[u]){
int now = (op ? 1:horse[u]);
if(dis[v][now]>dis[u][op]+(now?w/2:w)){
dis[v][now]=dis[u][op]+(now?w/2:w);
if(!vis[v][now]){
q.push({dis[v][now],v,now});
}
}
}
}
};
vector<vi> d1(n+10,vi(2,inf)); //d1[i][0]表示到i节点没有马的距离 1表示有马
vector<vi> d2(n+10,vi(2,inf));
Dij(1,d1); Dij(n,d2);
int ans=inf;
for(int i=1;i<=n;i++){
if((d1[i][0]==inf&&d1[i][1]==inf)||(d2[i][0]==inf&&d2[i][1]==inf)) continue;
int dis1=min(d1[i][0],d1[i][1]);
int dis2=min(d2[i][0],d2[i][1]);
ans=min(ans,max(dis1,dis2));
}
if(ans==inf){
cout<<"-1\n";return;
}
cout<<ans<<"\n";
}
signed main() {
vcoistnt
cout<<fixed<<setprecision(2);
int _=1;
cin>>_;
while(_--) solve();
return 0;
}G. Sakurako's Task(数学)
思路
很容易发现如果数列中出现了1,那么我们可以把数转化成0 1 2 3....但是对于样例
2 2 2 16
中未出现1时该怎么得到最优,我们发现最后转换成0 2 4 6是最优的
对于两个数来说我们要得到这两个数所转换的最小且不为零的数,然后用这个数来转换其他的数,那么我们的任务就变成了寻找数列在转换过程中得到的最小不为零的数,然后用这个数来构建最优序列,即0 x 2*x 3*x ....
那么怎么转换的呢?对于 5 17来说,我们先把17->2,再用2使5->1,便得到了最小数1
然后发现这不就是求gcd的辗转相除法吗?
代码
#include<bits/stdc++.h>
using namespace std;
#define vcoistnt ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
#define int long long
#define vi vector<int>
#define vb vector<bool>
typedef pair<int,int> pll;
const int N=2e5+10;
const int inf=1e18;
const int mod=998244353;
void solve(){
int n,k;
cin>>n>>k;
vi a(n+10);
for(int i=1;i<=n;i++){
cin>>a[i];
}
if(n==1){
if(a[1]>=k){
cout<<k-1<<"\n";
}else{
cout<<k<<"\n";
}
return;
}
int x=0;
for(int i=1;i<=n;i++){
x=__gcd(x,a[i]);
}
if(x==1){
cout<<n-1+k<<"\n";return;
}
cout<<min((k-1)/(x-1),n-1)+k<<"\n";
}
signed main() {
vcoistnt
cout<<fixed<<setprecision(2);
int _=1;
cin>>_;
while(_--) solve();
return 0;
}Day11------2025.4.8
C. Hungry Games(dp动态规划)
思路
根据题意我们很容易发觉是个动态规划的题目,做两个尝试
1.设dp[i]为以i位置为结尾的合法区间数量,发现行不通,状态转移方程难想
2.设dp[i]表示以i位置为开头的合法区间数量,我们发现只要当前累加和大于x后将其变为0,我们就能拿以此位置之后为开头来更新此dp值
那么状态转移方程便明确了,从后往前遍历更新
当
当
其中p是第一个从i到p位置累加和大于x的位置,p-i是长度
找p的时候需要用前缀和二分来优化一下,来降低复杂度
代码
#include<bits/stdc++.h>
using namespace std;
#define vcoistnt ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
#define int long long
#define vi vector<int>
#define vb vector<bool>
typedef pair<int,int> pll;
const int N=2e5+10;
const int inf=1e18;
const int mod=998244353;
void solve(){
int n,x;
cin>>n>>x;
vi a(n+10);
vi pre(n+1);
for(int i=1;i<=n;i++){
cin>>a[i];
pre[i]=pre[i-1]+a[i];
}
vi dp(n+10,0);
for(int i=n;i>=1;i--){
if(a[i]>x){
dp[i]=dp[i+1];
}else{
int p=upper_bound(pre.begin()+i,pre.begin()+1+n,pre[i-1]+x)-pre.begin();
dp[i]=dp[p+1]+p-i;
}
}
int ans=0;
for(int i=1;i<=n;i++){
ans+=dp[i];
}
cout<<ans<<"\n";
}
signed main() {
vcoistnt
cout<<fixed<<setprecision(2);
int _=1;
cin>>_;
while(_--) solve();
return 0;
}C. Job Interview(贪心模拟)
思路
感觉此题比较偏逻辑,感觉没1600的难度
来到i位置时,如果此人去了a岗位,那么我们删掉之后肯定是将第一个要去a岗位但去了b岗位的人弄到a岗位去,然后b岗位又会空出一个,那么第一个要去b岗位但去了a岗位的人去b岗位即可
反之亦然
要注意最后一个人要单独拿出来
但后来发现并没有那么麻烦。。。因为n和m必然有一个先到达0,那么之后的人便都会去另一个岗位
代码
#include<bits/stdc++.h>
using namespace std;
#define vcoistnt ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
#define int long long
#define vi vector<int>
#define vb vector<bool>
typedef pair<int,int> pll;
const int N=2e5+10;
const int inf=1e18;
const int mod=998244353;
void solve(){
int n,m;
cin>>n>>m;
vi a(n+m+10);
vi b(n+m+10);
for(int i=1;i<=n+m+1;i++){
cin>>a[i];
}
for(int i=1;i<=n+m+1;i++){
cin>>b[i];
}
int tn=n,tm=m;
vi x,y;
//x存想去a岗位但名额满了去了b岗位
//y存想去b岗位但名额满了去了a岗位
int sum=0;
map<int,int> idx;
map<int,int> idy;
for(int i=1;i<=n+m;i++){
if(a[i]>b[i]){
if(tn>0){
tn--;
sum+=a[i];
}else{
tm--;
sum+=b[i];
x.push_back(i);
idx[i]=x.size();
}
}else{
if(tm>0){
tm--;
sum+=b[i];
}else{
tn--;
sum+=a[i];
y.push_back(i);
idy[i]=y.size();
}
}
}
for(int i=1;i<=n+m;i++){
int res=sum;
if(!idx[i]&&!idy[i]){ //表示此编号如愿以偿的得到了能力大的职位
if(a[i]>b[i]){
res-=a[i];
if(x.size()){
res-=b[x[0]];
res+=a[x[0]];
if(y.size()){
res-=a[y[0]];
res+=b[y[0]];
}else{
res+=b[n+m+1];
}
}else{
res+=a[n+m+1];
}
}else{
res-=b[i];
if(y.size()){
res-=a[y[0]];
res+=b[y[0]];
if(x.size()){
res-=b[x[0]];
res+=a[x[0]];
}else{
res+=a[n+m+1];
}
}else{
res+=b[n+m+1];
}
}
}else if(idx[i]){
res-=b[i];
if(y.size()){
res-=a[y[0]];
res+=b[y[0]];
if(x.size()){
res-=b[x[0]];
res+=a[x[0]];
}else{
res+=a[n+m+1];
}
}else{
res+=b[n+m+1];
}
}else{
res-=a[i];
if(x.size()){
res-=b[x[0]];
res+=a[x[0]];
if(y.size()){
res-=a[y[0]];
res+=b[y[0]];
}else{
res+=b[n+m+1];
}
}else{
res+=a[n+m+1];
}
}
cout<<res<<" ";
}
cout<<sum<<"\n";
}
signed main() {
vcoistnt
cout<<fixed<<setprecision(2);
int _=1;
cin>>_;
while(_--) solve();
return 0;
}Day10------2025.4.7
D. Minimize the Difference(贪心)
思路
观察发现两个点:
1.我们要尽可能地贪心将数变成平均值,然后就能最小化答案
2.限制条件是前面的数能够将值传给后面,后面的值不能传给前面
那么我们便从1-n开始贪心,当加入的值小于平均值,我们重新维护平均值使得所有数都接近平均值,如果大于当前的平均值,因为我们无法将后面的值传给前面,那么我们便以此数为开头再维护一个区间的平均值
我们可以用一个栈来实现,{x,cnt}表示值为x的数有cnt个
代码
#include<bits/stdc++.h>
using namespace std;
#define vcoistnt ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
#define int long long
#define vi vector<int>
#define vb vector<bool>
typedef pair<int,int> pll;
const int N=2e5+10;
const int inf=1e18;
const int mod=998244353;
void solve(){
int n;cin>>n;
vector<int> a(n+10);
for(int i=1;i<=n;i++){
cin>>a[i];
}
stack<pll> s;
for(int i=1;i<=n;i++){
int sum=a[i],cnt=1;
while(s.size() && s.top().first>=sum/cnt){
sum += s.top().first*s.top().second;
cnt += s.top().second;
s.pop();
}
s.push({sum/cnt,cnt-sum%cnt});
if(sum%cnt!=0){
s.push({sum/cnt+1,sum%cnt});
}
}
int mx=s.top().first;
while(s.size()>1){
s.pop();
}
cout<<mx-s.top().first<<"\n";
}
signed main() {
vcoistnt
cout<<fixed<<setprecision(2);
int _=1;
cin>>_;
while(_--) solve();
return 0;
}E. Decode(前缀和+组合数学)
思路
我们发现要求01数量相等的区间,我们不妨将0设置为-1,1设置为+1,那么就是求区间和为0的部分,放在前缀和中就是出现相同数的区间
假设(x,y)区间01数量相同,那么有多少个(l,r)区间包含(x,y)?
结果显然是(x)*(n-y+1)那么此问题便得到了转换,每遇到一个区间内01数量相同便更新答案,那么这么贪心是否正确?大区间是否被小区间覆盖,发现是正确的
代码
#include<bits/stdc++.h>
using namespace std;
#define vcoistnt ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
#define int long long
#define vi vector<int>
#define vb vector<bool>
typedef pair<int,int> pll;
const int N=2e5+10;
const int inf=1e18;
const int mod=1e9+7;
void solve(){
string s;
cin>>s;
int n=s.size();
s=" "+s;
map<int,int> mp;
int sum=0;
int cnt=0;
mp[0]=1;
for(int i=1;i<=n;i++){
if(s[i]=='1') sum++;
else sum--;
cnt=(cnt+mp[sum]*(n-i+1))%mod;
mp[sum]=(mp[sum]+(i+1))%mod;
}
cout<<cnt<<"\n";
}
signed main() {
vcoistnt
cout<<fixed<<setprecision(2);
int _=1;
cin>>_;
while(_--) solve();
return 0;
}Day9------2025.4.2
D. Cyclic MEX(数据结构双端队列+模拟过程 或者用吉司机线段树做)
思路
首先思路明确便是枚举一遍 将 i 作为开头时求一遍mex和,尝试以或
的复杂度解决求和问题
我们可以试着模拟一遍过程,发现每次我们将移到后面时势必会将所有mex>p[i]的值变成p[i],再在最后插入一个n
那么现在想必学过吉司机线段树的就能想到这不就是板子题吗,将所有区间然后将p[i]的mex值变为n,然后求和,当然这题对写代码来说很有挑战性,有卡常的风险,能过也是很极限了,有个技巧就是开2*n的线段树
显然这题还有另一种做法,那就是用双端队列模拟,我们需要状态压缩一下,也就是将mex值相等的数压缩之后放到队列里面,之后再逐渐模拟
代码
吉司机线段树
#include<bits/stdc++.h>
using namespace std;
#define vcoistnt ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
#define int long long
#define vi vector<int>
#define vb vector<bool>
typedef pair<int,int> pll;
const int N=1e6+10;
const int inf=1e18;
const int mod=998244353;
const int LOWEST=-1; //定义比最小值还小
const int MAXN=1000001;
struct SegmentTreeminQueryMaxsum{
vector<int> sum,mx,cnt,sem;
SegmentTreeminQueryMaxsum(int n):sum(4*n),mx(4*n),cnt(4*n),sem(4*n){}
void up(int i){
int l=i << 1;
int r=i << 1 | 1;
sum[i]=sum[l]+sum[r];
mx[i]=max(mx[l],mx[r]);
if(mx[l]>mx[r]){
cnt[i]=cnt[l];
sem[i]=max(sem[l],mx[r]);
}else if(mx[l]<mx[r]){
cnt[i]=cnt[r];
sem[i]=max(mx[l],sem[r]);
}else{
cnt[i]=cnt[l]+cnt[r];
sem[i]=max(sem[l],sem[r]);
}
}
void down(int i){
lazy(i<<1,mx[i]);
lazy(i<<1|1,mx[i]);
}
//一定是没有覆盖掉次大值的懒更新信息下发
void lazy(int i,int v){
if(v<mx[i]){
sum[i]-=(mx[i]-v)*cnt[i];
mx[i]=v;
}
}
void build(int l,int r,int i){
if(l==r){
sum[i]=mx[i]=1e9;
cnt[i]=1;
sem[i]=LOWEST;
}else{
int mid=(l+r)>>1;
build(l,mid,i<<1);
build(mid+1,r,i<<1|1);
up(i);
}
}
void setMin(int jobl,int jobr,int jobv,int l,int r,int i){
if(jobv>=mx[i]){
return;
}
if(jobl<=l&&r<=jobr&&sem[i]<jobv){
lazy(i,jobv);
}else{
down(i);
int mid=(l+r)>>1;
if(jobl<=mid){
setMin(jobl,jobr,jobv,l,mid,i<<1);
}
if(jobr>mid){
setMin(jobl,jobr,jobv,mid+1,r,i<<1|1);
}
up(i);
}
}
int queryMax(int jobl,int jobr,int l,int r,int i){
if(jobl<=l&&r<=jobr){
return mx[i];
}
down(i);
int mid=(l+r)>>1;
int ans=INT_MIN;
if(jobl<=mid){
ans=max(ans,queryMax(jobl,jobr,l,mid,i<<1));
}
if(jobr>mid){
ans=max(ans,queryMax(jobl,jobr,mid+1,r,i<<1|1));
}
return ans;
}
int querySum(int jobl,int jobr,int l,int r,int i){
if(jobl<=l&&r<=jobr){
return sum[i];
}
down(i);
int mid=(l+r)>>1;
int ans=0;
if(jobl<=mid){
ans+=querySum(jobl,jobr,l,mid,i<<1);
}
if(jobr>mid){
ans+=querySum(jobl,jobr,mid+1,r,i<<1|1);
}
return ans;
}
};
void solve(){
int n;cin>>n;
vi p(n+10);
for(int i=1;i<=n;i++){
cin>>p[i];
}
SegmentTreeminQueryMaxsum st(2*n);
st.build(1,2*n,1);
vector<int> mp(n+1);
int mex=0;
for(int i=1;i<=n;i++){
mp[p[i]]=true;
while(mp[mex]){
mex++;
}
st.setMin(i,i,mex,1,2*n,1);
}
int ans=st.querySum(1,n,1,2*n,1);
for(int i=2;i<=n;i++){
int r=i+n-1;
st.setMin(i-1,i-1,0,1,2*n,1);
st.setMin(i,r-1,p[i-1],1,2*n,1);
st.setMin(r,r,n,1,2*n,1);
ans=max(ans,st.querySum(1,r,1,2*n,1));
}
cout<<ans<<"\n";
}
signed main() {
vcoistnt
cout<<fixed<<setprecision(2);
int _=1;
cin>>_;
while(_--) solve();
return 0;
}双端队列模拟做法
#include<bits/stdc++.h>
using namespace std;
#define vcoistnt ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
#define int long long
#define vi vector<int>
#define vb vector<bool>
typedef pair<int,int> pll;
const int N=1e6+10;
const int inf=1e18;
const int mod=998244353;
void solve(){
int n;cin>>n;
vi p(n+10);
for(int i=1;i<=n;i++){
cin>>p[i];
}
deque<pll> dq;
vector<int> mp(n+1);
int mex=0;
int sum=0;
for(int i=1;i<=n;i++){
mp[p[i]]=true;
while(mp[mex]){
mex++;
}
dq.push_back({mex,1}); //second表示数量
sum += mex;
}
int ans=sum;
for(int i=1;i<n;i++){
pll me={p[i],0};
sum-=dq.front().first;
dq.front().second--;
if(dq.front().second==0){
dq.pop_front();
}
while(!dq.empty() && dq.back().first>=p[i]){
sum-=dq.back().first*dq.back().second;
me.second += dq.back().second;
dq.pop_back();
}
dq.push_back(me);
sum = sum + me.first*me.second;
dq.push_back({n,1});
sum+=n;
ans=max(ans,sum);
}
cout<<ans<<"\n";
}
signed main() {
vcoistnt
cout<<fixed<<setprecision(2);
int _=1;
cin>>_;
while(_--) solve();
return 0;
}Day8------2025.4.1
D. Recommendations(数据结构+二分set的应用)
思路
此题思路并不难想,第一遍尝试试图将所有区间按照 l 从小到大排序,试图遍历一遍统计左右端点的值,发现按照此排序我们只能保证前面的左端点能够包含后面的,并不能在复杂度允许的情况下将左边的值统计
因此便想到了两次遍历,第一次按照l从小到大排序,如果l相等则r小的在上,这样在遍历到i位置时我们确保了,i之前的 l 是能包含 i 位置的,我们只需要找到 i 之前位置中最大的r,统计答案
如样例3按照此排序后
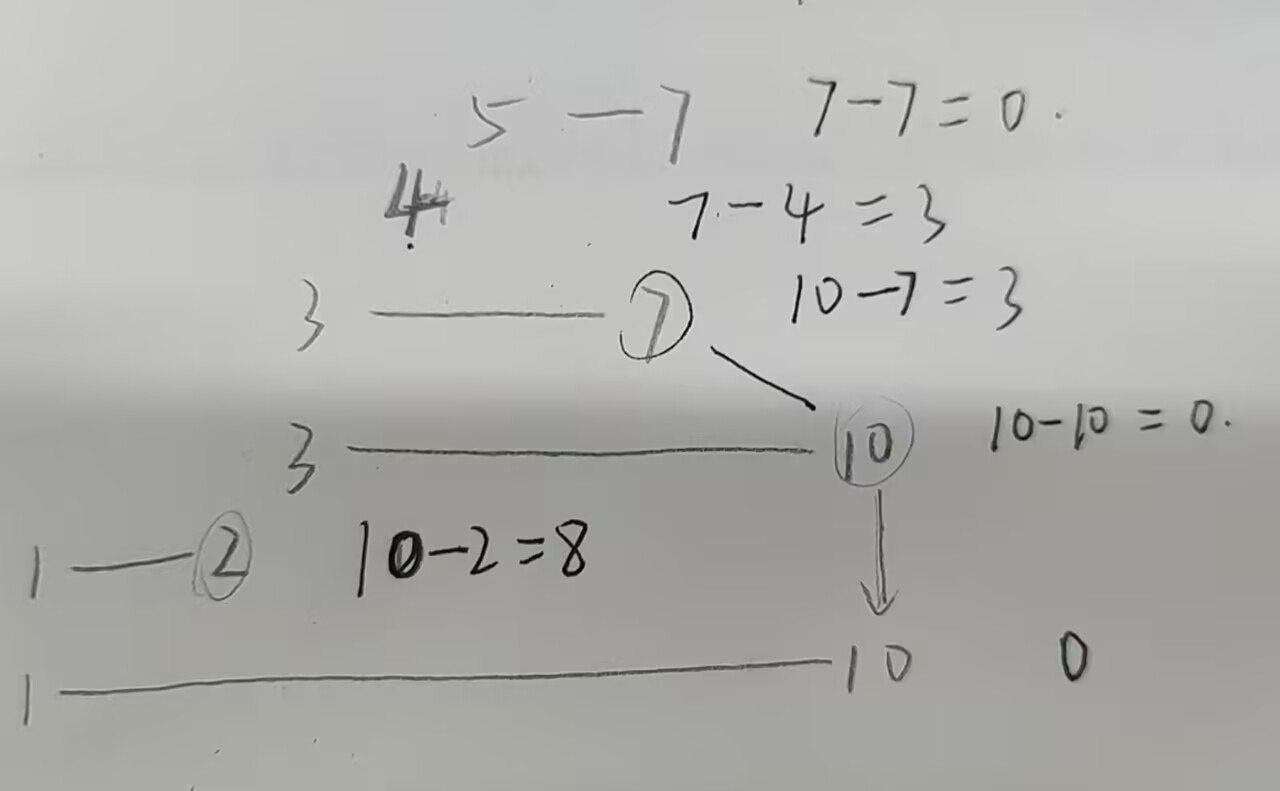
第二次遍历按照r从小到大排序,如果r相等则将l大的放后面,这样便能保证前面的r是包含当前的r的,统计答案即可
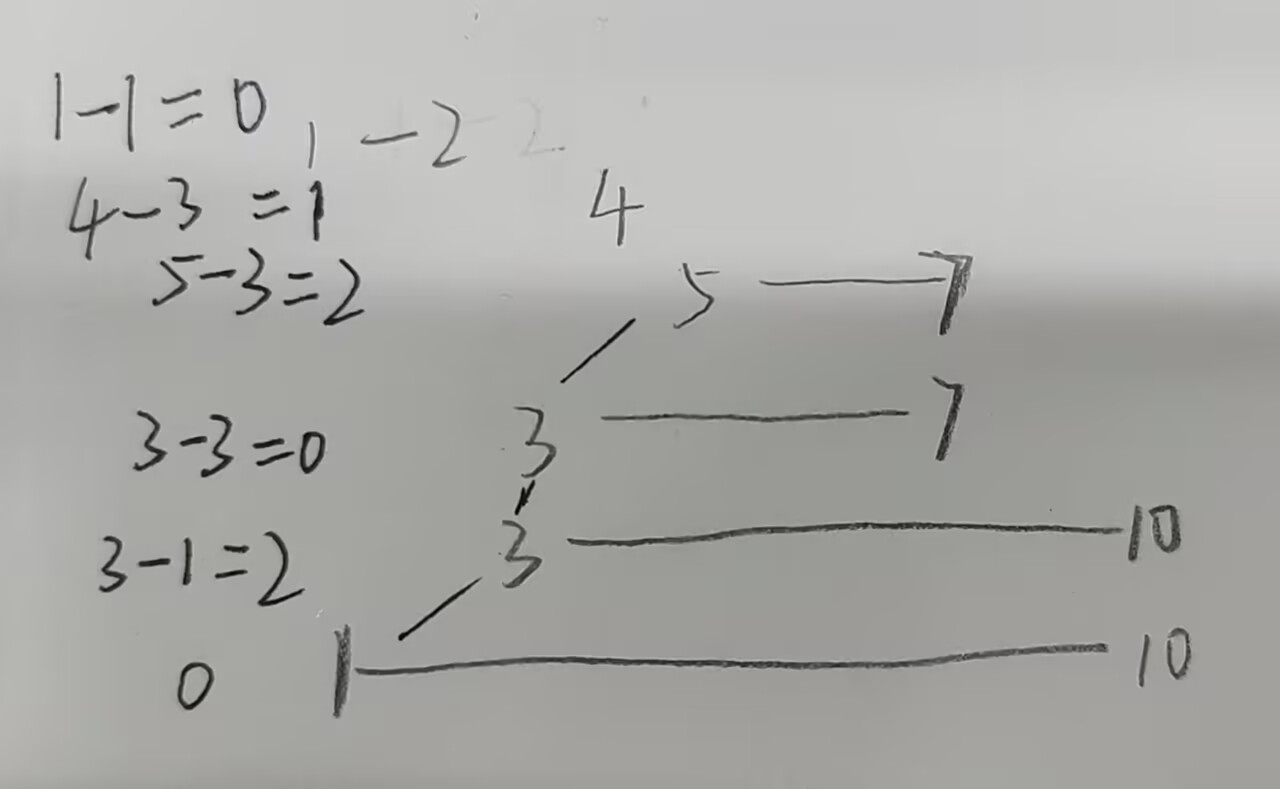
注意此处用set实现,如果用数组的化会T5,

代码
#include<bits/stdc++.h>
using namespace std;
#define vcoistnt ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
#define int long long
#define vi vector<int>
#define vb vector<bool>
typedef pair<int,int> pll;
const int N=2e5+10;
const int inf=1e18;
const int mod=998244353;
struct node{
int l,r,id;
};
bool cmpl(node x,node y){
if(x.l==y.l){
return x.r>y.r;
}
return x.l<y.l;
}
bool cmpr(node x,node y){
if(x.r==y.r){
return x.l<y.l;
}
return x.r>y.r;
}
void solve(){
int n;cin>>n;
vector<node> p(n+10);
for(int i=1;i<=n;i++){
cin>>p[i].l>>p[i].r;
p[i].id=i;
}
vi ansr(n+10); //记录右边
sort(p.begin()+1,p.begin()+1+n,cmpl); //按照l从大到小排序
//保证在i之前的区间的右端点在i区间外
set<int> lv; //记录已经处理区间的右端点便于查找当前位置的右数量
lv.insert(p[1].r);
ansr[p[1].id]=0;
for(int i=2;i<=n;i++){
if(p[i].l==p[i-1].l&&p[i].r==p[i-1].r){
ansr[p[i].id]=0;
ansr[p[i-1].id]=0;
}else{
//目的时找到此前大于p[i].r的右端点的最小值
auto u=lv.lower_bound(p[i].r);
if(u==lv.end()){ //没有比它大的
ansr[p[i].id]=0;
}else{
ansr[p[i].id]=(*u-p[i].r);
}
}
lv.insert(p[i].r);
}
vi ansl(n+10);
sort(p.begin()+1,p.begin()+1+n,cmpr); //按照r从大到小排序
set<int> rv;
rv.insert(p[1].l);
ansl[p[1].id]=0;
for(int i=2;i<=n;i++){
if(p[i].l==p[i-1].l&&p[i].r==p[i-1].r){
ansl[p[i].id]=0;
ansl[p[i-1].id]=0;
}else{
auto u=rv.upper_bound(p[i].l);
if(u==rv.begin()){
ansl[p[i].id]=0;
}else{
--u;
ansl[p[i].id]=(p[i].l-*u);
}
}
rv.insert(p[i].l);
}
for(int i=1;i<=n;i++){
cout<<ansl[i]+ansr[i]<<"\n";
}
}
signed main() {
vcoistnt
cout<<fixed<<setprecision(2);
int _=1;
cin>>_;
while(_--) solve();
return 0;
}A. Adrenaline Rush(构造+模拟过程)
思路
对于i<j来说如果ai<aj想要最大化数量那么必然是aj超越ai,ai再超越bi
如果ai>aj,肯定是ai超越aj一次
我们便模拟此过程,发现如果我们从1 2 3...到a是比较难写的,那么我们不妨反过来,从a到1 2 ...
之后再将答案反转即可
代码
#include<bits/stdc++.h>
using namespace std;
#define vcoistnt ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
#define int long long
#define vi vector<int>
#define vb vector<bool>
typedef pair<int,int> pll;
const int N=2e5+10;
const int inf=1e18;
const int mod=998244353;
void solve(){
int n;
cin>>n;
vi a(n+10);
for(int i=1;i<=n;i++){
cin>>a[i];
}
vector<pll> ans;
for(int i=1;i<=n;i++){
for(int j=1;j<n;j++){
if(a[j]<a[j+1]){
swap(a[j],a[j+1]);
ans.push_back({a[j+1],a[j]});
}
}
}
for(int i=1;i<=n;i++){
for(int j=1;j<n;j++){
if(a[j]>a[j+1]){
swap(a[j],a[j+1]);
ans.push_back({a[j+1],a[j]});
}
}
}
reverse(ans.begin(),ans.end());
cout<<ans.size()<<"\n";
for(int i=0;i<ans.size();i++){
cout<<ans[i].first<<" "<<ans[i].second<<"\n";
}
}
signed main() {
vcoistnt
cout<<fixed<<setprecision(2);
int _=1;
// cin>>_;
while(_--) solve();
return 0;
}Day7------2025.3.28
B. Floor or Ceil(贪心+经验)
思路
一看div2B题直接暴力遇到奇数执行操作2偶数执行操作1结果WA2
在二进制下观察x的变化。
考虑最小值,我们发现无论进行多少次的操作2最多只能使得执行完m次操作后上一位进位,然后执行n次操作可能会把进位给消掉,这样就是最小值,可以多试一下几个样例便于理解,如n=1,m=3,
考虑最大值,先进行n次操作1,再进行m次操作2,这样得到的就是最大值,考虑如果穿插着进行的话那么操作1就可能会把操作2的进位给消掉
代码
void solve(){
int x,tn,tm;
cin>>x>>tn>>tm;
int n,m;
n=tn;m=tm;
int mi=x;
while(m--){
mi=(mi+1)/2;
if(mi<=1) break;
}
while(n--){
mi/=2;
if(!mi) break;
}
int mx=x;
n=tn;m=tm;
while(n--){
mx/=2;
if(!mx) break;
}
while(m--){
mx=(mx+1)/2;
if(mx<=1) break;
}
cout<<mi<<" "<<mx<<"\n";
}
D. Tree Jumps(树上dp?)
思路
很简单的一道动态规划的题目,我们设dp[i]为以节点i为节点的路径数量,答案即所有节点之和
状态转移涉及到了树形结构,我们当前节点i的路径数其实就是以上一层节点为结尾的路径数之和(除与节点i相连的节点)
代码
#include<bits/stdc++.h>
using namespace std;
#define vcoistnt ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
#define int long long
#define vi vector<int>
#define vb vector<bool>
typedef pair<int,int> pll;
const int N=2e5+10;
const int inf=1e18;
const int mod=998244353;
void solve(){
int n;
cin>>n;
vector<vi> edge(n+10);
vi p(n+10);
for(int i=2;i<=n;i++){
cin>>p[i];
edge[p[i]].push_back(i);
}
vi dep(n+1); //节点i的深度
vector<vi> h(n+1); //深度为i的节点
int mx=1; //最大深度
vi dp(n+10); //以节点i结尾的路径数
dp[1]=1;
int sum=0; //表示上一层的路径数和
auto dfs=[&](auto self,int x,int fa)->void{
dep[x]=dep[fa]+1;
if(dep[x]==2){ //预处理第二层
dp[x]=1;
sum++;
}
mx=max(mx,dep[x]);
h[dep[x]].push_back(x);
for(auto y:edge[x]){
if(y==fa) continue;
self(self,y,x);
}
};
dfs(dfs,1,0);
for(int i=3;i<=mx;i++){ //遍历深度
int tsum=0;
for(auto x:h[i]){
dp[x]=(sum-dp[p[x]]+mod)%mod;
tsum=(tsum+dp[x])%mod;
}
sum=tsum;
}
int ans=0;
for(int i=1;i<=n;i++){
ans=(ans+dp[i])%mod;
}
cout<<ans<<"\n";
}
signed main() {
vcoistnt
cout<<fixed<<setprecision(2);
int _=1;
cin>>_;
while(_--) solve();
return 0;
}Day6------2025.3.20
今天就补一道2300的题,刚学的笛卡尔树
E. Yet Another Array Counting Problem(笛卡尔树+树形dp)
思路
笛卡尔树对可能性的划分是很好的,那么这题就深刻体现出来了,我们对a数组进行按大根堆的要求建立笛卡尔树,并且因为有相等的数那么我们要求相等的数在单调栈中可以压着相等的数
那么我们根据数组a构造的笛卡尔树来构造数组b,我们发现对于某个节点我们设其值为x,那么根据题意我们此节点的左孩子上的数必须<=x-1,右孩子上的数<=x
这样就能保证如果选择的区间包含此节点以及它的子树,那么最左端最大值就是这个数的位置
来个具体例子来直观的展示一下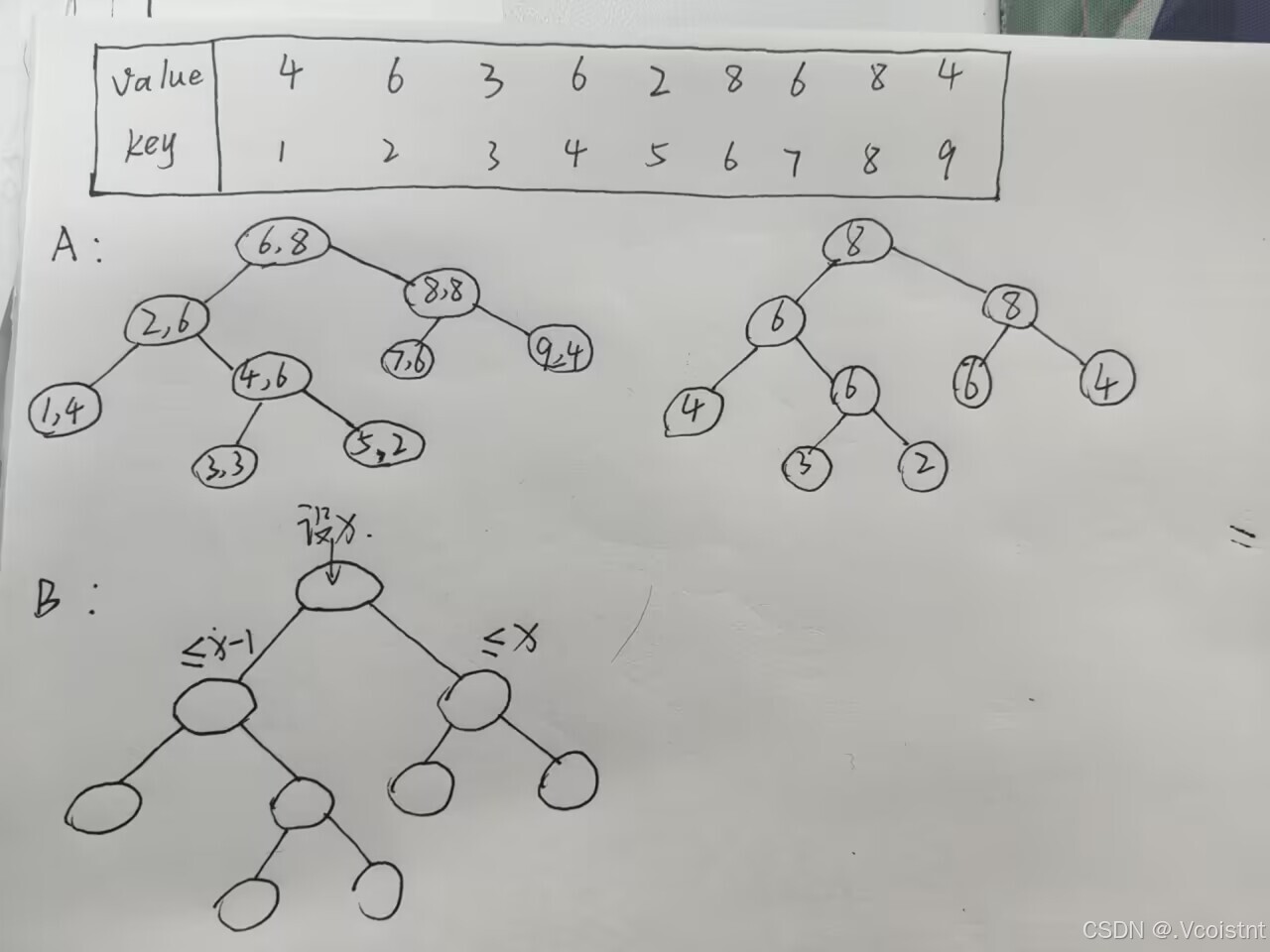
那么接下来就是统计B数上的数量总数了,这得用树形dp来实现
我们设表示当前来到的节点,其值是j时的数量
设表示u节点其值小于等于 j 的数量
那么状态转移方程为:
u表示当前节点,ls rs为左右孩子
最后答案便是 s表示头节点
代码
#include<bits/stdc++.h>
using namespace std;
#define vcoistnt ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
#define int long long
#define vi vector<int>
#define vb vector<bool>
typedef pair<int,int> pll;
const int N=2e5+10;
const int inf=1e18;
const int mod=1e9+7;
void solve(){
int n,m;
cin>>n>>m;
vi a(n+10);
for(int i=1;i<=n;i++){
cin>>a[i];
}
//构造笛卡尔树
vi ls(n+10),rs(n+10),sta(n+10);
auto build=[&]()->void{
int top=0;
for(int i=1;i<=n;i++){
int pos=top;
while(pos>0 && a[sta[pos]]<a[i]){
pos--;
}
if(pos>0){
rs[sta[pos]] = i;
}
if(pos<top){
ls[i]=sta[pos+1];
}
sta[++pos]=i;
top=pos;
}
};
build();
//树形dp
int s=sta[1];
vector<vi> dp(n+10,vi(m+10));
for(int j=0;j<=m;j++){
dp[0][j]=1;
}
auto dfs=[&](auto self,int u)->void{
if(ls[u]!=0){
self(self,ls[u]);
}
if(rs[u]!=0){
self(self,rs[u]);
}
vi tep(m+10);
for(int j=1;j<=m;j++){
tep[j]=(dp[ls[u]][j-1]*dp[rs[u]][j])%mod;
dp[u][j]=(dp[u][j-1]+tep[j])%mod;
}
};
dfs(dfs,s);
cout<<dp[s][m]<<"\n";
}
signed main() {
vcoistnt
cout<<fixed<<setprecision(2);
int _=1;
cin>>_;
while(_--) solve();
return 0;
}Day5------2025.3.19
C. Math Division(数学+dp)
思路
感觉这题确实需要很大的思维吧,想了半天没想出来看了题解才恍然大悟
首先可以明确的是我们需要 n或n-1 次操作就能把x变成1,我们再想一下什么时候进行n次操作,什么时候进行n-1次操作?
我们发现当n-1位发生进位时我们就需要n次操作,不发生进位时就是n-1次操作
不妨设为第i位发生进位的概率。
1.s[i]==0时只有在i-1发生进位使得s[i]=1才能有1/2的概率发生进位
2.s[i]==1时在 i-1 发生进位的时候 i 就会发生进位,i-1不发生进位我们有1/2的概率发生进位
答案便是
i-1发生进位时n次操作,不发生进位时n-1次操作
代码
#include<bits/stdc++.h>
using namespace std;
#define vcoistnt ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
#define int long long
#define vi vector<int>
#define vb vector<bool>
typedef pair<int,int> pll;
const int N=2e5+10;
const int inf=1e18;
const int mod=1e9+7;
int ksm(int a,int b){
int ans=1;
while(b){
if(b&1){
ans=(ans*a)%mod;
}
a=((a%mod)*(a%mod))%mod;
b>>=1;
}
return ans;
}
int inverse(int a){
return ksm(a,mod-2);
}
void solve(){
int n;
cin>>n;
string s;
cin>>s;
s=" "+s;
reverse(s.begin()+1,s.begin()+1+n);
vi dp(n+10); //表示第i位发生进位的概率
for(int i=1;i<=n;i++){
if(s[i]=='0'){
dp[i]=dp[i-1]*(inverse(2))%mod;
}else{
dp[i]=(dp[i-1]+1)*(inverse(2))%mod;
}
}
cout<<n-1+dp[n-1]<<"\n";
}
signed main() {
vcoistnt
cout<<fixed<<setprecision(2);
int _=1;
cin>>_;
while(_--) solve();
return 0;
}A. Scrambled Scrabble(暴力枚举+贪心)
思路
我们先忽略Y和NG的情景,发现答案,s是最长单词长度,v是元音数量,c是辅音数量
接下来我们将Y和NG的情况考虑进去,我们可以直接枚举NG的使用个数,以及Y当元音以及辅音的个数,统计所有情况,得出答案即可
代码
#include<bits/stdc++.h>
using namespace std;
#define vcoistnt ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
#define int long long
#define vi vector<int>
#define vb vector<bool>
typedef pair<int,int> pll;
const int N=2e5+10;
const int inf=1e18;
const int mod=1e9+7;
map<char,bool> mp;
void solve(){
string s;
cin>>s;
int n=s.size();
int cntv=0,cnty=0,cntn=0,cntg=0,cntc=0;
for(int i=0;i<n;i++){
if(mp[s[i]]){
cntv++;
}else if(s[i]=='Y'){
cnty++;
}else if(s[i]=='N'){
cntn++;
}else if(s[i]=='G'){
cntg++;
}else{
cntc++;
}
}
int t=min(cntn,cntg); //NG组合的数量
int ans=0;
for(int i=0;i<=t;i++){ //使用NG组合的数量
for(int j=0;j<=cnty;j++){ //把Y当元音使用的数量
int v=j+cntv; //元音数
int c=cntc+(cnty-j)+(cntn-i)+(cntg-i)+i; //辅音数量
ans=max(ans,3*min(v,(c/2))+min(2*v,i));
}
}
cout<<ans<<"\n";
}
signed main() {
vcoistnt
cout<<fixed<<setprecision(2);
mp['A']=true;
mp['E']=true;
mp['I']=true;
mp['O']=true;
mp['U']=true;
int _=1;
// cin>>_;
while(_--) solve();
return 0;
}Day1------2025.3.13
D. Palindrome Shuffle(二分贪心字符串处理)
思路
首先将两头相等的字符串先去掉,此部分已经满足回文不考虑,去掉之后我们发现我们所要寻找的长度一定是包含头或者包含尾的一段区间,我们可以将字符串正向和反向各自用二分找一下最短成立的长度去最小值即可
至于具体的check函数,我们假设当前所确定的长度为x,那么先将1---x的字符统计,首先分两种情况
x>=n/2,我们只需要看剩下的字符是否在前x个中出现过即可,这样就能通过改变顺序构成回文
x<n/2时,我们不仅要看后x字符是否与在前x个字符数量相同,还要看中间的字符是否是回文才行
代码
#include<bits/stdc++.h>
using namespace std;
#define vcoistnt ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
#define int long long
#define vi vector<int>
#define vb vector<bool>
typedef pair<int,int> pll;
const int N=2e5+10;
const int inf=1e18;
const int mod=998244353;
void solve(){
string s;
cin>>s;
int n=s.size();
s=" "+s;
int k=1;
while((k<=n/2)&&s[k]==s[n-k+1]){
k++;
}
n-=2*(k-1);
s=s.substr(k,n);
s=" "+s;
auto check=[&](int x)->bool{
vector<int> cnt(26);
for(int i=1;i<=x;i++){
cnt[s[i]-'a']++;
}
for(int i=1;i<=min(n-x,n/2);i++){
char c=s[n-i+1];
if(i<=x){
if(cnt[c-'a']<=0){
return false;
}
cnt[c-'a']--;
}else{
if(s[i]!=c){
return false;
}
}
}
return true;
};
int ans=n;
for(int z=0;z<2;z++){
int l=0,r=n;
while(l<=r){
int mid=l+r>>1;
if(check(mid)){
ans=min(ans,mid);
r=mid-1;
}else{
l=mid+1;
}
}
reverse(s.begin()+1,s.begin()+1+n);
}
cout<<ans<<"\n";
}
signed main() {
vcoistnt
cout<<fixed<<setprecision(2);
int _=1;
cin>>_;
while(_--) solve();
return 0;
}G. Skibidus and Capping(数论组合数欧拉筛)
思路
其实就是一个数学的问题,但要用到一些预处理以及欧拉筛的优化
具体而言所有的数量分为三种情况,
1.在所有素数里面选两个(如 2 3)然后删去选的是两个相同素数的情况(如 2 2),两个素数的lcm就一定是半素数
2.选择半素数和半素数的因子(如4 2,9 3)
3.可以单独选择一个半素数以及两个相同的半素数(如 4 4)
我们可以用欧拉筛来判断素数以及预处理一下半素数
代码
#include<bits/stdc++.h>
using namespace std;
#define vcoistnt ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
#define int long long
#define vi vector<int>
#define vb vector<bool>
typedef pair<int,int> pll;
const int N=2e5+10;
const int inf=1e18;
const int mod=998244353;
vector<int> minp,primes;
vb vis(N,false);
void sieve(int n){
minp.assign(n+1,0);
primes.clear();
for(int i=2;i<=n;i++){
if(minp[i]==0){
minp[i]=i;
primes.push_back(i);
}
for(auto p:primes){
if(i*p>n){
break;
}
minp[i*p]=p;
if(p==minp[i]){
break;
}
}
}
}
bool isprime(int n){
return minp[n]==n;
}
void solve(){
int n;cin>>n;
vi a(n+10);
int cnt=0;
unordered_map<int,int> mp;
vi ans;
vi pr;
for(int i=1;i<=n;i++){
cin>>a[i];
if(isprime(a[i])){
pr.push_back(a[i]);
mp[a[i]]++;
cnt++;
}else{
ans.push_back(a[i]);
}
}
//素数里面选两个 如3 5
int res=0;
res+=(cnt*(cnt-1)/2);
for(auto [x,ct]:mp){
res-=(ct*(ct-1)/2);
}
//统计一个素数和半素数的数量。如2 4
for(int x:ans){
int ct=0;
if(vis[x]){
for(int j=2;j<=sqrt(x);j++){
if(x%j==0){
if(j!=x/j){
ct+=mp[j];
ct+=mp[x/j];
}else{
ct+=mp[j];
}
}
}
}
res+=ct;
}
//统计半素数之间的选择如 4 4 4
unordered_map<int,int> mpx;
for(int x:ans){
if(vis[x]){
mpx[x]++;
}
}
for(auto [x,y]:mpx){
res+=y+(y*(y-1)/2);
}
cout<<res<<"\n";
}
signed main() {
vcoistnt
cout<<fixed<<setprecision(2);
sieve(N);
int tn=primes.size();
for(int i=0;i<tn;i++){
for(int j=i;j<tn;j++){
if(primes[i]*primes[j]>200000){break;}
vis[primes[i]*primes[j]]=true;
}
}
int _=1;
cin>>_;
while(_--) solve();
return 0;
}Day2------2025.3.14
F. Skibidus and Slay(贪心树形结构)
思路
感觉此题相对而言比较简单主要是实现
此题我们只需要看相连的三个点即可,如果有两个数相同那么这个数就能够成为多数
代码
#include<bits/stdc++.h>
using namespace std;
#define vcoistnt ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
#define int long long
#define vi vector<int>
#define vb vector<bool>
typedef pair<int,int> pll;
const int N=2e5+10;
const int inf=1e18;
const int mod=998244353;
void solve(){
int n;
cin>>n;
vi a(n+10);
vi ans(n+10,0);
for(int i=1;i<=n;i++){
cin>>a[i];
}
vector<vi> g(n+10);
for(int i=1;i<n;i++){
int u,v;
cin>>u>>v;
g[u].push_back(v);
g[v].push_back(u);
}
for(int i=1;i<=n;i++){
map<int,int> mp;
mp[a[i]]++;
for(auto x:g[i]){
mp[a[x]]++;
}
for(auto [u,v]:mp){
if(v>=2) ans[u]=1;
}
}
for(int i=1;i<=n;i++){
cout<<ans[i];
}
cout<<"\n";
}
signed main() {
vcoistnt
cout<<fixed<<setprecision(2);
int _=1;
cin>>_;
while(_--) solve();
return 0;
}E. Resourceful Caterpillar Sequence(博弈贪心)
思路
此题阿伦最后能赢得情况只有两种,
1.p位于非叶子节点而q位于叶子节点那么阿伦在没有进行游戏前便会胜利
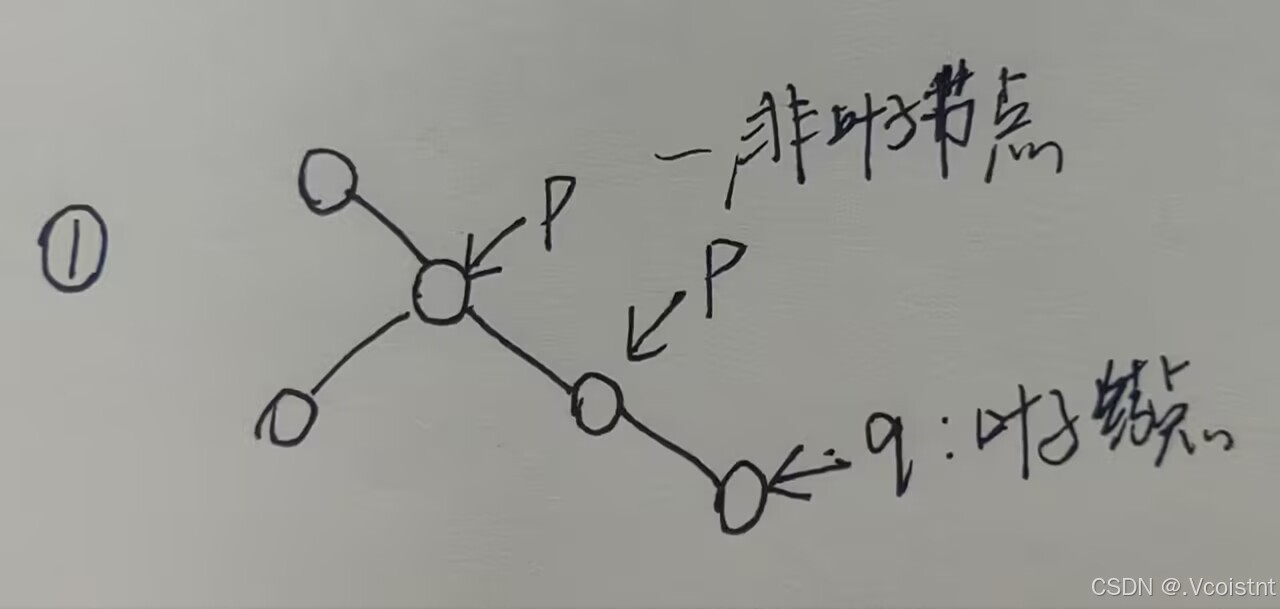
2.在p移动后并且没有移动到叶子节点,q也跟着往前移动之后发现有叶子节点与之相连,那么接下来阿伦只需要将q移动到叶子节点便会赢
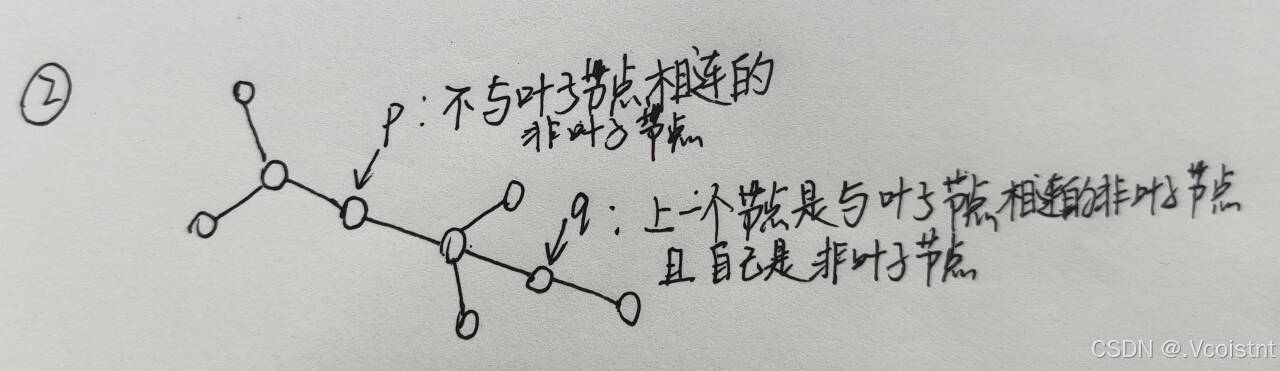
代码
#include<bits/stdc++.h>
using namespace std;
#define vcoistnt ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
#define int long long
#define vi vector<int>
#define vb vector<bool>
typedef pair<int,int> pll;
const int N=2e5+10;
const int inf=1e18;
const int mod=998244353;
void solve(){
int n;
cin>>n;
vector<vi> g(n+10);
for(int i=1;i<n;i++){
int u,v;
cin>>u>>v;
g[u].push_back(v);
g[v].push_back(u);
}
auto d=[&](int x)->int{
return g[x].size();
};
int ct1=0; //记录叶子节点的个数
int ct2=0; //记录非叶子节点的个数
int ct4=0; //记录那些非叶子节点且不连叶子节点的个数
int ans=0;
vector<int> dx(n+10); //记录节点i与 与叶子节点相连的非叶子节点 连接的非叶子节点的个数
for(int i=1;i<=n;i++){
if(d(i)<=1){
ct1++;
}else{
ct2++;
int cnt1=0,cnt2=0;
for(auto x:g[i]){
if(d(x)>=2) cnt1++; //非叶子节点
else cnt2++; //叶子节点
}
if(cnt2==0){
ct4++;
}else{
dx[i]=cnt1;
}
}
}
ans+=ct1*ct2;
for(int i=1;i<=n;i++){
if(dx[i]){
ans+=(ct4*(dx[i]-1));
}
}
cout<<ans<<"\n";
}
signed main() {
vcoistnt
cout<<fixed<<setprecision(2);
int _=1;
cin>>_;
while(_--) solve();
return 0;
}D. Refined Product Optimality(排序贪心二分数论)
思路
贪心地想可以发现对a和b排序之后取最小的累乘,这样得到的答案是最大的,现在问题就转变为了如何对某个数+1之后,重新排序以及怎样更新答案
对于排序来说我们每次只+1那么我们可以用二分来实现对数组的修改并维护排序
对于怎样更新答案,我们发现对于a数组与b数组的两个数x,y来说如果x<y但x+1之后,那么答案是就会变成,但如果是y+1答案就不会受到影响,此处还用到分数取余
还有就是一个需要注意的点是x是原数组的值需要额外开一个数组来存未排序之前的数
代码
#include<bits/stdc++.h>
using namespace std;
#define vcoistnt ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
#define int long long
#define vi vector<int>
#define vb vector<bool>
typedef pair<int,int> pll;
const int N=2e5+10;
const int inf=1e18;
const int mod=998244353;
int ksm(int a,int b){
int ans=1;
while(b){
if(b&1){
ans=(ans*a)%mod;
}
a=((a%mod)*(a%mod))%mod;
b>>=1;
}
return ans;
}
int inverse(int a){
return ksm(a,mod-2);
}
void solve(){
int n,q;
cin>>n>>q;
vi a(n+10);
vi b(n+10);
vi ta(n+10);
vi tb(n+10);
for(int i=1;i<=n;i++){
cin>>a[i];
ta[i]=a[i];
}
int ans=1;
for(int i=1;i<=n;i++){
cin>>b[i];
tb[i]=b[i];
}
sort(a.begin()+1,a.begin()+1+n);
sort(b.begin()+1,b.begin()+1+n);
for(int i=1;i<=n;i++){
ans*=(min(a[i],b[i]));
ans%=mod;
}
cout<<ans<<" ";
while(q--){
int o,x;
cin>>o>>x;
if(o==1){
int t=ta[x]+1;
ta[x]++;
int p=upper_bound(a.begin()+1,a.begin()+1+n,t-1)-a.begin();
a[p-1]=t;
if(b[p-1]>=a[p-1]){
ans=(ans*inverse(t-1)%mod*t)%mod;
}
}else{
int t=tb[x]+1;
tb[x]++;
int p=upper_bound(b.begin()+1,b.begin()+1+n,t-1)-b.begin();
b[p-1]=t;
if(a[p-1]>=b[p-1]){
ans=(ans*inverse(t-1)%mod*(t))%mod;
}
}
cout<<ans<<" ";
}
cout<<"\n";
}
signed main() {
vcoistnt
cout<<fixed<<setprecision(2);
int _=1;
cin>>_;
while(_--) solve();
return 0;
}Day3------2025.3.17
F. Fix Flooded Floor(动态规划)
思路
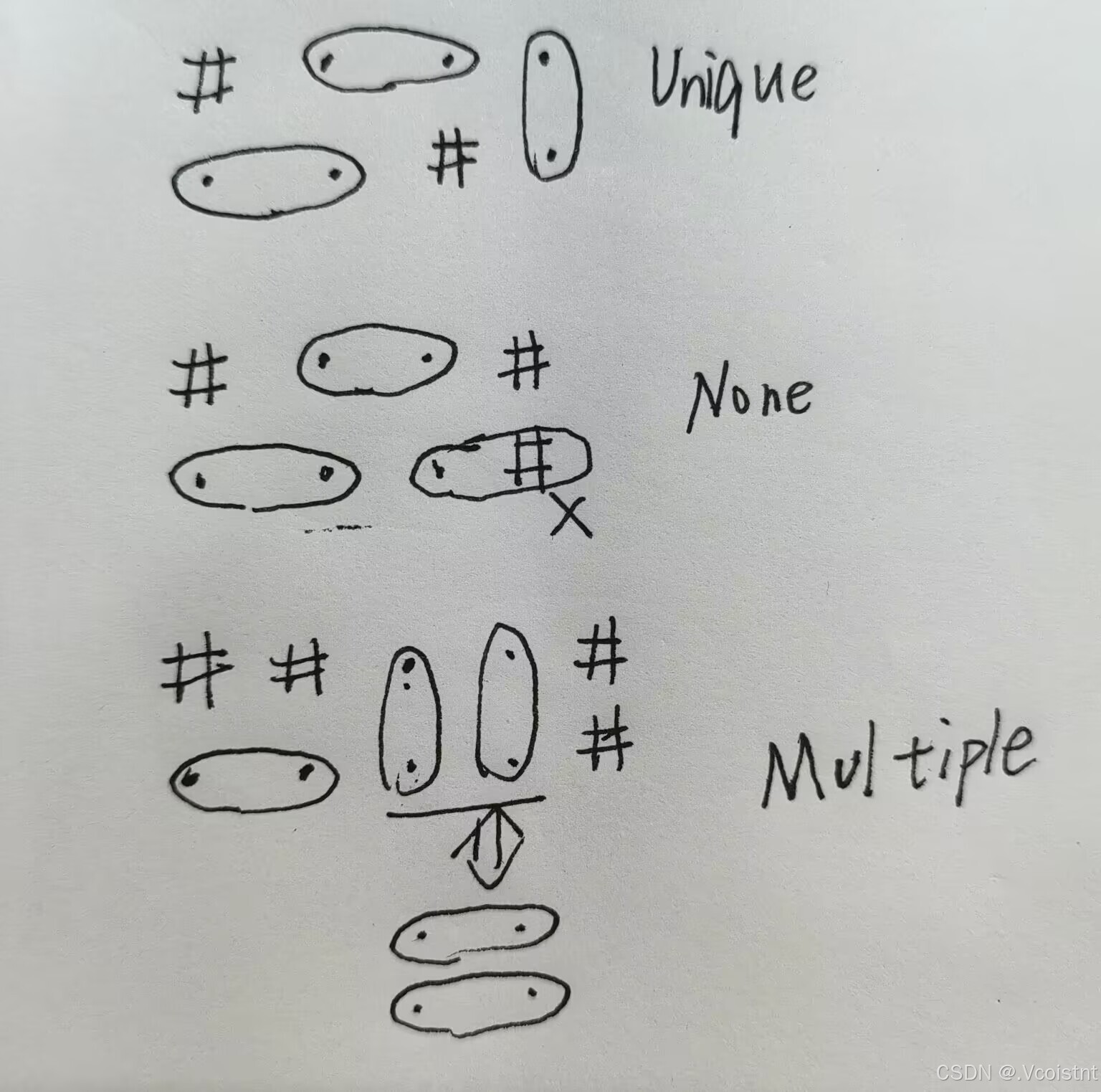
这题是贪心+动态规划,我们发现数据是2e5的,也就说明了我们需要在一次for循环遍历的情况下解决这个问题,当我们遍历到 i 位置时,我们只会出现四种情况,1“. .” 2“. #” 3“# .” 4“# #”
我们发现当前面没有残留的 “.” 需要去构造且出现1 4情况时是不会对后面产生影响的,其他情况也是如此如果有残留的“.”需要当前i位置的“.”去消除残留,看能否消除以及消除之后是否对后面有残留
方便理解来个例子
而其发现当出现四个.的时候我们会有多种可能
代码
#include<bits/stdc++.h>
using namespace std;
#define vcoistnt ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
#define int long long
#define vi vector<int>
#define vb vector<bool>
typedef pair<int,int> pll;
const int N=2e5+10;
const int inf=1e18;
const int mod=998244353;
void solve(){
int n;
cin>>n;
string x,y;
cin>>x>>y;
int now=0; //0前面没有残留,1第一行有.残留,2第二行有.残留
bool f=false; //看能否补好
bool b=false; //看是否有多种
for(int i=0;i<n;i++){
if(now==0){
if(i>0&&x[i]=='.'&&y[i]=='.'&&x[i-1]=='.'&&y[i-1]=='.') b=true;
if((x[i]=='.'&&y[i]=='.')||(x[i]=='#'&&y[i]=='#')){
now=0;
}else if(x[i]=='.'){
now=1;
}else{
now=2;
}
}else if(now==1){
if(x[i]=='#'){
f=true;break;
}else{
if(y[i]=='.'){
now=2;
}else{
now=0;
}
}
}else if(now==2){
if(y[i]=='#'){
f=true;break;
}else{
if(x[i]=='.'){
now=1;
}else{
now=0;
}
}
}
}
if(f||(now!=0)){
cout<<"None\n";
}else{
if(b){
cout<<"Multiple\n";
}else{
cout<<"Unique\n";
}
}
}
signed main() {
vcoistnt
cout<<fixed<<setprecision(2);
int _=1;
cin>>_;
while(_--) solve();
return 0;
}E. Expression Correction(模拟字符串处理)
思路
思路倒是不难难在实现上(真是史题),发现字符串的长度小于100,直接暴力枚举一遍每一种情况判断合不合法即可
代码
#include<bits/stdc++.h>
using namespace std;
#define vcoistnt ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
#define int long long
#define vi vector<int>
#define vb vector<bool>
typedef pair<int,int> pll;
const int N=2e5+10;
const int inf=1e18;
const int mod=998244353;
int mx=1e10;
void solve(){
string s;
cin>>s;
auto check=[&](string s)->bool{ //检查等式是否合法
if(!isdigit(s[0])||(!isdigit(s.back()))){
return false;
}
if(s[0]=='0'&&isdigit(s[1])) return false; //前导零同时要排除0=0这种情况
for(int i=1;i<s.size()-1;i++){
if(!isdigit(s[i-1])&&s[i]=='0'&&isdigit(s[i+1])) return false; //前导零
if(!isdigit(s[i])&&!isdigit(s[i-1])) return false; //两个符号相连的情况
}
int sig=1; //1表示+,2表示-
int ansl=0,ansr=0; //等式左右两边的值
int x=0; //当前值遇到符号清零
bool f=false; //判断等号左右
for(int i=0;i<s.size();i++){
if(isdigit(s[i])){
x*=10;
x+=(s[i]-'0');
if(x>=mx) return false;
}else{
if(s[i]=='-'){
if(sig==1){
if(!f) ansl+=x;
else ansr+=x;
}else{
if(!f) ansl-=x;
else ansr-=x;
}
x=0;
sig=2;
}else if(s[i]=='+'){
if(sig==1){
if(!f) ansl+=x;
else ansr+=x;
}else{
if(!f) ansl-=x;
else ansr-=x;
}
x=0;
sig=1;
}else{
if(sig==1){
if(!f) ansl+=x;
else ansr+=x;
}else{
if(!f) ansl-=x;
else ansr-=x;
}
f=true;
x=0;
sig=1;
}
}
}
if(sig==1){
ansr+=x;
}else{
ansr-=x;
}
// cout<<ansl<<" "<<ansr<<" ";
return ansl==ansr;
};
if(check(s)){
cout<<"Correct\n";return;
}
for(int i=0;i<s.size();i++){
string tl=s;
string tr=s;
if(isdigit(s[i])){
for(int j=i;j>=1;j--){
swap(tl[j],tl[j-1]);
if(check(tl)){
cout<<tl<<"\n";return;
}
}
for(int j=i;j<s.size()-1;j++){
swap(tr[j],tr[j+1]);
if(check(tr)){
cout<<tr<<"\n";return;
}
}
}
}
cout<<"Impossible\n";
}
signed main() {
vcoistnt
cout<<fixed<<setprecision(2);
int _=1;
// cin>>_;
while(_--) solve();
return 0;
}Day4------2025.3.18
G. Tree Destruction(树上dp)
思路
不难发现我们去掉一条路径,那么它形成的连通分量就是其中s是路径上的每个点的链接边的个数,k是这条路径上边的个数,对于一个点来说处于最佳路径上要么以此为顶点,要么以此为路径的上的一点
我们设表示以i为顶点的路径最多能形成多少个连通分量,
j表示i的子节点,du表示与i相连边的数量
设表示以 i 为路径上的一点最多能形成几个连通分量,如果只有一个子节点
,否则就取两个
最大的子节点相连
代码
#include<bits/stdc++.h>
using namespace std;
#define vcoistnt ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
#define int long long
#define vi vector<int>
#define vb vector<bool>
typedef pair<int,int> pll;
#define x first
#define y second
void solve(){
int n;cin>>n;
vector<vector<int>> g(n+10);
for(int i=1;i<n;i++){
int u,v;
cin>>u>>v;
g[u].emplace_back(v);
g[v].emplace_back(u);
}
vector<pll> dp(n+10);
auto dfs=[&](auto self,int x,int fa)->void{
dp[x].x=g[x].size();
int m1=-1,m2=-1;
for(auto y:g[x]){
if(y==fa) continue;
self(self,y,x);
dp[x].x=max(dp[x].x,dp[y].x+(int)g[x].size()-2);
m2=max(m2,dp[y].x);
if(m1<m2) swap(m1,m2);
}
dp[x].y=dp[x].x;
if(m2!=-1){
dp[x].y=m1+m2+g[x].size()-4;
}
};
dfs(dfs,1,0);
int ans=0;
for(int i=1;i<=n;i++){
ans=max(ans,max(dp[i].x,dp[i].y));
}
cout<<ans<<"\n";
}
signed main() {
vcoistnt
cout<<fixed<<setprecision(2);
int _=1;
cin>>_;
while(_--) solve();
return 0;
}A. Iris and Game on the Tree
思路
我们首先得观察出一个结论那就是10串和01串的数量是否相等与首尾的字符是否相等有关,如果首尾字符相等那么01 10是相等的,否则就不相等
那么问题便转化为了只看根节点和叶子节点的字符
1.如果根节点是确定的,我们只需要看叶子节点0多还是1多
2.如果根节点不确定,作为先手我们首先要把根节点填成与叶子节点已经确定出现次数最多的不同的那个。如果出现次数是相等的我们先手填叶子节点是亏的,那么就需要非叶子节点并且不确定的节点数来转换先手,这样我们要讨论非叶子节点中?的奇偶
代码
#include<bits/stdc++.h>
using namespace std;
#define vcoistnt ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
#define int long long
#define vi vector<int>
#define vb vector<bool>
typedef pair<int,int> pll;
const int N=2e5+10;
const int inf=1e18;
const int mod=998244353;
void solve(){
int n;
cin>>n;
vector<vi> g(n+10);
for(int i=1;i<n;i++){
int u,v;
cin>>u>>v;
g[u].push_back(v);
g[v].push_back(u);
}
string s;cin>>s;s=" "+s;
int f=false; //判断根节点是否确定
if(s[1]!='?') f=true;
int ct1=0,ct0=0; //记录叶子节点0 1的数量
int ct=0; //记录叶子节点为?的数量
//写完后发现只需要一遍for循环即可不需要遍历树
// auto dfs=[&](auto self,int x,int fa)->void{
// if(s[x]=='?') cnt++;
// if(x!=1&&g[x].size()==1){
// if(s[x]=='0') ct0++;
// if(s[x]=='1') ct1++;
// if(s[x]=='?') ct++;
// }
// for(auto y:g[x]){
// if(y==fa) continue;
// self(self,y,x);
// }
// };
// dfs(dfs,1,0);
int cnt=0; //记录?的个数
for(int i=1;i<=n;i++){
if(s[i]=='?') cnt++;
if(i!=1&&g[i].size()==1){
if(s[i]=='0') ct0++;
if(s[i]=='1') ct1++;
if(s[i]=='?') ct++;
}
}
cnt=cnt-ct; //将cnt更改为非叶子节点?的数量
if(f){
if(s[1]=='1'){
cout<<ct0+(ct+1)/2<<"\n";
}else{
cout<<ct1+(ct+1)/2<<"\n";
}
}else{
if(ct1!=ct0)
cout<<max(ct1,ct0)+ct/2<<"\n";
else{
if(cnt%2){
cout<<ct1+ct/2<<"\n";
}else{
cout<<ct1+(ct+1)/2<<"\n";
}
}
}
}
signed main() {
vcoistnt
cout<<fixed<<setprecision(2);
int _=1;
cin>>_;
while(_--) solve();
return 0;
}























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








