动态规划（简单习题）

数字三角形 Number Triangles

首先我看到这个题目就在思考应该用怎样一个数据结构来存放这些数据，是二叉树，还是并查集那样的连接。
第二个问题这个使用动态规划应该怎样构建状态转移方程，使用dfs来遍历然后使用一个数组来存放最大价值吗？ 

针对第一个问题我们竟然要使用一个二维数组来存放（是我想复杂了，直接用二维数组来存就好了，应为下一层判断大打谁小然后再直接放进去就可以了）

思路一：从下而上

从倒数第二层开始，将每个下一层相邻的两个数分别与这个数进行相加，然后使用max函数判断那个大，那个大这个数就存下这个数 其状态转移方程就是dp[i][j]+=max(dp[i+1][j],dp[i+1][j+1]);（需要注意的是我的这个是自加，第一次写就是没有自加导致的错误）

这个思路值得学习的地方就是：第一使用了二维数组进行存放了数据，第二就是从下而上。

代码如下：

#include<iostream>
#include<algorithm>
using namespace std;
const int N=1000+10;
int dp[N][N];
int main()
{
	int n;
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=i;j++)
		{
			cin>>dp[i][j];
		}
	}
	for(int i=n-1;i>=1;i--)
	{
		for(int j=1;j<=i;j++)
		{
			dp[i][j]+=max(dp[i+1][j],dp[i+1][j+1]);//这里是自加
		}
	}
	cout<<dp[1][1]<<endl;//那么最后开头的数就是最大的数
	
	return 0;
}

思路二：使用dfs（虽然这个时间会爆，但是可以复习一下dfs）自上而下

我看题解定义的dfs函数都是使用int类型来定义的，但是由于我写dfs函数的时候常常用void类型，所以我就是使用void类型来写一个dfs函数的思路吧。

首先就是考虑使用那种数据结构来存放数据，这里还是使用一个二维数组来存放数据，这个dfs函数终止条件就是当检查到最后一层的就可以停止了，但是实际上是要比最后一层，多一层但是说句实话我现在一般这种退出条件都是试出来的，我具体也不知道是怎么得出来的。

其实这里是不需要一个检查是否已经走过的检查数组，因为方向都是向下的，不会出现返祖现象，所以可以不需要vis数组，节省空间

代码如下：

#include<iostream>
#include<algorithm>
using namespace std;
const int N=1000+10;
int dp[N][N];
//int vis[N][N];
int maxN=-1;
int n;
void dfs(int x,int y,int sum)
{
	if(x>=n+1)
	{
		maxN=max(maxN,sum);
		return ;
	}
//	if(vis[x][y]==1)
//	return ;
//	vis[x][y]=1;
	dfs(x+1,y,sum+dp[x][y]);
	dfs(x+1,y+1,sum+dp[x][y]);
//	vis[x][y]=0;
	return ;
}
int main()
{
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=i;j++)
		{
			cin>>dp[i][j];
		}
	}
	dfs(1,1,0);
	cout<<maxN<<endl;
	return 0;
}

疯狂的采药

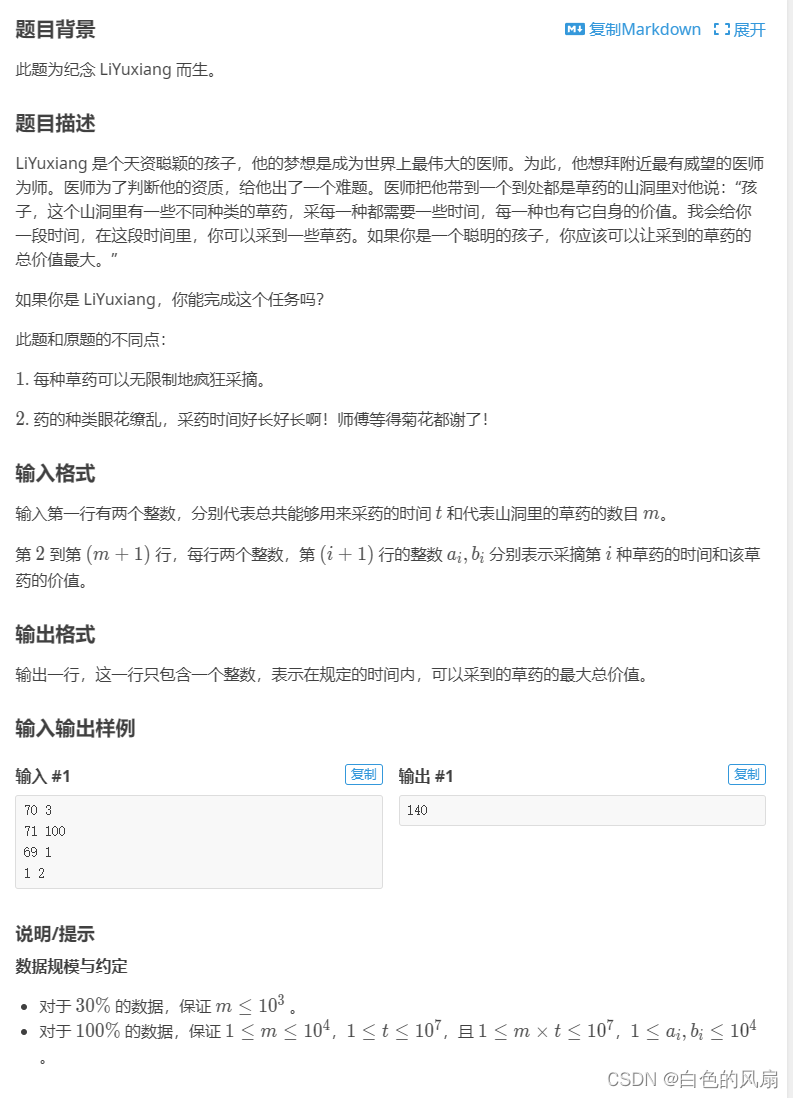 这是一个非常典型的完全背包问题，好了那么问题就来了，01背包和完全背包的区别是什么？
01背包对所有物品只能取一次，而完全背包所有物品可以取无限次。那么怎么体现这个区别呢？
01背包每次取最优解都是在上行中，所以在状态转移方程中取最优时是dp[j],而在01背包中是dp[j-1]，这个就是完全背包和01背包的区别。
  关于背包问题还有值得注意的是最后的取值是下标为背包容量最大的时候。

代码如下

#include<iostream>
#include<algorithm>
using namespace std;
const int N=100000;
const int M=1e7+10;
unsigned long long dp[M];
unsigned long long w[N];
unsigned long long v[N];
unsigned long long sum=0,n;
int main()
{
	cin>>sum>>n;
	for(int i=1;i<=n;i++)
	{
		cin>>w[i]>>v[i];
	}
	for(int i=1;i<=n;i++)
	{
		for(int j=w[i];j<=sum;j++)
		{
			dp[j]=max(dp[j],dp[j-w[i]]+v[i]);//如果是01背包问题那么就是max(dp[j-1],dp[j-w[i]]+v[i])
		}
	}
	cout<<dp[sum];//无论是01背包还是完全背包 最后的答案都是取容量最大的时候
	return 0;
}