水塘抽样算法

在大数据处理中，我们经常需要从海量数据中抽取一部分样本进行分析。然而，当数据量非常大时，传统的抽样方法可能面临时间和空间的挑战。水塘抽样算法为我们提供了一种高效且等概率的抽样方法，适用于处理大规模数据集或数据流。

算法逻辑

我们假定样本量n,需要的样本数量为m

遍历样本，前m个元素直接选取为样本。

从第K(K>m)个元素开始，随意生成一个范围在1~K的随机数，若该随机数大于m，保留该元素，随机丢弃原有m个元素中的一个，即对于第K(K>m)个元素，以概率m/K来决定是否保留该元素。

通过上述步骤，水塘抽样算法能够在遍历数据流的过程中，以等概率的方式选取样本。这种方法的优势在于，它只需要固定数量的内存空间（即m个元素的空间），就可以完成大规模数据流的等概率抽样。

等概率证明

为了帮助大家理解，我们以上图为例，为大家证明水塘抽样算法以等概率的方式选取样本。

对于前10个元素

他们被选取的概率为1。下面我们来计算它们留存的概率：

当遍历当第11个元素时，他被保留的概率为 m/K , 即 10/11 ,  此时需要替换原有元素，以A为例，A被选中的概率为 1/10 ，此时A被舍弃的概率为 (10/11)X(1/10)= 1/11，即A被保留的概率为 10/11。

我们向后遍历。可以算出当K= 12 , 13 , 14 , 15 ,16 时，选中A舍弃的概率为 11/12，12/13，13/14，14/15 ， 15/16。所以当遍历完数据后，A留存的概率为他们相乘即 10/16。因为舍弃时为随机等概率舍弃，所以前10个元素留存的概率均为 10/16！

对于后6个元素

以第11个元素B为例，他被选取的概率为 10/11（m/K） 。在后面的遍历中,他被留存的概率为 11/12，12/13，13/14，14/15 ， 15/16。当遍历完数据后，B留存的概率为他们相乘即 10/16。其他五个元素算法相同概率均为 10/16。

拓展到一般情况

对于前m个元素他们留存的概率为：

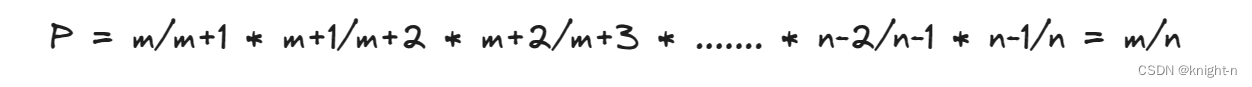
对于前n-m个元素他们留存的概率为：

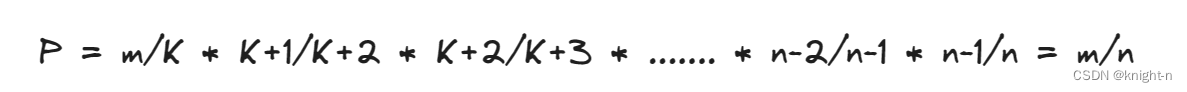
由此得证水塘抽样算法以等概率的方式选取样本。

代码实现

std::vector<int> reservoir_sampling(const std::vector<int>& population, int sample_size) 
{
    if (sample_size > population.size()) {
        throw std::invalid_argument("Sample size exceeds population size");
    }

    std::vector<int> reservoir(sample_size);
    std::default_random_engine rng(std::chrono::system_clock::now().time_since_epoch().count());

    // 初始化
    std::copy_n(population.begin(), sample_size, reservoir.begin());

    // 计算剩余待抽样元素数量
    int remaining = population.size() - sample_size;

    for (int i = sample_size; i < population.size(); ++i) {
        // 生成 [0, i] 区间内的随机整数
        std::uniform_int_distribution<> distr(0, i);

        // 以 1/i 的概率替换当前 reservoir 中的一个元素
        int j = distr(rng);
        if (j < sample_size) {
            reservoir[j] = population[i];
        }
    }

    return reservoir;
}