海星优化算法的研究总结

海星优化算法（starfish optimization algorithm，SFOA）是一种新型的启发式算法，该算法模拟了海星的探索、捕食和再生行为。SFOA包括勘探和开发两个主要阶段。探索阶段采用五维和一维相结合的混合搜索模式，模拟海星的探索行为，提高了计算效率，保证了搜索能力。开发阶段模拟海星的捕食和再生行为，采用双向搜索策略和特殊的运动方式，保证了开发过程的收敛性。

(1)初始化阶段

在SFOA的初始化阶段，海星的位置在设计变量的边界之间随机生成，可以表示为矩阵：－

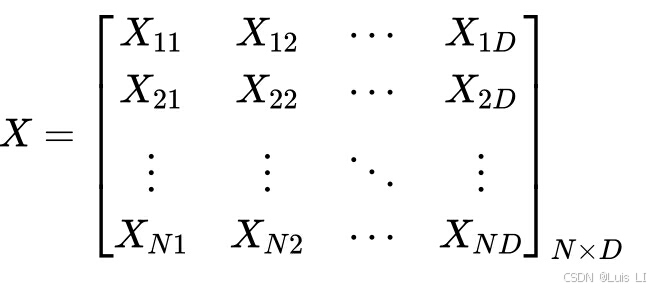
其中X是保存大小为N × D的海星位置的矩阵，N是种群大小，D是设计变量的维数。在初始化阶段，每个海星在方程中的位置被定义为：

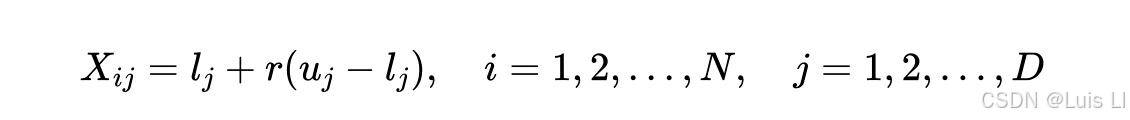
其中Xij表示第i个海星的第j维位置，r表示（0，1）之间的随机数，uj和lj分别是第j维设计变量的上界和下界。在生成初始化的位置矩阵之后，可以通过从目标函数评估来获得所有海星的适应度值，该目标函数也可以存储为向量：

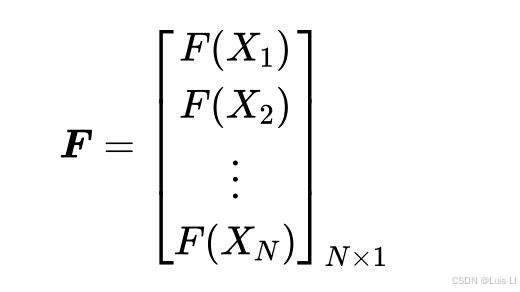
其中F是存储和更新所获得的适应度值的矩阵，大小为N × 1。初始化完成后，SFOA进入主循环，进入探索和开发阶段。

(2)勘探阶段

为了模拟海星的探索行为，在SFOA算法中建立了探索阶段，模拟海星的五条手臂的搜索能力，其中眼睛嵌入在手臂的末端，如图所示。在SFOA的探索阶段，提出了一种新的搜索模式，将D＞5的五维搜索模式和 的一维搜索模式结合起来，用于不同的优化问题。以海星的五臂为尺度阈值

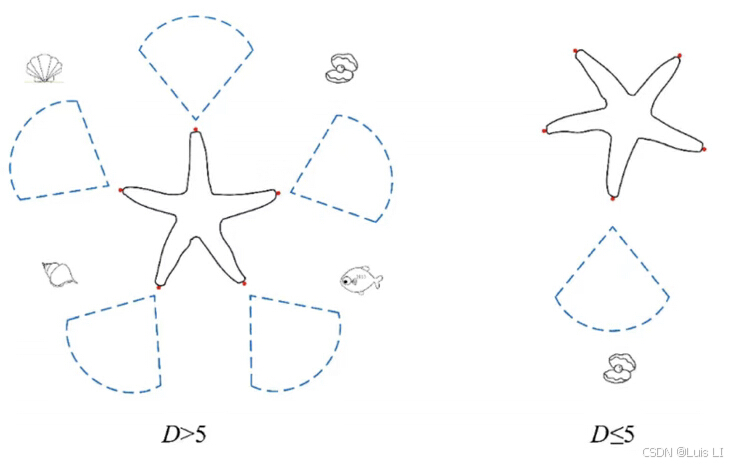
如果优化问题的维数大于5，则该问题的搜索空间很广，需要海星移动所有五只手臂来探索周围的环境。此外，海星的手臂需要搜索代理中最佳位置的知识来引导它们的运动。因此，本文建立了这一阶段的数学模型 ．

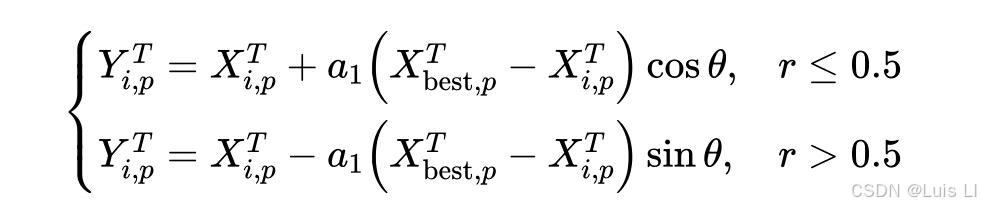
 其中YT i;p和XT i;p分别表示海星的获得位置和当前位置。XT best;p表示当前最佳位置的p维，p是D维中随机选择的五个维，a1和h计算如下：

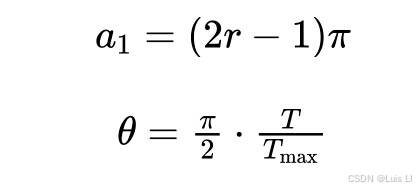
其中T是当前迭代，Tmax表示最大迭代。正弦和余弦项表示海星的手臂可以向左或向右扭转以相同的概率接近食物。在探索阶段，a1是为每个候选和迭代中的更新位置随机生成的，并且h随着迭代次数而变化。

对于优化问题中的D＞5的情况，当更新的位置在设计变量的边界之外时，手臂有保持在先前位置而不是移动到更新的位置的趋势。上述内容可以表示为：

其中p表示更新的尺寸，lb和ub分别表示设计变量的界限。

如果优化问题的维数不大于5，则探索阶段使用一维搜索模式来更新位置。在这种情况下，海星中只有一只手臂移动以利用来自其他海星的位置信息来搜索食物源。更新后的位置可以建立为：

其中，h与前面的更新规则类似，如果获得的海星位置超出边界，海星倾向于停留在先前的位置，而不是移动到更新的位置。

(3)开发阶段

SFOA在开发阶段考虑了捕食和更新行为，并设计了两种更新策略。为了对海星的捕食阶段进行建模，SFOA采用并行双向搜索策略，该策略需要利用其他海星的信息以及种群当前的最佳位置。首先计算最佳位置与其他海星之间的五个距离，然后随机选择两个距离作为确认更新每个海星的位置，利用并行双向搜索策略。距离可以计算为：

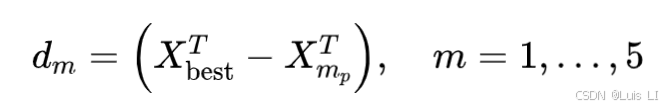
 其中dm是全局最佳和其它海星之间的五个获得的距离，而mp是五个随机选择的海星。因此，每个海星在捕食行为中的更新规则被建模为：

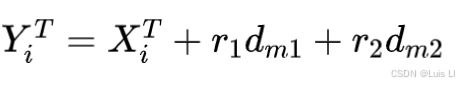
 其中，r1和r2是（0，1）之间的随机数，而dm1和dm2是在dm中随机选择的。海星的捕食行为如图所示。基于并行的双向搜索策略，在同一迭代中，海星的候选解向较好的引导解方向移动，而其他候选解则向后移动。因此，候选者具有相同的能力来克服局部最优。

 此外，海星在捕食过程中，由于其缓慢的运动，容易受到其他捕食者的攻击。如果捕食者捕获海星，海星可能会被切断并失去一只手臂以逃避捕获。因此，SFOA的再生阶段仅在种群中的最后一个海星中实施（i = N）。由于再生阶段需要几个月的生命，海星的移动速度非常缓慢。因此，我们在再生阶段对更新规则进行建模，并且位置通过以下方式更新：

 其中，T是当前迭代，Tmax表示最大迭代次数，N是群体大小。如果在设计变量的边界之外，可以将位置设置为：

 再生阶段如下图所述。尽管再生阶段在开发阶段中嵌入了非常少的函数求值，但该阶段对于避免局部解和增强全局收敛性是必要的。

 如前所述，SFOA包括初始化、探索和开发阶段。为了实现SFOA，探索和开发阶段在主循环中彼此并行，而适应度值在更新每个阶段的位置后计算。停止准则由最大迭代确定。一旦完成，SFOA输出全局解和收敛曲线。

function [xposbest,fvalbest,Curve] = SFOA(Npop,Max_it,lb,ub,nD,fobj)
% Starfish optimization algorithm (SFOA)
% Created by Dr. Changting Zhong (Email: zhongct@hainanu.edu.cn)
% Paper: Changting Zhong, Gang Li, Zeng Meng, Haijiang Li, Ali Riza Yildiz, Seyedali Mirjalili. 
% Starfish Optimization Algorithm (SFOA): A bio-inspired metaheuristic algorithm for global optimization compared with 100 optimizers
% Neural Computing and Applications, 2024, accepted

%% Initialization
GP=0.5;     % parameter 

if size(ub,2) == 1
    lb = lb*ones(1,nD); ub = ub*ones(1,nD);
end

fvalbest = inf;
Curve = zeros(1,Max_it);
Xpos = rand(Npop,nD).*(ub-lb)+lb;
for i = 1:Npop
    Fitness(i) = feval(fobj,Xpos(i,:));
end
[fvalbest,order] = min(Fitness);    % global best fitness
xposbest = Xpos(order,:);        % global best position

newX = zeros(Npop,nD);
%% Evolution
T = 1;
while T <= Max_it
    theta = pi/2*T./Max_it;
    tEO = (Max_it-T)/Max_it*cos(theta);
    if rand < GP %  exploration of starfish
        for i = 1:Npop
            if nD > 5
                % for nD is larger than 5
                jp1 = randperm(nD,5);
                for j = 1:5
                    pm = (2*rand-1)*pi;
                    if rand < GP
                        newX(i,jp1(j)) = Xpos(i,jp1(j)) + pm*(xposbest(jp1(j))-Xpos(i,jp1(j)))*cos(theta);
                    else
                        newX(i,jp1(j)) = Xpos(i,jp1(j)) - pm*(xposbest(jp1(j))-Xpos(i,jp1(j)))*sin(theta);
                    end
                    if newX(i,jp1(j))>ub(jp1(j)) || newX(i,jp1(j))<lb(jp1(j))
                        newX(i,jp1(j)) = Xpos(i,jp1(j));
                    end
                end
            else
                % for nD is not larger than 5
                jp2 = ceil(nD*rand);
                im = randperm(Npop);
                rand1 = 2*rand-1;
                rand2 = 2*rand-1;
                newX(i,jp2) = tEO*Xpos(i,jp2) + rand1*(Xpos(im(1),jp2)-Xpos(i,jp2))+rand2*(Xpos(im(2),jp2)-Xpos(i,jp2));
                if newX(i,jp2)>ub(jp2) || newX(i,jp2)<lb(jp2)
                    newX(i,jp2) = Xpos(i,jp2);
                end  
            end
            newX(i,:) = max(min(newX(i,:),ub),lb);  % boundary check
        end
    else % exploitation of starfish
        df = randperm(Npop,5);
        dm(1,:) = xposbest - Xpos(df(1),:);
        dm(2,:) = xposbest - Xpos(df(2),:);
        dm(3,:) = xposbest - Xpos(df(3),:);
        dm(4,:) = xposbest - Xpos(df(4),:);
        dm(5,:) = xposbest - Xpos(df(5),:);  % five arms of starfish
        for i = 1:Npop
            r1 = rand; r2 = rand;
            kp = randperm(length(df),2);
            newX(i,:) = Xpos(i,:) + r1*dm(kp(1),:) + r2*dm(kp(2),:);   % exploitation
            if i == Npop
                newX(i,:) = exp(-T*Npop/Max_it).*Xpos(i,:);  % regeneration of starfish
            end
            newX(i,:) = max(min(newX(i,:),ub),lb);  % boundary check
        end
    end
    
    % Fitness evaluation
    for i = 1:Npop
        newFit = feval(fobj,newX(i,:));
        if newFit < Fitness(i)
            Fitness(i) = newFit;
            Xpos(i,:) = newX(i,:);
            if newFit < fvalbest
                fvalbest = Fitness(i);
                xposbest = Xpos(i,:);
            end
        end
    end
    
    Curve(T) = fvalbest;
    T = T+1;
end