从原理浮点数的四舍五入问题

在某一天的刷题中，偶然写道了这道题

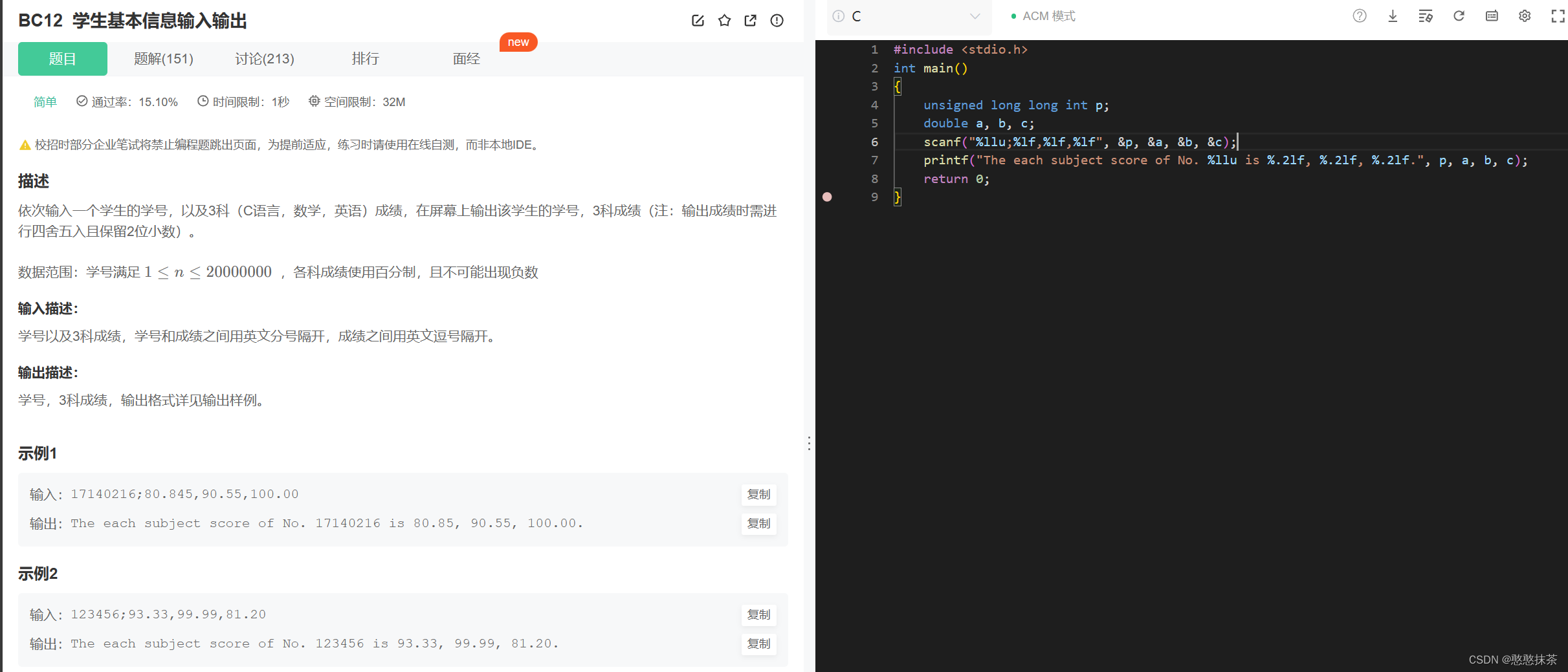
写完以后发现没有满分，由此引发了猜想，对于编译器运行时使用

printf("%.1f",3.155);

其它本身就会进行四舍五入所以会出现以下运行结果

---

---

但如果我们保留两位小数呢？

啊，不该是输出3.16么？为什么是3.15呢？

---

我们带着疑问对a进行监视

原来如此，a在存储时不是存的3.155，而是3.15499997，那么自然保留两位小数就是3.15了嘛；

---

为什么会有误差呢？

原因如下

浮点数在计算机中存储时，小数部分也是按二进制存储的；例如：0.9 十进制转换为二进制是：0.111001100110011001100…无限循环而计算机中存储的位数是有限的，因此当变量存储不了后面的二进制小数时，再转换回十进制就产生误差了float: 单精度浮点数 十进制保存7位置，二进制保存23位0.111001100110011001100…转换回十进制就是：0.89999998。double: 双精度浮点_浮点数由于存储空间不够引起的截断误差

---

回归本题（链接：学生基本信息输入输出_牛客题霸_牛客网 (nowcoder.com)）

浮点数储存原理：

 针对于与float类型的浮点数，我们知道其大小为四个字节

然而对于数学的科学计数法来说如果对于有个小数，比如0.05；针对于科学计数法来说，我们一般不按照他为0.05来说，而是按照（-1）^0*5.0x10^(-2)；来说，那么计算机总不能直接来按照0.05来存储吧，毕竟我根据上面的验证，也大致得知了，存储的时候可能无法精准的进行存储，而是存储一个非常接近的数字，无限接近的数，所以计算机就是按照科学计数法的方法进行存储浮点数的

而0.05，同样对于0.06，我们通过科学计数法表示就为（-1）^0*6.0x10^(-2)；所以对于0.05，我们只需要存储该数的重要部分便可以，也就是  0   5.0    -2。至于后续怎么保存，我们就需要查找了。

但是又回过来了，我们都知道计算机存储的时候不是以十进制存储，而是以二进制方法存储到文件，以二进制读取，后转化为十六进制进行显示，

那么大致原理便知道了

那么对于这四个数，每一部分都是位于不同位置，所以存储的时候也尤其对应的位置

比如，国际标准IEEE（电气和电子工程协会）754中就有相关规定

所以0.05的存储方法便知道了

小插曲如何将十进制小数转化为二进制表示：

首先

• 0.05 的二进制表示为：0.0000110011001100110011001100110011001100110011001101...（无限循环）。

但是根据前面监测查看实际内存存储情况来看，其实并不会将一个小数精准保存，而是保存一个非常接近的数，所以那0.05为例，他的二进制表示在计算机看来并不会使用0.0000110011001100110011001100110011001100110011001101...（无限循环）来表示的而是进行小数位后面一些不必要的取舍，对于取舍多少位是由用户存的为float还是double。

对于此

所以0.05如果为float那么他的二进制用科学计数法表示为：1.10011001100110011001101 × 2^(-5)。

• 所以IEEE 754 单精度浮点数表示：

  • 符号位（S）：0（因为0.05是正数）。

  • 指数位（E）：实际指数为-5。

  • 尾数位（M）：1.10011001100110011001101 的小数部分是10011001100110011001101，取前23位。

 s=0    M=1.10011001100110011001101    E=-5

那么话又回过来了，0.05实际上的S位与M位就是存的为

0  ？？？？？？？？  10011001100110011001101

E为一个负数，但在IEEE754规定E为一个无符号的整数，那么到底怎么存的呢？

IEEE754规定：

所以E其实存的是-5+127=122；123二进制表示为01111010

所以二进制存储为：

0  01111010  10011001100110011001101

---

温馨提示 

 并不是所有的浮点数都不能精确的进行存储，只是有的部分浮点数不能比如3.14都可以，但是0.1都不可以，如果想要验证的话可以自己尝试一下，可以通过在vs的调试很简单的验证。

---

---

存储原理就是以上，说完了以后那么我们就知道为什么要+0.005，为什么有时候又不需要加了 。

那么保留两位小数，我们直接在加0.005就可以了嘛

#include <stdio.h>
int main() 
{
	unsigned long long int p;
    double a, b, c;
    scanf("%llu;%lf,%lf,%lf", &p, &a, &b, &c);
	if(a!=0)
	a = a + 0.0005;
	if(b!=0)
	b = b + 0.0005;
	if(c!=0)
	c = c + 0.0005;
    printf("The each subject score of No. %llu is %.2lf, %.2lf, %.2lf.", p, a, b, c);
    return 0;
}

成功！！！