检查与处理缺失值、标准化数据、数据可视化

检查与处理缺失值

有时数据中的某个或某些特征的值是不完整的，这些值称为缺失值。pandas提供了识别缺失值的isnull()方法和识别非缺失值的notnull()方法，这两种方法在使用时返回的都是布尔值，即True和 False。结合sum 函数、isnull()方法和notnul1()方法，可以检测数据中缺失值的分布以及数据中一共含有多少缺失值。

引入pandas和numpy库，操作如下：

import pandas as pd
import numpy as np

输入pandas和numpy库这两个库完后，点击运行。

用read_excel引入电商用户行为分析数据文件

data=pd.read_excel('E:/hql/mongo hql/Python hql/电商用户行为分析数据.xlsx',sheet_name='user_info')

用data查看头两行的数据，然后点击运行，操作如下

data.head(2)

sum()函数和mode()函数、isnull()方法

用sum()函数查询缺失值的数目

data.isnull().sum()

用mode()函数查询缺失值的数目

data['device'].mode()

data[data['device']=='mobile']['operative_system'].mode()

分布处理：如果设备和系统同时缺失的，就用mobile和ios去填充，如果只缺失了系统的，那么就再根据他的设备去填充
 

data[data['operative_system']=='iOS']['device'].fillna('mobile',inplace=True)

data.dropna(how='any')
data.info()

这样就完成了缺失值的处理。

制作标准化数据

1、引入pandas和numpy库，操作如下：

import pandas as pd
import numpy as np

输入pandas和numpy库这两个库完后，点击运行，如图所示：

运行完后，下面没有报红那就说明引入成功了，如果有报红那就查看自己是不是拼写错误。

2、用read_csv引入user_pay_info文件

data=pd.read_csv('E:/hql/mongo hql/Python hql/user_pay_info.csv')

用data查看头两行的数据，然后点击运行，操作如下

data.head(2)

3、写一个离差标准化的函数

def min_max_scale(data):
    data=(data-data.min())/(data.max()-data.min())
    return data

查看头五行数据

data['每月支出离差标准化']=min_max_scale(data['每月支出'])
data.head(5)

4、做标准差标准化

先按照公式，写一个标准化函数

def standard_scale(data):
    data=(data-data.mean())/data.std()
    return data

5、对每月支出进行标准差标准化处理

data['每月支出标准差标准化']=standard_scale(data['每月支出'])
data.head(2)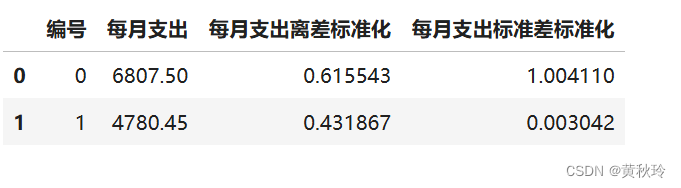

6、小数定标标准化，直接除以你的量级，消除量级影响，让数据处于-1到1之间

def decimal_scale(data):
    data=data/10**np.ceil(np.log10(data.abs().max()))
    return data

data['每月支出小数定标标准化']=decimal_scale(data['每月支出'])
data.head(2)

这样我们就完成标准化数据的操作了。

数据可视化

若使用Matplotlib库进行图形的绘制，则需要先了解pyplot模块的基础语法及其动态的rc参数的设置。大部分的pyplot图形绘制都遵循一个流程,这个流程主要分为3个部分。

1.掌握 pyplot 基础语法    

掌握pyplot模块的基础语法的使用，可从创建画布与创建子图、添加画布内容、保存与显示图形3个部分进行。

(1)创建画布与创建子图

第一部分的主要作用是构建出一张空白的画布，可以选择是否将整个画布划分为多个部分，方便在同一个图上绘制多个图形。当只需要绘制一个简单的图形时，这部分内容可以省略。在pyplot中,创建画布与创建并选中子图的常用函数/方法及其作用如表所示，为了方便读者查看，将matplotlib.pyplot模块简写为 plt。

(2)添加画布内容  

 第二部分是绘图的主体部分。其中的添加标题、添加坐标轴标签、绘制图形等步骤是没有先后顺序的，可以先绘制图形，也可以先添加各类标签。但是添加图例一定要在绘制图形之后。在pyplot中添加各类标签和图例的常用函数及其作用如表所示。

(3)保存与显示图形

第三部分主要用于保存和显示图形，这部分内容的常用函数只有两个，并且参数很少，如表所示。

引入库

import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']='SimHei'
plt.rcParams['axes.unicode_minus']=True
# %matplotlib inline

处理数据

data=np.load('E:/hql/mongo hql/Python hql/2001-2019年劳动力与就业人员数据.npz',encoding='ASCII',allow_pickle=True)
data

线形图

显示图中的中文字体

plt.rcParams['font.sans-serif']='SimHei

设置标题

plt.title('第一张线形图')

设置x轴标签

plt.xlabel('x轴的标签')

设置y轴标签

plt.ylabel('y轴的标签')

设置x轴的范围

plt.xlim(0,1)

设置y轴的范围

plt.ylim(0,1)

规定x轴刻度

plt.xticks([0,0.2,0.4,0.6,0.8,1])

规定y轴刻度

plt.yticks([0,0.2,0.4,0.6,0.8,1])

添加y=x^2曲线

plt.plot(data,data**2)

添加y=x^4曲线

plt.plot(data,data**4)

添加图例

plt.legend(['y=x^2','y=x^4'])

设置图片保存路径

plt.savefig('E:/hql/mongo hql/Python hql/第一张线形图')

输入show（）显示线形图

plt.show()

尝试在同一画布中，同时画两个图
 

#准备数据
x=np.arange(0,np.pi*2,0.01)

plt.rcParams['axes.unicode_minus']=True
#准备画布
pl=plt.figure(figsize=(8,6),dpi=80)
#画第一张子图
ax1=pl.add_subplot(2,1,1)
plt.title('第一张线形图')#设置标题
plt.xlabel('x轴的标签')#设置x轴标签
plt.ylabel('y轴的标签')#设置y轴标签
plt.xlim(0,1)#设置x轴的范围
plt.ylim(0,1)#设置y轴的范围
plt.xticks([0,0.2,0.4,0.6,0.8,1])#规定x轴刻度
plt.yticks([0,0.2,0.4,0.6,0.8,1])#规定y轴刻度
plt.plot(data,data**2)#添加y=x^2曲线
plt.plot(data,data**4)#添加y=x^4曲线
plt.legend(['y=x^2','y=x^4'])#添加图例

画第二张图

plt.rcParams['lines.linestyle']='-.'
plt.rcParams['axes.unicode_minus']=False
ax2=pl.add_subplot(2,1,2)
plt.title('第二张图')
plt.xlabel('x')
plt.ylabel('y')
plt.xlim(0,np.pi*2)
plt.ylim(-1,1)
plt.xticks([0,np.pi/2,np.pi,np.pi*1.5,np.pi*2])
plt.yticks([-1,-0.5,0,0.5,1])
plt.plot(x,np.sin(x))
plt.plot(x,np.cos(x))
plt.legend(['y=sin(x)','y=cos(x)'])
plt.savefig('E:/hql/mongo hql/Python hql/第二张线形图')
plt.show()

绘制散点图

散点图(Scatter Diagram)又称为散点分布图，是以一个特征为横坐标，以另一个特征为纵坐标，利用坐标点(散点)的分布形态反映这两个特征间的统计关系的一种图形。值由点在图形中的位置表示，类别由图形中的不同标记表示，通常用于比较跨类别的数据。

散点图可以提供两类关键信息，具体内容如下：

(1)特征之间是否存在数值或数量的关联趋势，关联趋势是线性的还是非线性的。

(2)如果某一个点或某几个点偏离大多数点，那么这些点就是离群值，通过散点图可以一目了然，从而可以进一步分析这些离群值是否在建模分析中产生较大的影响。

散点图可通过散点的疏密程度和变化趋势表示两个特征的数量关系。如果有3个特征，且其中一个特征为类别型特征，散点图可改变该特征的点的形状或颜色，即可了解两个数值型特征和这个类别型特征之间的关系。

scatter 函数的常用参数及其说明如表所示。

某公司经调查整理得到就业人员数据，其中记录了2001年-2019年的就业人员数量。为了进一步分析各年度劳动力人数、城镇就业人数和乡村就业人数等情况，需要通过可视化图形进行展示分析。2001年-2019年劳动力与就业人员数据的特征说明如表所示。

绘制2001年-2019年劳动力人数散点图

plt.figure(figsize=(12,6),dpi=1080)
plt.xlabel('年份(年)')
plt.ylabel('劳动力人数(万人)')
plt.ylim(70000,85000)
plt.xticks(range(2001,2020,1),labels=values[:,0])
plt.title('2001-2019年劳动力人数散点图')
plt.scatter(values[:,0],values[:,1],marker='o')
plt.show()

准备开始画第二个散点图

plt.figure(figsize=(12,6),dpi=1080)
plt.xlabel('年份(年)')
plt.ylabel('劳动力人数(万人)')
plt.xticks(range(2001,2020,1),labels=values[:,0])
plt.title('2001-2019年劳动力人数散点图')
plt.scatter(values[:,0],values[:,3],marker='D',c='r',alpha=0.5)
plt.scatter(values[:,0],values[:,4],marker='o',c='y',alpha=0.8)
plt.legend(['城镇就业人口','乡村就业人口'])
plt.show()

绘制折线图

折线图(Line Chart)是一种将数据点按照顺序连接起来的图形，可以看作将散点图按照x轴坐标顺序连接起来的图形。折线图的主要功能是查看因变量y随着自变量x改变的趋势，适合用于显示随时间(根据常用比例设置)而变化的连续数据，同时还可以显示数量的差异和增长趋势的变化。

plot 函数在官方文档的语法中只要求输入不定长参数，实际可以输入的参数主要如表所示。

color参数的8种常用颜色的缩写如表所示

绘制2001年-2019年劳动力人数折线图

plt.figure(figsize=(12,6),dpi=1080)
plt.xlabel('年份(年)')
plt.ylabel('劳动力人数(万人)')
plt.ylim(70000,85000)
plt.xticks(range(2001,2020,1),labels=values[:,0])
plt.title('2001-2019年劳动力人数散点图')
plt.plot(values[:,0],values[:,2],linestyle='-',marker='D',c='r')
plt.legend(['城镇就业人口','乡村就业人口'])
plt.show()

对第二张折线图添加两条折线

plt.figure(figsize=(12,6),dpi=1080)
plt.xlabel('年份(年)')
plt.ylabel('劳动力人数(万人)')
plt.xticks(range(2001,2020,1),labels=values[:,0])
plt.title('2001-2019年劳动力人数散点图')
plt.plot(values[:,0],values[:,3],marker='D',linestyle='-',c='r')
plt.plot(values[:,0],values[:,4],marker='o',linestyle='-',c='y')
plt.legend(['城镇就业人口','乡村就业人口'])
plt.show()

绘制柱形图

柱形图(Bar Chart)的核心思想是对比，常用于显示一段时间内的数据变化或显示各项数据之间的比较情况。柱形图的适用场合是二维数据集(每个数据点包括两个值x和y),但只有一个维度的值需要比较。例如，年销售额就是二维数据，即“年份”“销售额”，但只需要比较“销售额”这一个维度的数据。柱形图利用柱形的高度，反映数据的大小。人眼对柱形高度差异很敏感，辨识效果非常好。柱形图的局限在于它只适用于中小规模的数据集。

bar函数的常用参数及其说明如表所示。

绘制2019乡村就业人数柱状图

labels=['城镇就业人口','乡村就业人员']
plt.figure(figsize=(6,6),dpi=1080)
plt.xlabel('类别')
plt.ylabel('人数（万人）')
plt.xticks(range(2),labels)
plt.title('2019乡村就业人数柱状图')
plt.bar(range(2),values[-1,3:5],width=0.5,color=['r','b'],alpha=0.6)#alpha颜色饱和度
plt.show()

绘制饼图

饼图(PieGraph)将各项数据的大小与各项数据总和的比例显示在一张“饼”中，以“饼块”的大小来确定每一项数据的占比。饼图可以比较清楚地反映出部分与部分、部分与整体之间的比例关系，易于显示每组数据相对于总数的比例，而且显示方式直观。

pie 函数的常用参数及其说明如表示

绘制2019年城乡就业人数分布饼图

labels=['城镇就业人口','乡村就业人员']
explode=[0.01,0.01]
plt.figure(figsize=(6,6),dpi=100)
plt.pie(values[-1,3:5],explode=explode,labels=labels,autopct='%1.1f%%',startangle=90,colors=['r','y'],shadow=True,radius=0.8)
plt.title('2019年城乡就业人数分布饼图')
plt.savefig('E:/hql/mongo hql/Python hql/饼图')
plt.show()

绘制箱线图

箱线图(Boxplot)也称箱须图，其绘制时，需使用常用的统计量，便能提供有关数据位置和分散情况的关键信息，尤其在比较不同特征时，可表现出这些特征的分散程度差异。如图标出了箱线图中每条线表示的含义。

箱线图利用数据中的5个统计量(非异常值的下边缘、下四分位数、中位数、上四分位数和非异常值的上边缘)来描述数据。它也可以粗略地看出数据是否具有对称性、分布的分散程度等信息，特别是可以用于对多个样本进行比较。

boxplot函数的常用参数及其说明如表所示。

绘制2001年-2019年城乡就业人数分布箱线图

#准备画箱线图
labels=['城镇就业人口','乡村就业人员']
gdp=(list(values[:,3]),list(values[:,4]))
gdp

p=plt.figure(figsize=(6,6),dpi=100)
plt.boxplot(gdp,notch=True,labels=labels,meanline=True)
plt.title('2001年-2019年城乡就业人数分布箱线图')
plt.savefig('E:/hql/mongo hql/Python hql/箱线图')
plt.show()

这样我们就全部完成了数据可视化的操作了。