图论基础与遍历算法

图的逻辑结构及其实现

图是由节点和边构成的，边分为有向边和无向边，对应有向图和无向图，逻辑结构如下：

根据这个逻辑结构，我们可以实现每个节点：

 //节点需要存储自身的值，也需要存储与其邻接的节点
 struct Vertex{
     int val; //自身值
     vector<Vertex*> neighbors; //用vector(动态容器)存储指向邻接节点的指针
 }

你有没有发现，这和我们之前实现多叉树简直一模一样：

 strcut Treenode{
     int val;
     vetcor<Vertex*> neighbors;
 }

所以，图本质上是高级一点的多叉树而已，适用于树的DFS(深度优先搜索)/BFS(广度优先搜索)全部适用于图。

我们知道，多叉树的存储直接适用节点和指针进行存储就好了，遍历是从根节点开始遍历。那图怎么存呢？图是不存在根节点这个概念的。

邻接表和邻接矩阵

相当于每个节点都是根节点，我们用邻接表和邻接矩阵来实现图。

比如还得刚才那幅图：

用邻接表和邻接矩阵的存储方式如下：

邻接表很直观，我们把节点x的所以邻居存到一个列表里，然后把x和这个列表关联起来（一般的x节点中建立一个指针，指向这个列表），这样就可以通过节点x找到它的所有邻接节点。

邻接矩阵是一个二维布尔数组，我们权且称为matrix，如果节点Vertex(i)与Vertex(j)有关联，那么就把matrix[i][j]设为True

(上图中绿色的格子代表有关联)，如果想知道节点Vertex(i)的所有邻接节点，去扫一圈matrix[i][....]就行了。

 //邻接表
 vector<int> graph[]; //用数据类型为vector<int>的数组来存储邻接节点
 ​
 //邻接矩阵 matrix[x][y]记录是否有一条x指向y的边
 bool graph[][];

那么，这两种存储图的方式各有什么优劣呢？

邻接表的好处就是占用的空间少，我们看上面邻接矩阵的图，有很多非绿色部分，这些部分都是没有被利用上的。反观邻接表，开辟出来的所有vector空间都被利用上了。坏处是邻接表不能快速判断两个节点之间是否关联，同样，先看邻接矩阵，如果我们要判断节点x与节点y是否有关联，只需要判断graph[x][y]是否为True就好了。而邻接表想要判断x是否与y有关联，则需要遍历graph[x]查看是否有y存在，如果有，才能说明x有一条指向y的边。

所以，使用哪一种方式实现图，要看具体情况。

在常规的算法题中，邻接表的使用会更频繁一些，主要是因为操作起来比较简单，空间利用度高。但是邻接矩阵也不能忽视，遇到需要快速判断两个节点是否有关联的场景，使用邻接矩阵会大幅降低时间复杂度，同时一些隐晦性质可以借助精妙的矩阵运算展现出来。

度

最后，我们再明确一下图特有的【度(degree)】的概念，在无向图中，【度】就是每个节点相连的边的条数。

由于有向图有方向，所以有向图的每个节点的【度】被细分为【入度】和【出度】。

在基础图的基础上继续扩展出【有向加权图】、【无向加权图】等复杂图

有向加权图怎么实现，很简单：

我们在存储节点时，不仅存储当前节点的所有邻接节点，还要存储这个节点到每个邻接节点的权重即可。

如果是邻接矩阵，那就把matrix[x][y]的值改为x指向y边的权重即可，0表示没有连接。

实现代码如下：

 //有向有权图的邻接表
 vector< pair<int,int> > graph[] // pair[0]代表邻接节点的下标值,pair[1]代表指向邻接节点的
     
 //有向有权图的邻接矩阵
 int graph[][];
 //如果不能提前知道图中节点的个数，就用动态vector
 vector<vector<int>> graph;

图的遍历

之前在学习数据结构和算法的框架思维中说过，各种数据结构被发明出来无非就是为了遍历和访问，【遍历】是所有数据结构的基础。

图的逻辑结构和多叉树比较类似，所以图的遍历我们参考多叉树的遍历，多叉树遍历框架如下：

 void traverse(TreeNode* root){
     if(root == nullptr) return;
     //前序位置
     for(TreeNode* child : root->children){
         traverse(child);
     }
     //后序位置
 }

但是，图结构中可能有环存在，当图不是连通图时。这时图被分为好几个连通族。简单来说，你从图中的某一个节点开始遍历，有可能走了一圈又回到了这个节点【此时我们只在其中的一个连通族进行了遍历，其他连通族和第一个遍历所在节点的连通族无节点相连，我们遍历不过去】，而树不会这样，树从根节点开始遍历，最后一定会遍历到叶子节点，绝不可能回到它自身。

所以，如果图包含环【即图不是连通图，存在好几个连通族】，我们就需要借助visited[](记录节点是否被遍历过)数组进行辅助：

 //记录被遍历过的节点
 vector<bool> visited;   //如果已知图中所有节点个数n，则直接声明 vector<bool> visited[n];
 //记录从起点到当前节点的路径
 vector<bool> onPath;    //路径上的节点改为true即可
 ​
 //图的遍历框架
 void traverse(Graph graph,int s){   //注意：遍历图的时候要注意图是怎么存储的？是用邻接表存的还是邻接矩阵存的
     //如果已经遍历过了，则跳过（不走回头路）
     if(visited[s]) return;
     //经过节点s，标记为已遍历
     visited[s] = true;
     //做选择：标记节点s在路径上
     onPath[s] = true;
     
     //BFS 深度遍历
     for(int neighbor:graph.neighbors(s)){ 
         traverse(graph,neighbor); 
     }
     //撤销选择:节点s离开路径
     onPath[s] = false;
 }

注意visited[]和onPath[]的区别，因为二叉树算是特殊的图【连通图】，所以用二叉树的遍历过程来理解这两个数组的区别：

上述gif描述了递归变量二叉树的过程，在visited中被标记为true的节点用灰色表示，在onPath中被标记为true的节点用绿色表示。类比贪吃蛇游戏，visited记录蛇走过的格子，onPath记录蛇身。在图的遍历过程中，onPath可以用来判断是否成环，类似与贪吃蛇是否自己咬到自己。这下你能清楚理解visited与onPath的区别了吧。

成环检测

onPath[]如何判断图中是否含有环呢？拿贪吃蛇游戏作为例子，图中有环就代表着贪吃蛇自己咬到自己了。也就是说遍历到某个节点时，其所有邻接节点全在onPath[]中，这时候再往记录路径中加入节点，会出现一个被记录两次的节点，这个节点就是连成环的关键节点。

一般我们在处理路径相关的问题中，这个onPath[]是一定会被用到的，比如拓扑排序。

另外，我们注意到，onPath[]的两步操作【做选择，撤销选择】在之前的文章【回溯/BFS/动态规划 核心框架】中提到过。onPath[]的两步操作是在遍历的for循环之外进行的。和BFS核心框架一模一样，也就是说，onPath[]只关注节点本身，并不关注节点之间的连接。

回顾一下回溯/BFS/动态规划核心框架

回溯框架关注节点与节点之间的连接，也就是树枝

.....
 //遍历下一层
 for(Node child : root->children){
     //做选择
     ......
     traverse(child);
     //撤销选择
     ......
 }

BFS关注节点本身，每次都需要进入节点

 .....
 //做选择
 ......
 //遍历下一层
 for(Node child : root->children){
     traverse(child);
 }
 //撤销选择
 ......

动态规划框架就是关注整个子树，框架代码这里就不给出了。

所以对于图的遍历，我们常用的算法是DFS与BFS算法。

说了这么多onPath[],我们再讨论下visited[]，其目的很明显了，由于图可能含有环，visited就是防止递归重复遍历同一个节点从而进入死循环。

如果问题显然不含环，就没必要使用visited[]了。

题目实践

LeetCode 797 所有可能

---

给你一个有 n 个节点的 有向无环图（DAG），请你找出所有从节点 0 到节点 n-1 的路径并输出（不要求按特定顺序）

graph[i] 是一个从节点 i 可以访问的所有节点的列表（即从节点 i 到节点 graph[i][j]存在一条有向边）。

示例 1：

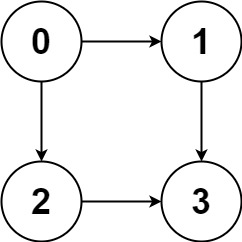
 输入：graph = [[1,2],[3],[3],[]]
 输出：[[0,1,3],[0,2,3]]
 解释：有两条路径 0 -> 1 -> 3 和 0 -> 2 -> 3

示例 2：

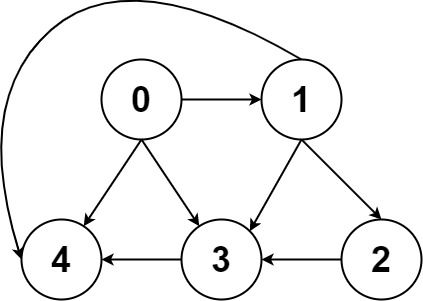
 输入：graph = [[4,3,1],[3,2,4],[3],[4],[]]
 输出：[[0,4],[0,3,4],[0,1,3,4],[0,1,2,3,4],[0,1,4]]

提示：

• n == graph.length

• 2 <= n <= 15

• 0 <= graph[i][j] < n

• graph[i][j] != i（即不存在自环）

• graph[i] 中的所有元素 互不相同

• 保证输入为 有向无环图（DAG）

---

解题思路：

这道题很简单嘛，我们直接利用DFS遍历这个图。以 0 为起点遍历这个图，同时利用onPath[]记录走过的路径，遍历到终点时将路径加入到存储结果的result中即可。

解题代码：

 class Solution {
 public:
     vector <vector<int>> result; //存放结果
     vector<int> onPath; //记录当前路径  //在vector中查找的时间复杂度为o(n)
     vector <vector<int>> allPathsSourceTarget(vector <vector<int>> &graph) {
         dfs(graph, 0);
         return result;
     }
 ​
     void dfs(vector <vector<int>> &graph, int n) {
         //dfs终止条件
         if (n == graph.size() - 1) {
             onPath.push_back(n);
             result.push_back(onPath);
             onPath.pop_back();
             return;
         }
         //做出选择
         onPath.push_back(n);
         //进入下一层
         for (int i = 0; i < graph[n].size(); i++) {
             //遍历下一层
             dfs(graph, graph[n][i]);
         }
         //撤销选择
         onPath.pop_back();
     }
 };

最后总结一下，图的存储方式主要有邻接表和邻接矩阵两种，无论什么花里胡哨的图，都可以用这两种方式去存储。

与图相关还有很多有趣的算法：

1. 二分图判定

2. 环检测与拓扑排序

3. 最小生成树

4. Dijkstra最短路径算法

我们再看几道题：

LeetCode 133克隆图

给你无向 连通 图中一个节点的引用，请你返回该图的 深拷贝（克隆）。

图中的每个节点都包含它的值 val（int） 和其邻居的列表（list[Node]）。

 class Node {
     public int val;
     public List neighbors;
 }

测试用例格式：

简单起见，每个节点的值都和它的索引相同。例如，第一个节点值为 1（val = 1），第二个节点值为 2（val = 2），以此类推。该图在测试用例中使用邻接列表表示。

邻接列表 是用于表示有限图的无序列表的集合。每个列表都描述了图中节点的邻居集。

给定节点将始终是图中的第一个节点（值为 1）。你必须将 给定节点的拷贝 作为对克隆图的引用返回。

示例 1：

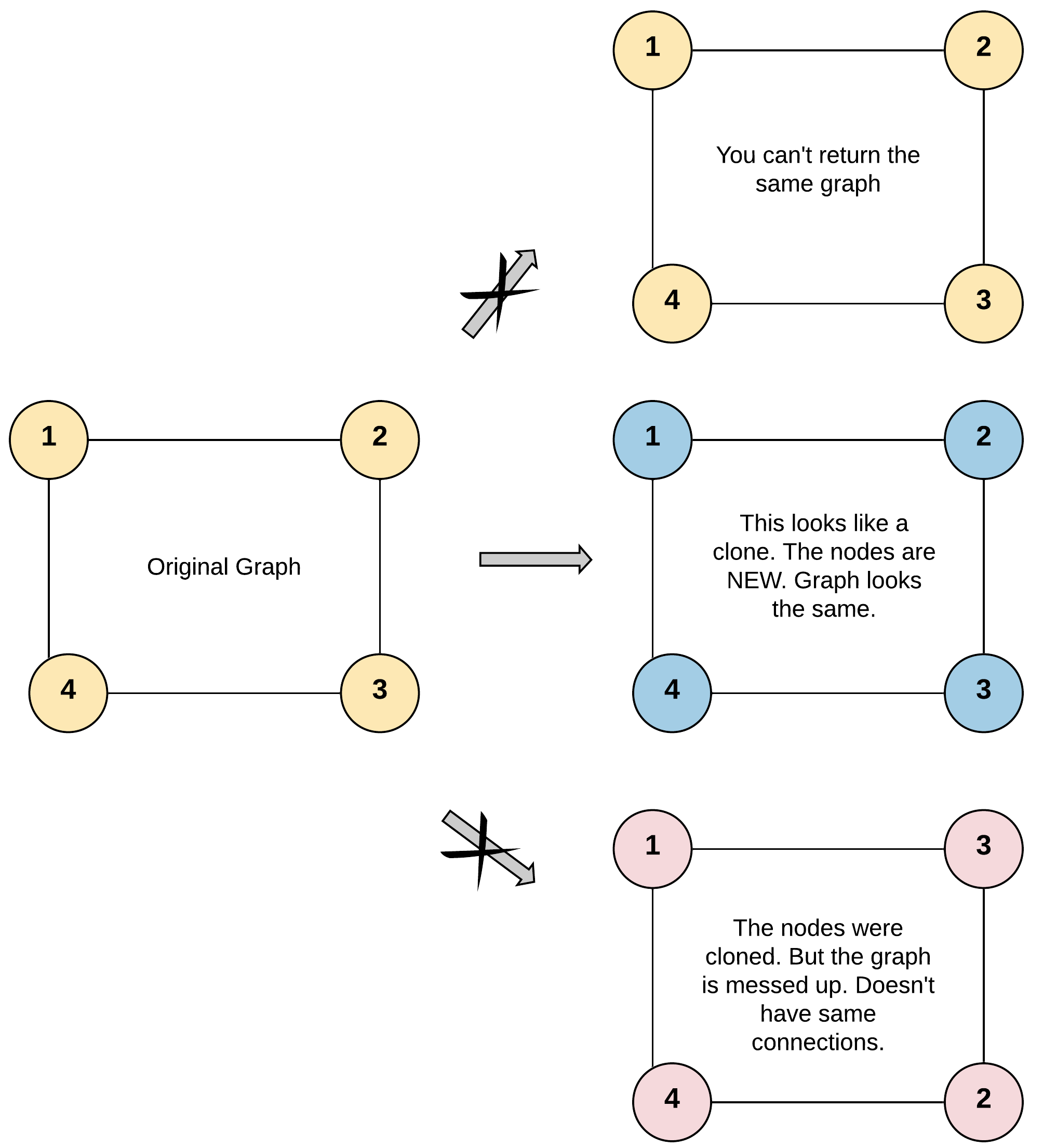
 输入：adjList = [[2,4],[1,3],[2,4],[1,3]]
 输出：[[2,4],[1,3],[2,4],[1,3]]
 解释：
 图中有 4 个节点。
 节点 1 的值是 1，它有两个邻居：节点 2 和 4 。
 节点 2 的值是 2，它有两个邻居：节点 1 和 3 。
 节点 3 的值是 3，它有两个邻居：节点 2 和 4 。
 节点 4 的值是 4，它有两个邻居：节点 1 和 3 。

示例 2：

 输入：adjList = [[]]
 输出：[[]]
 解释：输入包含一个空列表。该图仅仅只有一个值为 1 的节点，它没有任何邻居。

示例 3：

 输入：adjList = []
 输出：[]
 解释：这个图是空的，它不含任何节点。

提示：

• 这张图中的节点数在 [0, 100] 之间。

• 1 <= Node.val <= 100

• 每个节点值 Node.val 都是唯一的，

• 图中没有重复的边，也没有自环。

• 图是连通图，你可以从给定节点访问到所有节点。

Related Topics

深度优先搜索

广度优先搜索

图

哈希表

---

解题思路：

克隆图本质上就是在遍历图的基础上对每个节点进行深拷贝而已，一个节点只能被深拷贝一次，但却可以被观察到多次。

我提到了一个新名词“观察到”，和访问、遍历、以及深拷贝不同，“观察到”只是在遍历图中看到了节点，而这三个操作是看到了节点并且碰了节点，实实在在地进入了节点里面。

举个例子，我在遍历一个连通图时，我先遍历节点B，然后在节点B的所有邻居节点中选择一个最合适的节点进行遍历，这时候节点B有邻居节点A与节点C，我发现C才是我想到的下一节点，所以我进入节点C，不进入节点A。

在上述过程中，节点A被观察到，而节点C被遍历（访问）。

有些节点被观察到就可以立即遍历，有些节点观察到却不能被遍历，这是为什么呢？

很显然，每个节点只能被遍历一次，所以从来没有被遍历过的节点自然是一被观察到就立即被遍历，而遍历过的节点被观察到就只能跳过遍历咯。所以在遍历图的过程中，我们需要一个备忘录来辅助遍历，一般我们是用数组来作为备忘录记录节点是否被遍历，遇到 遍历过程中还需要遍历过的节点的部分元素 的情况，一般要考虑使用哈希表来作为备忘录。

有了以上这些知识储备，现在我们回到本题。刚刚说到了克隆图的本质：在遍历图的基础上对每个节点进行深拷贝，也就是说，遍历每个节点时，还需要创建一个深拷贝节点，并存储指向这个深拷贝节点的指针。

我们进一步分析，这个深拷贝节点不仅是拷贝了节点值，还要拷贝原来节点的所有邻接节点。怎么拷贝呢？按照遍历图的流程去看，我们深拷贝了某个节点以及此节点存储的值后，可以去观察它的所有邻接节点，如果邻接节点被访问过，我们就把备忘录中此邻接节点的拷贝节点的指针加入到此节点的邻接列表中，如果邻接节点没有被访问过，则直接递归到访问此邻接节点，进行同样的拷贝操作。

解题代码：

 //辅助备忘录，记录被访问过的节点
 unordered_map<Node*, Node*> visited;
 ​
 //采用DFS遍历方法
 Node* cloneGraph(Node* node){
     //判空
     if(node == nullptr){
         return node;
     }
     
     //查看是否在备忘录中
     if(visited.find(node) != visited.end()){ //在备忘录中
         return visited[node];
     }
     
     //不在备忘录中
     //拷贝节点
     Node* copyNode = new Node(node->val);
     visited[node] = copyNode;
     //拷贝列表
     for(auto& neighbor: node->neighbors){
         copyNode->neighbors.emplace_back(cloneGraph(node));
     }
     
     return copyNode;
 }

以上就是图遍历的简单应用了，很简单，多练几道题就能轻松掌握。