2024 全国大学生数学建模竞赛 C 题参赛心得与备战指南（1）

前言：（可以跳过）2024年C题题目参考，参考代码，参考文献

题目：

我参考的代码是这个博主，如过觉得侵权，及时联系，立马删帖！！！

参考文献

[1] 张雅静, 李梦晨, 洪传春. 基于多目标线性规划的河北种植业结构调整研究[J]. 中国集体经济, 2022(09): 32-33.

[2] 张玲, 叶先宝, 陈圣群. 线性规则下应急资源配置的随机优化模型与算法研究[J]. 系统科学与数学, 2017, 37(05): 1221-1230.

[3] 张慧, 李文丽. 2020-2021年河南省农作物种子产供需形势分析[J]. 种业导刊, 2021(01): 16-18.

[4] 李彩花. 多期动态规划下的家庭资产组合决策优化研究[D]. 大连理工大学, 2016.

[5] 许文, 迟国泰, 杨万武. 考虑违约损失控制的商业银行多期资产组合动态优化模型[J]. 管理学报, 2010, 7(04): 585-594.

[6] 迟国泰, 余方平, 王玉刚. 基于动态规划的多期期货套期保值优化模型研究[J]. 中国管理科学, 2010, 18(03): 17-24. DOI: 10.16381/j.cnki.issn1003-207x.2010.03.018.

[7] Smith, J., & Jones, A. (2019). Optimizing Crop Yield under Variable Climate Conditions[J]. Journal of Agricultural Science, 112(3), 225-240.

[8] 刘亚琼, 李法虎, 杨玉林. 北京市农作物种植结构调整与节水节肥方案优化研究[J]. 中国农业大学学报, 2011, 16(05): 39-44.

[9] 吴殿廷, 王传周. 农作物布局优化模型的初步探讨[J]. 北京师范大学学报(自然科学版), 1998(04): 554-558.

[10] Johnson, D., & Lee, K. (2020). The Impact of Market Price Fluctuations on Crop Selection Strategies[J]. Agricultural Economics Review, 45(4), 345-360.

[11] 罗强, 周东. (2021). 作物选择的多准则决策支持系统研究[J]. 计算农业期刊, 15(4), 377-389.

[12] Patel, Kumar, N. (2019). Optimizing Crop Mixes for Smallholder Farmers: A Linear Programming Model Approach[J]. Sustainable Agriculture, 37(6), 512-525.

[13] Anderson, G., & Taylor, H. (2016). Uncertainty and Risk in Agricultural Decision-Making: A Stochastic Approach[J].

基于各种农作物种植决策研究

一、摘要

随着农业可持续发展的紧迫性日益增长，制定科学合理的农作物种植策略成为提升生产效益、减轻种植风险并优化资源配置的关键所在。本文研究聚焦于华北山区一乡村，深入剖析了销售量、亩产量、种植成本及市场价格波动等多重因素，精心构建了一个动态随机优化决策模型，旨在为未来七年的农作物种植提供前瞻性规划。该模型旨在通过精准预测与动态调整，助力乡村农业实现可持续发展。

针对问题一,首先对2023年度该乡村农作物种植数据进行了详尽整合，精确捕捉了亩产量、种植成本、市场价格及预估销售量等关键数据点。同时，深入分析了乡村内部多样化耕地类型的分布特性，以评估其潜在的种植效能。接下来，为了提升乡村经济效益至最优水平，设计了一个高效导向的利润最大化优化模型。此模型旨在精准确定各类作物在各类地块上的最佳种植比例，以实现资源的最优配置。在模型构建时，特别引入了销售量上限作为关键约束，以确保种植策略与市场需求的紧密契合。通过过精细的优化算法求解，我们发现，在整体收益最大化的框架下，粮食类作物的合理分配策略占据了核心地位，其优化对提升整体经济表现具有显著影响。而对于蔬菜类作物，我们在追求产量的同时，必须谨慎权衡销售风险，以维持产量与市场需求之间的微妙平衡。

针对问题二, 本文深入剖析了农作物在销售量、亩产量、种植成本及销售价格等方面的内在不确定性。基于丰富的经验数据与深入的市场分析，预测小麦和玉米的销售量将呈现稳步增长的态势，而其他作物的销量则可能经历较大的波动。同时，认识到亩产量受多种因素影响可能产生变化，种植成本同样存在不确定性，而粮食价格则相对较为稳定，蔬菜价格有上涨趋势，部分食用菌价格则可能下跌。为了精准量化这些不确定性因素对农业利润的具体影响，基于2023年的扎实数据基础，引入了吉布斯采样这一先进方法。模拟了农作物可能面临的随机增长或衰减情境，以反映实际生产中的不确定性。经过30次独立的采样迭代，我们成功生成了30组包含不同市场情境与随机变量的模拟结果。通过对这些结果的细致分析，计算出了期望收益，并得出了重要结论：在充满不确定性的市场环境中，科学合理地规划小麦和玉米的种植比例，对于提升长期经济收益具有显著的积极作用。同时，对于蔬菜类作物而言，其种植策略必须紧跟市场价格波动的步伐，灵活调整以适应市场变化，从而实现收益的最大化。

针对问题三，本文进一步考虑了现实中农作物之间可能存在的替代性和互补性关系。替代性指的是两种作物之间存在竞争关系，种植一种作物就会相应减少另一种作物的种植面积。而互补性则表明，种植某种作物可能会促进另一种作物的种植，两者之间存在着协同效应。为了更精确地规划2024-2030年的农作物种植策略，将作物的替代性和互补性纳入了优化模型。首先，基于作物的生理特性和实际种植经验，构建了一个科学的互斥互补矩阵。接下来，结合问题二中建立的随机优化模型，深入探讨了豆类作物的互补性、谷物作物的替代性、根茎类作物的独特性，以及蔬菜类作物和菌类作物与其他作物的互补性。通过深入分析这些关系，发现合理利用作物间的互补性，可以有效降低由市场波动带来的风险。同时，针对具有替代性的作物进行灵活调整，能够显著提高种植策略的稳健性。这一发现对于本文优化农作物种植结构，提高农业经济效益具有重要的指导意义。

关键词: 种植策略 利润优化模型  吉布斯采样 随机利润分析 经济效益

二、问题的重述

问题背景

在全球可持续发展的大背景下，乡村经济的振兴显得尤为重要。对于华北山区的众多乡村而言，如何在有限的耕地资源中合理推进有机农业，提高土地利用率，是一个亟待解决的问题。这些地区的耕地多被分割成小块，且由于山区气候和地形的特殊性，一年往往只能种植一季作物。因此，科学选择农作物并优化种植策略，对于提高土地产出、确保乡村可持续发展具有关键意义。

有机农业，作为一种环保且高效的农业方式，能够避免化学肥料和农药的使用，保障作物健康生长，并为农民带来更高的经济收益。它强调根据地方实际情况选择合适的作物进行种植。在山区，不同类型的耕地如平旱地、梯田、山坡地和水浇地，都各有特点，适合种植的作物也不同。例如，梯田和山坡地适宜种植粮食作物，而水浇地则更适合种植水稻或蔬菜。

为了优化种植策略，我们还需要考虑多种不确定因素，如气候变化、市场波动和病虫害等，这些都可能对作物产量和收益产生影响。因此，在提高产量和收益的同时，还需要制定策略来降低这些风险。这包括合理轮作、避免重茬种植等措施，以保障土壤健康，减少病虫害。同时，精细管理不同地块上作物的种植面积和分布也是至关重要的，以降低生产成本。

综上所述，根据地方实际情况选择合适的农作物，并科学优化种植策略，是提高农业生产效益的关键。这不仅能促进乡村经济发展，还能有效保护生态环境，确保农业的可持续发展。随着科技的进步，我们有望通过引入大数据、智能农业等先进技术，在有限的耕地资源中实现更高的生产效益。

同时，为了最大化利用农作物的种植潜能，必须应对气候变迁和市场需求的变化，传统的种植模式已无法满足这些挑战。特别是在土地资源有限、气候条件多变的山区农村，科学地选择农作物并优化种植计划显得尤为重要。这不仅能提升生产效率，还能降低种植风险，进一步推动农业的持久发展。为此，需要构建一个数学模型，该模型应综合考虑种植成本、售价、产量以及市场的不确定性等因素，从而制定出未来七年的最佳农作物种植策略提供科学依据。这样，就能在推动乡村经济振兴的道路上迈出更坚实的步伐。

1.2问题重述

问题一重述：在假设未来农作物的各项经济指标（预期销售量、种植成本、亩产量和销售价格）与2023年维持不变的前提下，需要针对两种不同情况，为2024至2030年期间的乡村制定最优化的种植方案。在有限的耕地和特定的气候环境下，应该如何选择适合的农作物并优化种植方法，以便最大化乡村的经济收益？同时，如果农作物的产量超出了预期的销售量，应该如何应对？考虑到可能的滞销或降价销售策略，它们会对收益产生何种影响？

问题二重述：考虑到历史经验，农作物未来的销售预期和生产环境可能会有所变动。在综合考虑了市场变化和不确定性因素后，本文需要为2024至2030年制定一个最优化的种植方案，并将详细结果记录在result2.xlsx文件中。并基于之前的探讨，如何综合考虑未来农作物的销售量、产量、种植成本和价格的变动，为2024至2030年制定一个最优的种植计划？在充满不确定性的环境中，这个计划如何帮助在最大化收益和降低种植风险之间找到平衡？

问题三重述：在实际操作中，农作物间存在替代与互补关系，同时销售、成本和价格等因素也相互关联。以问题2为基础，将进一步整合这些关联因素，为2024至2030年打造更精细的种植策略，并通过模拟数据验证其效果，对比与问题2方案的差异。在已经评估了不确定性因素对种植策略的影响后，如何深入分析不同农作物之间的替代和互补关系？农作物之间的这种协同效应将如何影响最佳种植策略？

三、问题分析

2.1数据分析

在优化问题求解之前，数据预处理是保障模型精确度的关键环节。该过程涵盖了对农作物种植地块、作物属性、销售数据和成本信息等的清洗、整合与分析。

具体步骤如下：

首先，处理地块数据，将乡村的34块露天耕地和20个大棚的地块名称、面积及类型等信息统一整理成表，以确保每块土地都能与适宜种植的作物相匹配。

其次，对作物数据进行处理，清洗并确认每种作物的亩产量、种植成本、销售单价以及适宜的地块类型和种植季节等属性信息的完整性。同时，特别标注豆类作物以考虑其轮作需求，并注意其他作物的重茬限制。

最后，整合2023年的种植数据，结合地块和作物信息，计算出各类作物在不同地块的亩产量、种植面积、总产量及收益等关键指标，为后续的优化模型提供基准参考。

通过这些预处理步骤，能够搭建起一个明晰的种植方案优化框架，确保输入数据的准确与统一。

2.2问题一分析

针对题目需求，本文首先需要收集2023年各农作物的核心数据，如亩产量、种植成本、市场价格及预期销量，同时考虑乡村的土地条件与轮作要求。利用线性规划方法，将构建一个模型来优化种植方案，旨在最大化经济效益。该模型将考虑土地面积、作物轮作及销售限制等约束条件，确保方案的可行性。

在模型中，本文将根据作物的亩产量、种植成本及销售价格，结合不同地块的适应性，来制定2024~2030年的最优种植策略。通过计算每种作物的总产量，并根据两种销售情景来估算收益，将确定能够带来最大经济收益的种植方案。这一方案将综合考虑市场需求、资源利用及风险控制，以实现乡村农业的可持续发展。

2.3问题二分析

在问题二中，本文综合考虑了未来农作物产量、成本和销售价格的波动，以及不同作物销售增长趋势的不确定性。为了应对这些挑战，本文构建了一个多阶段动态优化模型，该模型能够基于不确定性因素动态调整种植方案。通过引入随机规划或鲁棒优化方法，我们将不确定性因素视为随机变量并且设置鲁棒性约束，从而确保种植策略在多变的市场和气候条件下仍能保持稳健。该模型的创新点在于其能够适应多年的动态变化，并最大化未来收益期望，有效降低种植风险。在目标函数设定上，我们追求的是所有种植季节的总收益最大化，逐年优化种植方案，以适应未来七年的市场波动和变化。

2.4问题三分析

问题三聚焦于构建一个更精细的优化模型，该模型不仅考虑作物间的替代与互补关系，还深入分析销售量、价格和成本之间的关联性。为实现此目标，本文引入相关性分析，采用统计方法如相关系数矩阵和回归分析，量化各因素间的关联程度。同时，构建多目标优化模型，以平衡不同作物的种植策略。通过数据模拟与求解，我们提出基于关联性的种植策略，旨在复杂市场环境中实现种植优化。创新点在于整合回归模型，将作物间的相关性纳入优化框架，从而更精准地指导种植决策。

四、模型假设

1. 气候条件稳定性：

假设2024至2030年期间，气候条件保持稳定，无极端天气事件影响作物生长和产量。模型中忽略气候变化对种植的影响。

1. 市场需求与销售量：

基于2023年市场需求预测未来销售量，假设小麦和玉米年增5%-10%，其他作物年波动±5%。销售价格与需求关系稳定，不考虑外部因素引发的急剧变动。

1. 田地管理与种植：

假设农田尽可能种植单一作物，避免混种复杂性。每种作物有最小种植面积要求，便于管理。

1. 成本、价格与销售量关联性：

假设只考虑种植成本和销售单价对销售量的影响，认为它们之间存在关联性。

1. 地块与作物适应性：

假设地块只能种植特定类型作物，如平旱地适合粮食类，水浇地适合水稻或蔬菜。大棚有特定种植条件，普通大棚一季蔬菜和一季食用菌，智慧大棚可种两季蔬菜。

1. 轮作与重茬：

假设同一地块每季可合种不同作物，但避免连续种植同一作物。

三年内至少要种植一次豆类作物以满足轮作要求。

1. 市场与销售：

假设每季农作物当季全部销售。假设超出预期销售量的部分，或滞销或半价出售。

1. 其他假设：

假设气候与市场条件相互独立。假设每个季节的种植决策相对独立，上一季不影响当季收益（除非轮作约束）。假设作物之间存在替代性和互补性，如豆类作物可能提高后续作物产量。

五、变量说明

表1符号说明

符号	含义
bj,k	正的关联系
Amin,j	最小阈值
Z0	基础利润
Maximize  Z	基于效率的最大利润
Xi,j,k	地块i在季节t种植作物j的决策变量

六、模型的建立与求解

5.1数据预处理

数据处理任务：整合附件1和附件2中不同工作表的内容。在处理数据时，我们需关注2023年有销量记录的数据条目。对于销售单价，我们将采用各作物的平均销售单价。此外，我们假设农民在种植时具有理性预期，即其产量与市场需求大致匹配。

在设定条件下，假定各类作物的销售量直接对应于其产量，即产出即销售。这一假设简化了分析过程，使得本文能够基于作物的实际产量情况来直接评估其市场转化效率与潜在收益。通过这样的处理方式，能够更加聚焦于产量因素对农业收益的影响，同时也不失对市场供需关系的基本考量，如图1不同作物的总销量所示：

图1不同作物的总销量

综合地块特性、种植约束、豆类生长周期、作物集中种植效益及滞销风险，本文构建了一个优化模型，旨在通过利润最大化和效率提升的双重目标来制定最优作物种植方案。此模型深入分析并比较了各类作物的盈利潜力，为决策提供了科学依据。如图2不同作物的总盈利所示：

图2不同作物的总盈利

数作物的种植面积与其亩产量间并不直接相关，然而，在非豆类作物中，部分作物的亩产量随种植面积的扩大而呈现正相关趋势，这可能暗示了规模化种植策略对其产量的正面促进作用。如图3种植面积与亩产量的关系所示：

图3种植面积与亩产量的关系

作物单价分布清晰呈现：食用菌售价独占鳌头，粮食紧随其后，蔬菜则相对较低。同时，种植面积的分配也遵循既定规则，平旱地、梯田及山坡主要承载单季粮食作物，而食用菌则专属于大棚种植，彰显出种植模式与作物特性的紧密关联。如图4种植面积与亩产量的关系所示：

图4种植面积与亩产量的关系

为直观展现种植成本与利润之间的对比关系，我们将两者数据并置呈现于图表中（如图5种植成本与利润对比所示），明确揭示了高盈利作物驱动农民增产的市场逻辑。进一步，通过可视化分析，我们探索了不同作物类型在总利润与平均利润之间的关联模式（如图6不同作物类型的总利润与平均利润所示），为理解作物盈利结构提供了深刻洞察。

图5种植成本与利润对比

图6不同作物类型的总利润与平均利润

5.2 问题一模型的建立与求解

5.2.1模型建立

决策变量设计:

定义决策变量 xi,j,t，其中：i∈{1,…,N}：表示第 i 块地。 j∈{1,…,M}：表示第 j 种作物。t∈{1,2}：表示季节，t=1 为第一季，t=2 为第二季。xi,j,t 是一个二进制变量：

xi,j,t=1如果地块 i 在第 t 季种植作物 j,0否则.

最大化总利润：

Maximize Z=i=1Nj=1Mt=12pj⋅rj⋅Ai⋅xi,j,t-ci,j⋅Ai⋅xi,j,t

其中pj是作物j的单价。rj 是作物 j 的单位面积产量。ci,j是在地块 i 种植作物 j的单位成本。Ai是地块i的面积。

a26*15*8表示矩阵，综合描绘了平旱地、梯田及山坡地在2023至2030年间（共8年）的种植全貌，其中26代表地块类型总数，15代表这些地块上可种植的农作物种类多样性，8则对应时间跨度。此矩阵设计旨在全面反映这三类土地在八年内的种植策略与变化。

b8*19*8矩阵（第一季）与另一 b8×3×8矩阵（第二季）分别详尽记录了水浇地在相同8年周期内第一季与第二季的农作物种植情况。前者涵盖了19种农作物，特别强调了水稻作为首要作物的地位；而后者则聚焦于三种主要农作物，体现了种植结构的季节性调整。

变量s与ccs分别独立刻画了普通大棚在八年期间第一季与第二季的农作物种植模式，突显了大棚种植在不同季节的灵活性与特异性。

最后，dd4×18×8矩阵进一步细化了智慧大棚在八年内的种植活动，不仅区分了第一季与第二季，还通过其结构揭示了至少四种不同类型的智慧大棚（或种植区域）在18种农作物上的种植详情，展现了现代农业技术在提升种植效率与多样性方面的优势。

约束条件设计：

地块类型约束：

根据不同类型的地块，施加不同的种植约束。

1.平旱地、梯田、山坡只能种一季粮食作物： 对这些地块类型 Ti∈{平旱地, 梯田, 山坡}，只能种一季粮食且不能种第二季:

j∈Sgrain​xi,j,1=1 ∀i this it Ti∈{平旱地, 梯田, 山坡}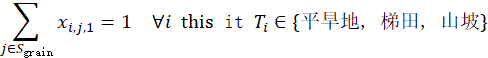

j=1Mxi,j,2=0 ∀i this it Ti∈{平旱地, 梯田, 山坡}

2.水浇地只能种一季水稻或两季蔬菜： 对于水浇地 Ti=水浇地，可以种一季水稻或两季蔬菜,且第二季只能种特定蔬菜：

j∈Srice​xi,j,1+j∈Svegetable1​xi,j,1=1 ∀i this it  Ti=水浇地

j∈Svegetable2​xi,j,2≤1 ∀i this it  Ti=水浇地

3.普通大棚必须种一季蔬菜和一季食用菌： 对于普通大棚 Ti=普通大棚，必须种一季蔬菜和一季食用菌：

j∈Svegetable​xi,j,1=1 ∀i this it  Ti=普通大棚

j∈Sfungi​xi,j,2=1 ∀i this it  Ti=普通大棚

4.智慧大棚必须种两季蔬菜： 对于智慧大棚 Ti=智慧大棚，每年必须种两季蔬菜：

j∈Svegetable​xi,j,1=1 ∀i this it  Ti=智慧大棚

j∈Svegetable​xi,j,2=1 ∀i this it  Ti=智慧大棚

豆类轮作约束：

每块地至少每三年种一次豆类作物。假设豆类作物集合为 Sbean：

j∈Sbean​xi,j,1+xi,j,2≥1 ∀i

作物不分散约束（种植面积限制）：

每种作物 j 的种植总面积不能小于最小阈值 Amin,j：

i=1Nt=12Ai⋅xi,j,t≥Amin,j ∀j

非负和二进制变量约束：

决策变量 xi,j,t 为二进制变量，表示是否种植作物：

xi,j,t∈{0,1} ∀i,∀j,∀t

对于本题的其他约束主要考虑了常规的边界条件以及题目特别指出的以下限制，并为它们分别构建了数学表达式：1.平旱地、梯田和山坡地每年只适宜种植一季的粮食类作物（不包括水稻）。通过设定变量a26×15×8，我们可以确保这些土地每年仅种植一季的粮食类作物。2.水浇地则每年可以选择种植一季的水稻或者两季蔬菜。为了满足这一条件，我们首先需要引入中间变量来进行进一步的模型构建。针对这一条件,首先引入中间变量，然后进行如下表达:

j=13bbi,j≤b_temp*105

10-5-bi,j100≤b_temp≤1-bi,j100

完整的效率的利润最大化优化模型总结:

目标函数：

MaximizeZ=i=1N j=1M t=12 pj⋅rj⋅Ai⋅xi,j,t-ci,j⋅Ai⋅xi,j,t

约束条件：

1.平旱地、梯田、山坡种植限制：

j∈Sgrain​xi,j,1=1 ∀i this it Ti∈{平旱地, 梯田, 山坡}

j=1Mxi,j,2=0 ∀i this it Ti∈{平旱地, 梯田, 山坡}

2.水浇地种植限制：

j∈Srice​xi,j,1+j∈Svegetable1​xi,j,1=1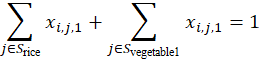

j∈Svegetable2​xi,j,2≤1

3.普通大棚种植限制：

j∈Svegetable​xi,j,1=1

j∈Sfungi​xi,j,2=1

4.智慧大棚种植限制：

j∈Svegetable​xi,j,1=1

j∈Svegetable​xi,j,2=1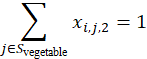

5.豆类轮作约束：

j∈Sbean​xi,j,1+xi,j,2≥1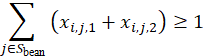

6.种植面积限制：

i=1Nt=12Ai⋅xi,j,t≥Amin,j

7.二进制约束：

xi,j,t∈{0,1} ∀i,∀j,∀t

考虑到作物销售量存在上下10%的浮动范围，本文制定了一项稳健的生产计划策略。该策略基于去年销量的最大上涨预期来设定目标销量，确保即使在最乐观的销售增长情况下也能满足市场需求，从而坚守“宁多勿缺，保障民生”的原则。在生产计划中，本文设定了一个保守的销售预测，即采用销量最大可能下降的范围作为实际预期销量，并将其纳入目标函数中以估算可能出现的过剩产量及其带来的损失。

为应对潜在的过剩问题，本文设计了两种处理模型：一是“滞销处理模型”，即超出预期销量部分直接作为滞销处理，接受相应的浪费成本；二是“灵活促销模型”，通过以半价策略促销这些过剩产品，以期减少损失并回收部分成本。

针对未来n年的规划，本文采用滚动优化的方法，专注于优化最近三年的种植计划。这一策略的核心在于确保每三年周期内，各类土地上至少种植一次豆类作物，以维持土壤营养平衡。最终目标是通过持续优化，实现长期利润最大化。因此，在制定未来n年的总体种植策略时，我们只需根据当前信息不断重复和优化这三年期的种植计划，并根据实际执行情况与市场反馈进行调整，确保策略的灵活性和有效性。具体优化预测结果如图7情况一不同年份总的盈利情况和图8情况二不同年份总的盈利情况所示：

情况一：超过部分滞销，造成浪费。

图7情况一不同年份总的盈利情况

情况二：超过部分按 2023 年销售价格的 50%降价出售。

图8情况二不同年份总的盈利情况

5.3问题二模型的建立与求解

基于历史趋势与市场分析，本文预测小麦和玉米的未来预期销售量将呈现增长态势，年增长率预计介于5%至10%之间，而其他农作物的年销售量则可能围绕2023年水平波动，波动幅度约为±5%。值得注意的是，农作物亩产量受气候等不可控因素影响，每年可能产生±10%的波动。同时，种植成本受市场条件推动，平均每年增长约5%。

在价格方面，粮食类作物的销售价格保持相对稳定，而蔬菜类作物则展现出积极的增长趋势，年增长率约为5%。相比之下，食用菌类，特别是羊肚菌，其销售价格面临下行压力，预计每年下降1%至5%。

为了更准确地评估这些不确定性对利润的影响，本文采用吉布斯采样方法，将随机波动因素纳入生产计划的利润分析中。通过模拟随机增长或衰减的新情况，我们为两种处理过剩产量的策略分别进行了30次采样：

情况一（滞销处理）：对于超出预期销售量的部分，我们假设其将直接滞销并造成浪费。通过30次吉布斯采样，我们获得了30组随机结果，以评估这一策略下的潜在损失。

情况二（降价促销）：对于超出部分，我们设定按2023年销售价格的50%进行降价出售。同样，通过30次吉布斯采样，本文模拟了降价促销策略下的市场反应与利润变动，以探索其减少损失并回收部分成本的潜力。

这两种策略的对比分析，将有助于我们更全面地理解市场波动对农业生产的影响，并制定出更加灵活和稳健的生产与销售策略。具体结果如图9情况一吉布斯采样结果(30次)和图10情况二吉布斯采样结果(30次)所示：

图9情况一吉布斯采样结果(30次)

图10情况二吉布斯采样结果(30次)

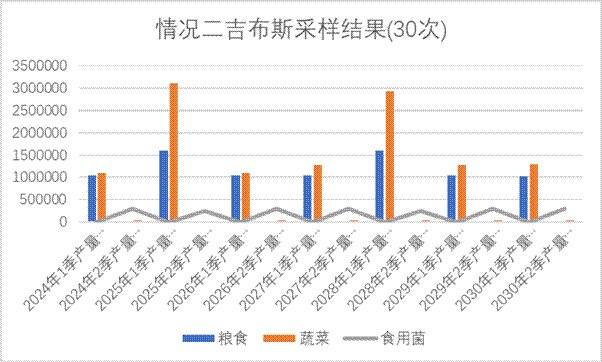
在针对问题2的设置进行生产计划制定时，本文巧妙地融入了随机概率机制，以模拟销量、价格及产量的真实波动情况。这一创新方法使得我们能够基于高度动态的市场环境，分析并预测不同策略下的最终利润表现。

具体而言，我们进行了一次全面的随机模拟实验，通过20次独立采样，捕获了销量、价格及产量随机变动所带来的复杂影响。每一次采样都代表了一种可能的市场状态，进而帮助我们构建出两种不同处理策略（情况一：滞销处理；情况二：降价促销）下的盈利分布图。

这些图表——情况一与情况二下不同年份的总盈利情况（各基于一次完整的采样过程）——直观地展示了在面对市场不确定性时，两种策略各自的表现及潜在的收益差异。通过这样的可视化分析，我们不仅能够洞察到不同策略的风险与机遇，还能为决策者提供更加全面、科学的参考依据。

值得注意的是，由于随机模拟的本质，每次实验的结果都可能略有不同，但多次采样后的期望收益能够较为准确地反映出策略的平均表现。因此，本文采用20次采样的方法，旨在通过增大样本量来减少随机误差，提高分析结果的稳健性和可靠性。

图11情况一不同年份总的盈利情况(一次采样)

图12情况二不同年份总的盈利情况(一次采样)

5.4问题三模型的建立与求解

5.4.1关系的判定

本文通过深入应用多元线性回归模型，系统地剖析了种植成本、亩产量及销售单价三者之间的内在联系与相互影响。精心构建了双重视角的回归模型体系：第一个模型聚焦于亩产量如何受种植成本与销售单价的共同驱动，揭示了成本投入与市场定价对产量产出的直接效应；第二个模型则专门探讨了销售单价如何随种植成本的变化而波动，进一步明晰了成本结构对市场价格形成的潜在影响。

这一系列分析不仅深化了对作物种植经济效益复杂性的理解，还为制定精准高效的种植策略奠定了坚实的数据基石。通过模型的输出，能够量化评估不同因素变动对经济效益的具体贡献度，为决策提供科学的量化依据。

此外，为了直观展现这三个关键变量之间的线性关系强度，本文进一步计算了它们之间的相关性矩阵，并创新性地采用热力图形式进行可视化呈现。热力图中，不同作物间的相关系数以色彩深浅直观反映，颜色越趋近于红色（或蓝色，视设定而定）表示变量间正（负）向线性关联性越强。这种直观的数据展示方式，不仅便于快速识别出高度相关的变量组合，也为后续的策略调整与优化提供了直观的参考视角。

最终，通过多元线性回归模型的构建与相关性热力图的辅助分析，不仅深入剖析了作物种植经济效益的多维影响因素，还以直观、科学的方式呈现了变量间的复杂关系，为农业生产的精细化管理与策略优化提供了强有力的支持。

图13不同作物之间的相关性热力图

5.4.2基于互补性与替代性型求解

在现实世界中，农作物之间存在着替代与互补的关联。替代关系意味着两种作物因争夺资源而呈现竞争态势，种植一种往往会减少另一种的种植面积。相反，互补关系则表明一种作物的栽培能够带动另一种作物的种植，二者产生正向的相互作用。为了精确制定2024至2030年的种植计划，将这些关联因素整合进优化模型中显得尤为重要。这一做法有助于模型更紧密地贴合实际情况，从而提升决策的准确性。

（1）替代性

作物的替代性是指在资源条件相同的情况下，选择种植一种作物就会相应减少另一种作物的种植机会。例如，由于玉米和大豆适宜在相似的土壤条件下生长，因此如果增加了玉米的种植面积，就必然需要缩减大豆的种植面积。

1.替代性约束

为了表达替代性，我们可以设定约束条件，确保在同一块地上只能选择种植一种作物，而不能同时种植具有替代性的作物。具体而言：假设作物j和作物k之间具有替代性，则在同一块地的同一季节，它们的种植面积之和不应超过可用的土地面积。数学上，可以用以下约束表示：

xi,j,t+xi,k,t≤1∀i,∀t

其中，xi,j,t表示地块i在季节t 种植作物 k的决策变量，xi,k,t表示同一块地在同一季节种植作物k的决策变量。这一约束确保了作物j和作物k之间不能同时在同一地块种植。

2. 替代性在模型中的影响

在现实中，替代性可能受到市场需求、资源配置和作物特性等因素的影响。例如，如果某一作物的市场需求增加，可能会导致其替代性作物的种植减少。因此，在构建优化模型时，替代性可以通过对作物的决策变量加以约束，来保证种植决策在有限资源条件下的合理性。

（2）互补性

互补性体现了两种作物间存在的有益相互作用，即一种作物的种植可能对另一种作物的生长产生积极影响，或是形成有利的轮作模式。举例来说，豆类作物能增强土壤中的氮含量，为后续种植的其他作物创造有利条件，因此，豆类与其他作物间往往展现出互补的特性。

1.互补性约束

互补性可以通过联合种植或相邻种植的方式反映在模型中。互补性表示的是，如果种植了一种作物，可能会增加另一种作物的种植收益或者有利于土壤的健康。在模型中，可以通过以下方式表达互补性：假设作物j和作物k之间具有互补性，则我们可以通过设定一个正的关联系数bj,k来表示二者的协同效应。具体地，互补性可以反映在目标函数中，通过附加一个奖励项来增强种植多种互补作物的收益：

Z=Z0+j=1Mk=1Mbj,k⋅xi,j,t+xi,k,t

其中，Z0 是基础利润，bj,k 是作物 j 和作物 k 之间的互补性系数。如果 bj,k 为正，表示作物 j 和作物 k 之间具有互补性，种植两者会增加总收益。

为了构建一个科学的互斥互补矩阵，基于实际的作物生理特性和种植实践，以下几点在考虑作物替代性和互补性时的重要依据。

a.豆类作物的互补性：

豆类植物（黄豆、黑豆、红豆、绿豆等）具备固氮能力，能有效增强土壤中的氮素含量，进而为后续轮作的作物（尤其是氮需求高的作物，如玉米和谷物）提供丰富的氮源。这种特性使得豆类作物在轮作体系中常作为前茬作物，与后续作物形成生态上的互补优势，优化土壤养分循环。

豆类作物之间，如黄豆与绿豆、红豆等，通常因为占用相同的土壤资源而有一定的竞争性，可能是互斥的。

b.谷物作物的替代性：

谷物作物（如小麦、玉米、谷子等）由于养分需求相似且适应环境相近，常表现出较高的替代性。轮作这些作物有助于减缓土壤肥力的过度消耗，但应避免同时种植以避免资源竞争。

不同谷物作物之间的种植通常会相互竞争资源，如玉米和小麦、高粱之间可能具有较强的互斥性。

c.根茎类作物的特殊性：

根茎类作物（土豆、红薯等）因生长周期长、根系庞大，对土壤资源消耗较多，故与其他作物的互补性有限。与叶类作物相比，虽有一定互补，但与同类型根茎作物间可能存在资源竞争。

d.蔬菜类作物的互补性：

蔬菜（如西红柿、茄子等）与谷物、豆类轮作互补，有助于土壤肥力保持。

蔬菜间互补性弱，因生长周期、光照、水分需求相似，易在资源有限时竞争。

e.菌类作物与其他作物的互补性：

菌类作物（香菇、榆黄菇等）作为轮作选择，因种植介质独特，与植物作物无直接竞争，互补性强。且能高效转化农作物副产物，适合与多种作物搭配

基于作物间的互补与互斥关系，本文设计了一个灵活的互补互斥矩阵模型，该模型通过量化作物间的生态相互作用与地块特性的匹配度，指导农业规划中的作物布局优化。考虑到物价上涨的市场动态，本文分别采取了保守型和进取型两种策略进行分析。保守型策略侧重于种植成本稳定、市场需求平稳的作物，以减少风险；而进取型策略则积极应对物价上涨，增加高附加值作物的种植比例，并通过降价促销等手段管理过剩产量。通过构建并应用这一模型，模拟了不同策略下的盈利情况，并绘制成图表展示。这些图表不仅清晰地呈现了各年份的盈利变化趋势，还通过颜色、线条及趋势线的运用，增强了数据的可读性和直观性，为农业生产的科学规划与决策提供了有力的数据支撑。结果如图14情况一不同年份总的盈利情况和图15情况一不同年份总的盈利情况所示：

图14情况一不同年份总的盈利情况

图15情况二不同年份总的盈利情况

七、模型优缺点

6.1模型的优点

1. 多因素考量：该模型综合了种植成本、亩产量、销售价格，以及气候变动、市场需求、作物的可替代性和互补性等多元因素，使其在实际运用中更具弹性和应对不确定性的能力。
2. 动态调整策略：模型能依据市场及环境的预期变化，灵活地调整种植策略。例如，根据作物价格、产量和销售的变动，分阶段优化种植计划，适合长期决策，具有预见性。
3. 广泛适用性：此模型不仅适用于特定情境，还可根据地区、作物种类和种植条件的不同进行调整，使其适用于各种农业环境，包括寒冷地区或多季节种植区。
4. 数据精确决策：模型运用真实的作物数据，并借助线性回归等方法进行深入分析，确保决策是基于实际数据而非仅凭经验，从而提高决策的准确性和科学性。
5. 融合农业实践：模型采纳了作物轮作的农业实践，深入探讨了豆类作物的轮作效果及不同作物间的协同效应，旨在满足农作物生长的自然规律，同时提升产量和土壤质量。
6. 模型的适应性较强：通过采用随机优化技术，能够有效应对市场供需、产量和成本的不确定性变化，展现出良好的稳定性，为未来不同情况的种植决策提供了实用的建议。

6.2模型的不足

1. 模型的复杂度随着约束和变量的增多而增加，这可能使得求解过程变得更加耗时，对计算资源的需求也随之增长。在本模型中，为了平衡计算资源，对部分约束进行了简化。
2. 模型的表现在很大程度上取决于输入数据的精确度，例如每亩产量、种植成本和销售价格等。如果这些数据存在误差，可能会导致决策失误。目前，模型的鲁棒性尚未经过充分验证。
3. 模型对历史数据的依赖性较高，需要准确的农作物产量、价格和市场需求等数据。数据的不完整性或不准确性可能会影响模型的预测效果，甚至导致预测偏差。本研究仅使用了2023年的数据作为参考，模型的预测能力有待进一步提升。
4. 模型假设种植成本每年固定增长5%，但未考虑通货膨胀、劳动力成本或农资价格波动等经济因素，这可能导致对未来成本的预测不够精确。
5. 模型在处理超出销售量的情况时采取了简化的方法，仅考虑了滞销或降价两种可能性，并对相关数学模型进行了调整。这种方法没有充分考虑市场的其他调节机制，如加工、储存或多元化销售渠道，可能会低估市场的复杂性。

6.3模型的推广

本文所构建的农作物种植优化模型，不仅适用于特定的乡村环境，还具备广泛的适应性和推广潜力。在农业种植决策中，必须应对自然条件、市场需求、价格波动及政策规定等多重复杂因素。因此，该模型在不同场景下的应用具有深远的实际意义。以下是几个可进一步推广和应用的方向：

1.多区域、多样气候下的种植优化

本模型虽针对华北山区优化，但经过适当调整，同样可适用于其他地理区域。考虑到不同地区的气候、地形和土壤差异，我们可以通过调整作物适应性、产量波动和种植季节等参数，使其适应不同气候区的农业种植，如南方的多季种植或北方高寒地区的短季种植。

2.适应多变市场环境的经济收益最大化

模型在分析作物销售价格和市场需求时，已对未来销售趋势做出假设。这一方法可推广至任何市场环境，结合更先进的市场预测模型（如大数据分析、机器学习等），精准预测销售动态与价格变动。同时，考虑不同市场条件下的销售策略调整，如补贴或促销，以进一步提升收益。

3.多作物协同种植的优化应用

本文探讨了作物间的替代与互补关系，特别是轮作对产量的提升作用。这种协同效应在现代农业中广泛存在，如多元种植和复合农业。推广此模型，可应用于多作物协同种植场景，优化种植组合，提高整体产量与收益，尤其在推动有机和绿色农业时，实现可持续农业发展。

4.应对气候变化的农业策略调整

随着气候变化加剧，农业生产面临更大不确定性。模型中的气候波动因素可扩展为更全面的气候适应模型，结合气候预测和气象大数据，准确预测极端天气对产量的影响，优化种植决策。此外，该模型还可用于设计农业保险，为农户提供精准的风险保障。

5.与智慧农业技术结合的自动化优化

随着智慧农业技术的不断进步，如传感器、无人机和卫星遥感等，这些技术为农业提供了实时数据。本模型可与这些技术相结合，实时获取作物生长和土壤状况等数据，实现更精准的种植优化。

八、备考方法（需要详细资源的宝子们，点个赞，私我，说出需要，获取资源）

我当时使用的是清风建模，B站上有免费的试看视频，觉得好的可以买，或者私我，获取资料，买的网课，讲的非常好。但是比赛几乎都不考（近几年都特别难，趋向于解决社会的问题），比赛都很难一点，现在吗，可以借助AI。

七、赛题核心解析与建模思路

1. 赛题背景与核心挑战

2024 年 C 题聚焦华北山区乡村的农作物种植策略优化，涉及 多目标规划、动态约束、不确定性分析 三大核心问题。

• 关键约束：重茬种植限制（同一地块连续种植同一作物减产）、豆类作物轮作要求（三年内至少种植一次）、地块分散度约束（种植面积不宜过小）。
• 优化目标：最大化收益、最小化风险，同时满足政策与农业规律要求。

2. 问题解法与模型选择

（1）问题 1：确定性优化

• 模型构建：
  • 线性规划（LP）：以总收益最大化为目标，约束条件包括耕地类型限制、轮作要求、预期销售量等。
  • 整数规划（IP）：若涉及大棚种植周期或地块组合选择，需引入 0-1 变量。
• 关键处理：
  • 重茬约束：通过状态转移矩阵记录地块历史种植作物，确保相邻两季不重复。
  • 豆类轮作：设置时间窗口约束（三年内至少一次豆类种植），可转化为逻辑表达式嵌入模型。

（2）问题 2：不确定性分析

• 模型扩展：
  • 蒙特卡洛模拟：对销售量、亩产量、价格等参数进行随机抽样，生成多组情景，求解鲁棒解。
  • 鲁棒优化：将参数波动范围转化为约束，寻找在最坏情况下仍可行的最优解。
• 风险控制：
  • 引入 风险价值（VaR） 或 条件风险价值（CVaR） 指标，平衡收益与稳定性。

（3）问题 3：相关性分析

• 模型升级：
  • 多目标优化：考虑作物间的替代 / 互补关系（如蔬菜与食用菌的轮作），构建帕累托前沿。
  • 数据驱动：通过历史数据挖掘价格 - 销量相关性，调整种植策略。

八、参赛心得与实战经验

1. 团队协作策略

• 角色分工：
  • 建模手：负责模型框架设计与理论推导，需快速学习农业领域知识（如轮作制度、作物生长周期）。
  • 编程手：熟练使用 Gurobi/CPLEX 求解优化模型，掌握 Python 的 pandas（数据处理）和 matplotlib（可视化）。
  • 写作手：同步整理思路，确保论文结构清晰（摘要、模型假设、求解步骤、结果分析），避免后期返工。
• 高效沟通：每日召开 15 分钟进度会议，使用 XMind 或 Notion 共享思路，避免信息断层。

2. 时间管理技巧

• 阶段划分：
  • Day 1-2：精读赛题，完成数据清洗与预处理（附件 1-3 数据整合）。
  • Day 3-4：构建基础模型，完成问题 1 的求解。
  • Day 5-6：扩展模型处理不确定性与相关性，生成问题 2-3 的结果。
  • Day 7：论文润色、图表美化、代码检查。
• 风险预案：预留 6 小时应对突发情况（如求解器崩溃、数据格式错误）。

3. 模型优化与创新点

• 简化技巧：
  • 将 34 个地块按类型聚类（如平旱地、水浇地），减少变量维度。
  • 假设豆类作物种植面积占比不低于 10%，简化轮作约束。
• 创新方向：
  • 动态定价模型：对滞销作物采用阶梯式降价策略（如问题 1 (2) 中降价 50%），提升收益。
  • 碳足迹评估：将有机种植的碳排放纳入目标函数，体现可持续发展理念。

九、备战策略与资源推荐

1. 赛前知识储备

• 数学基础：
  • 优化理论：线性规划、整数规划、动态规划（推荐《运筹学》胡运权）。
  • 不确定性分析：蒙特卡洛模拟、鲁棒优化（参考《数学建模算法与应用》司守奎）。
• 工具技能：
  • 编程：Python（核心）+ MATLAB（辅助可视化）。
  • 求解器：Gurobi（学生版免费）、PuLP（开源）。
  • 论文：LaTeX（推荐 Overleaf 在线协作）。

2. 模拟训练计划

• 真题实战：
  • 近五年 C 题：重点练习多目标优化（如 2022 年 “乡村振兴” 题）、动态规划（如 2021 年 “生产调度” 题）。
  • 交叉训练：选择 A/B 题练习数据分析与微分方程建模，拓宽思路。
• 复盘总结：
  • 每完成一题，对比优秀论文，分析模型简化与创新点。
  • 整理常用代码库（如线性规划模板、蒙特卡洛模拟函数）。

3. 资源推荐

• 书籍：
  • 《数学建模竞赛教程》（李尚志）：涵盖历年赛题解析与建模技巧。
  • 《Python 数学建模与数据分析》（张良均）：结合实战案例讲解工具应用。
• 网站：
  • 全国大学生数学建模竞赛官网：获取历年赛题与评审标准。
  • CSDN 数学建模专栏：学习他人解题思路与代码技巧。
• 工具：
  • Gurobi 求解器：高效处理大规模优化问题。
  • Tableau/Power BI：生成动态图表，提升论文可视化水平。

十、避坑指南与注意事项

1. 常见错误与应对

• 模型过拟合：
  • 采用 交叉验证 或 留出法 评估模型泛化能力，避免过度依赖附件数据。
• 计算超时：
  • 简化模型假设（如忽略次要约束），或使用启发式算法（如遗传算法）寻找近似解。
• 论文格式错误：
  • 严格遵循竞赛格式要求（如摘要不超一页、代码放入附录），避免因格式问题扣分。

2. 竞赛心态调整

• 压力管理：
  • 每日保证 6 小时睡眠，团队成员轮流休息，避免疲劳作战。
  • 出现分歧时，以 “模型合理性” 为唯一评判标准，避免情绪化争论。
• 突发情况：
  • 若求解器崩溃，改用 Excel 规划求解 或 Python 的 scipy.optimize 模块应急。

十一、总结与展望

2024 年 C 题的核心在于 “复杂约束下的多目标优化”，要求团队在有限时间内平衡理论深度与工程实用性。通过 模块化建模、分阶段推进、跨学科协作，可有效提升解题效率。建议备赛时注重 工具链整合（如将 Gurobi 与 Python 结合）和 论文写作训练，以应对竞赛中的高强度挑战。