基于kaggle上的新西兰房价预测数据集做一个的房价预测项目。

概要

这一次的项目代码完成了对加州房价数据集的线性回归预测模型的构建和评估过程。

• 首先进行了数据的探索性分析，包括特征的相关性分析和可视化。
• 然后对数据进行了预处理，包括处理缺失值、编码类别特征、独热编码和标准化数值特征。
• 最后使用线性回归模型进行训练，并评估模型的性能。mse和rmse分别表示均方误差和均方根误差，用于评估模型的预测准确度。

项目演示

我们在这里利用，kaggle上的新西兰房价预测数据集做一个入门级的房价预测项目。

技术名词解释

• 独热编码：独热编码是一种在机器学习中用于处理离散型非数值特征的编码方法。独热编码便是其中一种常用的特征数字化方法，它将每个类别特征转换为一个二进制向量，该向量在对应的特征位置上为1，其余位置上为0。
• 缩放数字特征：缩放数字特征是机器学习数据预处理中的重要步骤，它能够提升模型精度和加速收敛速度。
  在机器学习中，数值特征的缩放处理是提高模型性能、加快训练速度的关键步骤。常见的方法包括标准化（Z-score normalization）、最小-最大缩放（Min-Max Scaling）以及使用均值进行归一化等。
• 标准化：标准化（Standardization）是最常用的缩放方法之一，它通过从每个原始数据中减去平均值并除以标准差来实现数据缩放。这种方法将数据转换为均值为0，标准差为1的正态分布。标准化适用于数据集呈正态分布的情况，尤其是当数据具有离群值或者极端值时。标准化后的数据更易于使用基于梯度下降的优化算法，因为它可以显著提高收敛速度和稳定性
• 归一化：使用均值进行归一化（Mean normalization）和缩放到单位长度（Scaling to unit length）也是两种可选的缩放方法。这两种方法较少使用，但在特定情境下仍然有效。例如，如果数据集中的特征已经在同一量纲且相对集中，均值归一化可以快速将数据转换到[-1, 1]区间内。而缩放到单位长度则常用于处理文本数据或任何需要处理向量长度的场景
  （值得注意的是，不同的机器学习模型对特征缩放的需求不同。依赖于距离计算的模型如KNN、K-means、SVM及基于梯度的线性模型和神经网络，特征缩放尤为重要。而对于决策树或随机森林这类基于树的模型，由于其本质上是通过特征的分裂信息增益进行工作，特征缩放对这些模型的影响较小）
• 正则化：正则化是一种提高模型泛化能力、防止过拟合的技术方法。正则化通过在损失函数中添加一个正则项来实现对模型复杂性的控制，从而在保持模型尽量简单的同时，尽可能地拟合数据。具体分为两类：
  L2正则化：也称为岭回归（Ridge Regression），通过对权重向量的L2范数（即欧几里得范数）进行惩罚来限制模型复杂度。L2正则化倾向于使权重值较小但不为零，从而避免模型过于复杂。
  L1正则化：也称为Lasso回归，与L2正则化不同，L1正则化通过对权重向量的L1范数（即权重的绝对值之和）进行惩罚来实现。这会导致一些权重在优化过程中变为零，从而产生一个稀疏模型，具有特征选择的作用。

技术细节（代码演示）

一.数据分析

# 导入所需要的库
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline

接下来导入我们在kaggle上下载的新西兰房价数据集’housing.csv’，（这里有需要的小伙伴可以在后台私信我）

# 导入新西兰房价数据集
from sklearn.datasets import fetch_california_housing
from sklearn.linear_model import LinearRegression
# 真实数据
cal_data = pd.read_csv('housing.csv')
cal_data.describe()

# 查看数据列
cal_data.columns

Index([‘longitude’, ‘latitude’, ‘housing_median_age’, ‘total_rooms’,
‘total_bedrooms’, ‘population’, ‘households’, ‘median_income’,
‘median_house_value’, ‘ocean_proximity’],
dtype=‘object’)

# 查看数据类型
cal_data.dtypes

longitude float64
latitude float64
housing_median_age int64
total_rooms int64
total_bedrooms float64
population int64
households int64
median_income float64
median_house_value int64
ocean_proximity object
dtype: object
这里有关真实数据新西兰房价数据的特征信息

• longitude,经度:房子向西多远的量度;越往西，数值越高
  latitude,纬度:衡量房子往北多远的尺度;越往北，数值越高
  housing_median_age:街区内房屋年龄的中位数;较低的数字代表较新的建筑
  total_rooms:一个街区内的房间总数
  total_bedrooms:一个街区内的卧室总数
  population,人口:居住在一个街区内的总人数
  households,住户:一个街区的住户总数，即居住在一个家庭单位内的一群人
  median_income:街区内住户收入中位数(以万美元计)
  median_house_value:街区内住户的房屋价值中位数(以美元计算)
  oceanProximity:房子靠近海洋/海洋的位置

# 划分数据集，并查看缺失值
from sklearn.model_selection import train_test_split
train_data, test_data = train_test_split(cal_data, test_size=0.1,random_state=20)
#检查数据中的缺失值
train_data.isnull().sum()

二.数据可视化

1.分析特征关系

#检查特征之间的相关性，并进行热力图可视化
correlation = train_data.iloc[:,0:9].corr()#读取0-8列数据
plt.figure()
sns.heatmap(correlation,annot=True,cmap='crest')

#检查特征之间的相关性，并进行热力图可视化
correlation = train_data.iloc[:,0:9].corr()#读取0-8列数据
plt.figure()
sns.heatmap(correlation,annot=True,cmap='crest')

# 根据经度纬度画出经纬度图
plt.figure(figsize=(12,7))
sns.scatterplot(data = train_data, x='longitude', y='latitude')

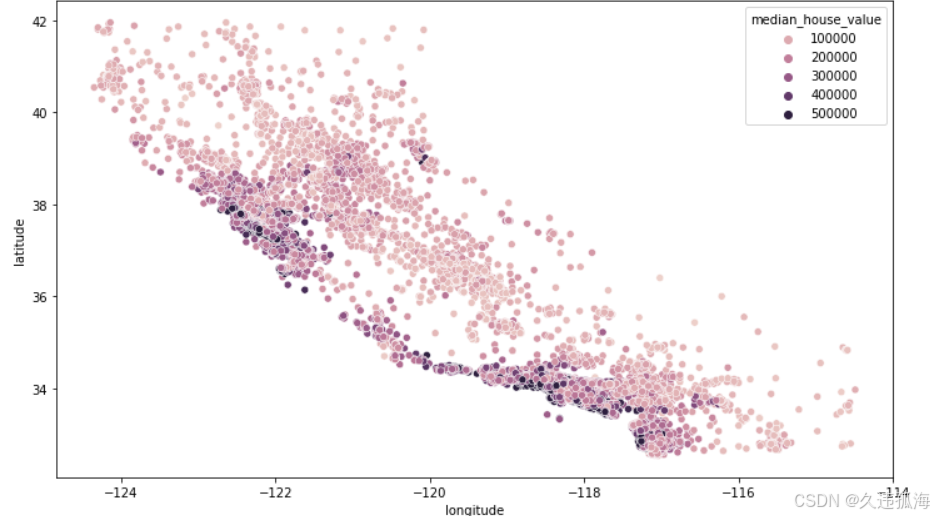
# 绘制地理位置对应的房价中位数的散点图
plt.figure(figsize=(12,7))
sns.scatterplot(data = train_data, x='longitude', y='latitude', hue='median_house_value')

# 绘制沿海地区的经纬度图
plt.figure(figsize=(12,7))
sns.scatterplot(data = train_data, x='longitude', y='latitude', hue='ocean_proximity', 
                size='median_house_value')

三.数据预处理

1.处理缺失值

training_input_data = train_data.drop('median_house_value', axis=1)
training_labels = train_data['median_house_value']

# 处理缺失值
from sklearn.impute import SimpleImputer
num_feats = training_input_data.drop('ocean_proximity', axis=1)
def handle_missing_values(input_data):
  mean_imputer = SimpleImputer(strategy='mean')
  num_feats_imputed = mean_imputer.fit_transform(input_data)
  num_feats_imputed = pd.DataFrame(num_feats_imputed, 
                            columns=input_data.columns, index=input_data.index )
  return num_feats_imputed
num_feats_imputed = handle_missing_values(num_feats)
num_feats_imputed.isnull().sum()

2.编码分类特征

training_input_data['ocean_proximity'].value_counts()

<1H OCEAN 8231
INLAND 5896
NEAR OCEAN 2384
NEAR BAY 2061
ISLAND 4
Name: ocean_proximity, dtype: int64

cat_feats = training_input_data['ocean_proximity']
feat_map = {
      '<1H OCEAN': 0,
      'INLAND': 1,
      'NEAR OCEAN': 2,
      'NEAR BAY': 3, 
      'ISLAND': 4
}
cat_feats_encoded = cat_feats.map(feat_map)
cat_feats_encoded.head()

# 将类别特征独热编码
#海洋邻近特征并不是按任何顺序排列的。通过使用一个热点，将类别转换为二进制表示(1或0)，并将原有的分类特征拆分为更多的特征，相当于类别的数量。
from sklearn.preprocessing import OneHotEncoder
def one_hot(input_data):
    one_hot_encoder = OneHotEncoder()
    output = one_hot_encoder.fit_transform(input_data.values.reshape(-1, 1))
    output = output.toarray()
    return output

cat_feats = training_input_data[['ocean_proximity']]
cat_feats_hot = one_hot(cat_feats)
cat_feats_hot

3.缩放数字特征

# 大多数机器学习模型在给定较小的输入值时都能很好地工作，如果它们在相同的范围内则效果最好。
# 出于这个原因，有两种最常用的技术来扩展功能:
# 1.归一化，将特征缩放到0到1之间的值。和
# 2.标准化，其中特征被重新缩放为具有0平均值和单位标准差。当处理包含异常值的数据集(如时间序列)时，在这种特殊情况下，标准化是正确的选择。

#归一化数值特征
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler()
num_scaled = scaler.fit_transform(num_feats)
#标准化数值特征
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
num_scaled = scaler.fit_transform(num_feats)

# 将所有数据预处理步骤放入单个Pipeline中
# 构建管道处理数值和类别特征
from sklearn.pipeline import Pipeline
from sklearn.compose import ColumnTransformer
num_feats_pipe = Pipeline([('imputer', SimpleImputer(strategy='mean')), ('scaler', StandardScaler()) ])
cat_feats_pipe = Pipeline([('encoder', OneHotEncoder())])
num_list = list(num_feats)
cat_list = list(cat_feats)
final_pipe = ColumnTransformer([
   ('num', num_feats_pipe, num_list),    
   ('cat', cat_feats_pipe, cat_list) ])
training_data_preprocessed = final_pipe.fit_transform(training_input_data)

三.模型评估与优化

# 这里使用sklearn中提供的线性回归模型
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
reg_model = LinearRegression()
#训练模型
reg_model.fit(training_data_preprocessed, training_labels)
predictions = reg_model.predict(training_data_preprocessed)
#评估模型使用 mse 、rmse (MSE（Mean Squared Error）：均方误差，是预测值与实际值之差的平方和的平均值。RMSE（Root Mean Squared Error）：均方根误差，是均方误差的平方根。)
mse = mean_squared_error(training_labels, predictions)
rmse = np.sqrt(mse)
rmse

rmse = 68438.90385283883
这个值不是很理想，我们再一步进行优化。

#使用增加模型的复杂度以提高mse值，多项式特征工程和岭回归模型来提高模型的复杂度
# 使用多项式特征进行特征工程
from sklearn.preprocessing import PolynomialFeatures
poly_features = PolynomialFeatures(degree=2, include_bias=False)
training_data_poly = poly_features.fit_transform(training_data_preprocessed)

# 使用岭回归模型
from sklearn.linear_model import Ridge
ridge_reg = Ridge(alpha=1) # 调整alpha参数以控制正则化程度
ridge_reg.fit(training_data_poly, training_labels)
predictions_ridge = ridge_reg.predict(training_data_poly)

mse_ridge = mean_squared_error(training_labels, predictions_ridge)
rmse_ridge = np.sqrt(mse_ridge)
rmse_ridge

61725.68904483057

# 使用支持向量机回归模型
from sklearn.svm import SVR
svr_reg = SVR(kernel='rbf', C=15, epsilon=0.2) # 调整C和epsilon参数以增加模型的复杂度
svr_reg.fit(training_data_poly, training_labels)
predictions_svr = svr_reg.predict(training_data_poly)

mse_svr = mean_squared_error(training_labels, predictions_svr)
rmse_svr = np.sqrt(mse_svr)
rmse_svr

117211.5622100802

# 使用多项式特征进行特征工程，增加模型的复杂度
poly_features = PolynomialFeatures(degree=2, include_bias=False)
training_data_poly = poly_features.fit_transform(training_data_preprocessed)

# 使用随机森林回归模型
from sklearn.ensemble import RandomForestRegressor
rf_reg = RandomForestRegressor(n_estimators=100, random_state=42) # 调整n_estimators参数以增加模型复杂度
rf_reg.fit(training_data_poly, training_labels)
predictions_rf = rf_reg.predict(training_data_poly)

mse_rf = mean_squared_error(training_labels, predictions_rf)
rmse_rf = np.sqrt(mse_rf)
rmse_rf

最后我们通过不同模型的比较发现随机森林的结果还不错，但还有很大进步空间。

小结

本项目通过构建线性回归模型来预测加州房价数据集中的房价。项目首先进行了数据的探索性分析，包括特征相关性分析和数据可视化，以了解数据的基本分布和特征间的关系。在数据预处理阶段，对缺失值进行了处理，对类别特征进行了编码，并应用独热编码处理非数值特征，以及对数值特征进行了标准化处理，以提升模型性能。模型训练后，使用均方误差（mse）和均方根误差（rmse）作为评估指标，来衡量模型的预测准确度。整个项目流程从数据探索到模型评估，系统地展示了如何使用线性回归模型进行房价预测。