[概率论与数理统计(框框期末速成)] 随机事件及其概率 -- 四大公式

今天也是被数学难到了, 果断不看书就去看b站视频了, 下面是一个简单的分享.

课程链接: 《概率论与数理统计》4小时速成课 | 框框老师（突击课，适合大学数学期末考试、期中考试、补考、重修、专升本，考试不挂科）

本节仅仅介绍一下 [随机事件及其概率] 部分 四大公式.

四大公式是一个俗称, 具体来说是概率加法公式, 减法公式 以及 乘法与条件概率公式(除法公式), 下面来对其一一进行简单介绍.

1. 加法公式

含义: 在概率当中, 我们称"A事件和B事件至少发生一个"这种情况下属于一种概率相加情况.

公式: P(A + B) = P(A) + P(B) - P(AB)

这个加法公式很好理解吧? P(A + B) = P(A) + P(B) - P(AB) 之所以需要额外减去个P(AB), 这是因为P(A) + P(B) 加了两遍.

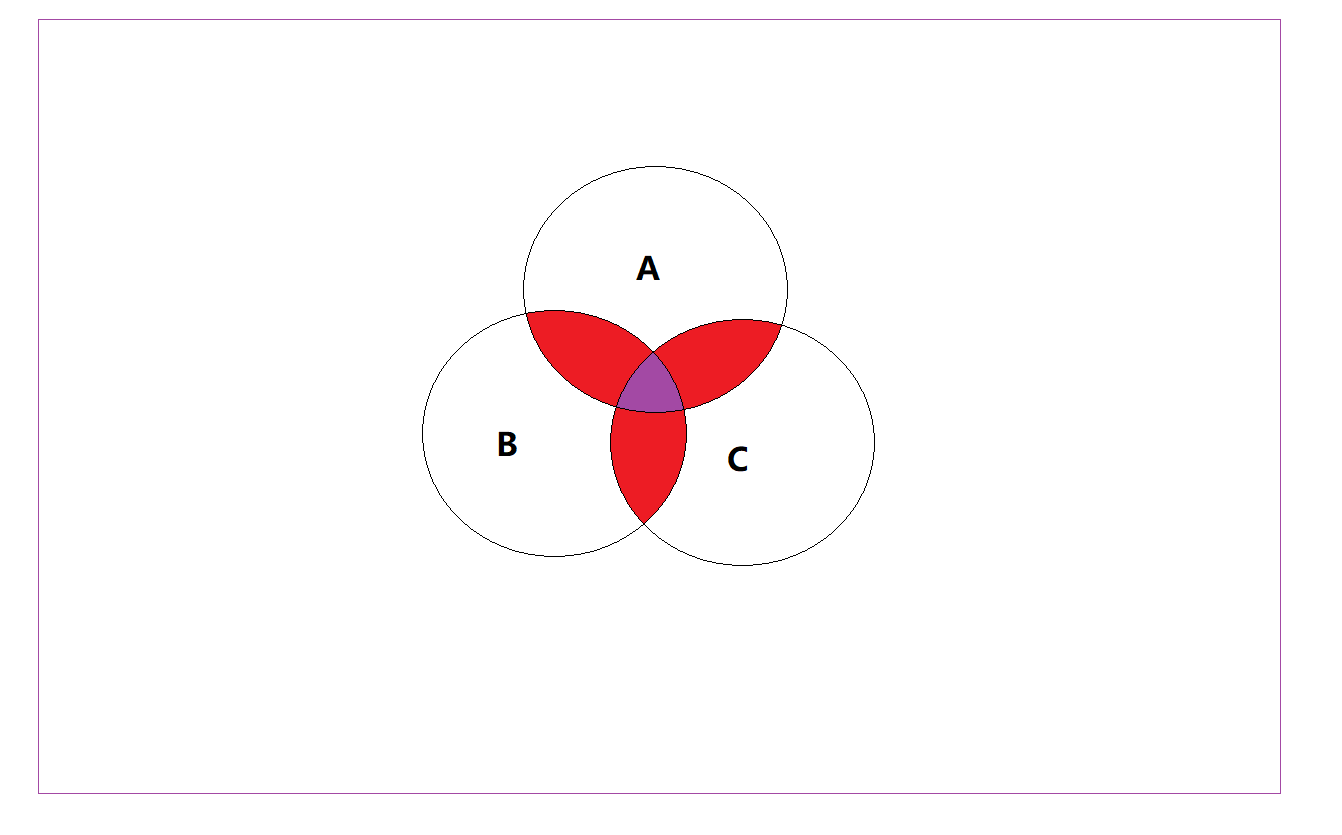
显然, 我们还可以把这个加法公式推广到三个集合中同样适用:

推广公式: P(A + B + C) = P(A) + P(B) + P© - P(AB) - P(BC) - P(AC) - P(ABC)

好的想必大家肯定可以理解, 我们下面简单看一道例题?

例题:
①假设P(A) = 0.5, P(A + B) = 0.8, 并且A, B互不相容, 求P(B).
②假设P(A) = P(B) = P© = 0.25, P(AC) = 0.125, P(AB) = P(BC) = 0, 求A, B, C至少发生一个的概率.

①解: 由于AB互不相容, 换言之, A 与 B是不相交的, 因此, P(AB) = 0. 
P(A + B) = P(A) + P(B) - P(AB)
⇒ P(B) = P(A+B) - P(A) + P(AB)
⇒ P(B) = 0.8 - 0.5 = 0.3. 
②解: 
因为是"至少", 因此求的是P(A + B + C)的值. 
P(A + B + C) = P(A) + P(B) + P(C) - P(AB) - P(BC) - P(AC) + P(ACB). 
⇒ P(A + B + C) = 0.25 + 0.25 + 0.25 - 0 - 0 - 0.125 + P(ACB). 
⇒ ∵ P(ABC) 是 P(AB)的子集, 且 P(AB) = 0, 因此P(ABC) = 0. 
⇒ ∴P(A + B + C)  = 0.25 + 0.25 + 0.25 - 0 - 0 - 0.125 + 0. 
⇒ P(A + B + C)  = 0.625. 

2. 减法公式

含义: 在概率当中, 我们称"P(A−B) 表示事件A发生而事件B不发生的概率"这种情况下属于一种概率相减情况.

公式: P(A - B) = P(A) - P(AB)

我们的推广公式就是:

推广公式: P(AB - C) = P(AB) - P(ABC)

除此之外, 我们还有个对立公式:

对立转换: P(A) = 1 - P(!A)

那下面我们简单做个例题?
例题:
设P(A) = 0.7, P(A-B) = 0.3, 求P(!(AB))

题解: 
P(!(AB)) = 1 - P(AB)
⇒ 因为 P(A - B) = P(A) - P(AB) 
⇒ 即0.3 = 0.7 - P(AB), ∴P(AB) = 0.4
⇒ 因此, P(!(AB)) = 1 - P(AB) = 1 - 0.4 = 0.6. 

3. 独立下的乘法公式 与 条件概率公式(除法公式)

条件概率公式: P(A/B) = P(AB) / P(B), 其中P(B) != 0.
公式2: P(A(!B)) = P(A) - P(AB)

首先, 我们需要解释一下P(A/B)的含义, 即"事件 B已经发生的前提下，事件 A 发生的概率". 同时P(A(!B))的含义是"A发生而B不发生的概率".
那我们再来解释一下公式2为什么成立?
答: 因为:
P(A(!B)) = P(A) - P(AB)
⇒ P(A(!B)) = P(A(1 - B)) = P(A - AB)
⇒ P(A - AB) = P(A) - P(AB).

其中还牵扯到一个概念: 独立.

如果A, B相互独立, 那么P(B/A) = P(B), 同时, P(AB) = P(A) * P(B).

这很好理解吧? P(B/A)的概念就是A发生条件下B发生的概率, 现在A, B两个事件没啥关系了, 肯定只看B发生的概率了~ 然后P(AB)的话含义是"AB两事件同时发生的概率", 如果A, B独立, 那么相乘即可.

我们下面看两道例题:
例1:
假设A, B相互独立, P(B) = 0.4, P(A + B) = 0.5, 求P((!B)/A).
题解1:
P((!B)/A)
⇒ P((!B)A) / P(A)
⇒ (P(A) - P(AB)) / P(A)
⇒ (P(A) - 0.4P(A)) / P(A)
⇒ 0.6P(A) / P(A)
⇒ 0.6.

还有一种题解2:
P((!B)/A)
⇒ 因为独立, 因此P((!B)/A) = P(!B)
⇒ P(!B) = P(1 - B)
⇒ 1 - P(B)
⇒ 1 - 0.4
⇒ 0.6.