计算机科学数学(离散数学)

一.：What is a Proof?

1. 什么是证明？ (What is a Proof?)

• 学生回答 (数学证明的定义): 证明是由一系列陈述构成的链条，每个陈述都由之前的陈述逻辑地支持，最终从一组假设推导出结论。
• 教授赞同: 这个定义非常接近数学证明的定义。
• 更广泛的证明概念: 证明不仅存在于数学中，也存在于其他领域。
• 一般意义上的证明： 一种用于 确证真理 (ascertaining the truth) 的方法。确证真理意味着建立真理、验证真理。

2. 确证真理的不同方法 (Methods for Ascertaining Truth):

• 社会和科学领域中确证真理的例子：
  • 观察与实验 (Observation, Experiment and Observation): 物理学的基础。例如，观察到粉笔会掉落到地面，从而得出重力存在的结论。
  • 证伪 (Establishing Falsehood): 通过证明某些事物是错误的，来缩小真理的范围。
  • 寻找反例 (Counterexamples): 证明某个普遍性陈述是错误的有效方法。
  • 抽样 (Sampling): 通过多次实验或观察，如果结果一致，可以得出结论。
  • 陪审团/法官的裁决 (Juries or Judges): 法律领域中，陪审团或法官通过审查证据来确定事实真相。例子：Roger Clemens 伪证案，OJ Simpson 入室盗窃案。
  • 宗教 (Religion) / 神的旨意 (Word of God): 宗教信仰被视为真理，但解释可能存在争议，依赖于宗教领袖的解读。
  • 老板的指示 (Word of Boss): 在商业环境中，老板的指示通常被视为真理。
  • 教授的权威 (Professor’s Authority): 在课堂上，教授说的内容有时会被认为是真理（教授强调本课程不适用）。
  • 内心确信 (Inner Conviction): 主观感受，例如程序员常有的“我的程序没有 bug”的信念。
  • “我看不出为什么不是真的” (I don’t see why not something is true): 一种转移举证责任的策略，让质疑者承担证伪的责任。
• 数学中的证明 (Mathematical Proof) - 更高级别的定义:
  • 数学证明的定义: 通过 逻辑演绎 (logical deductions) 的链条，从一组 公理 (axioms) 出发，对一个 命题 (proposition) 进行 验证 (verification)。
  • 三个重要组成部分:
    • 命题 (Propositions)
    • 逻辑演绎 (Logical Deductions)
    • 公理 (Axioms)

3. 命题 (Propositions)

• 定义: 一个 陈述 (statement)，它要么 真 (true)，要么 假 (false)。可能不知道真假，但真值是确定的。
  • 简单例子: “2 + 3 = 5” (真命题)
  • 更复杂的例子: “对于所有自然数 n，n² + n + 41 是一个素数” (For all n in the set of natural numbers, n squared plus n plus 41 is a prime number.)
• 符号介绍:
  • “∀” (倒过来的 A): 全称量词 (for all)，表示“对于所有…”。
  • “∈” (属于符号): 表示 “…属于…集合”。
  • “ℕ” (花体 N): 自然数集 (natural numbers)，通常指非负整数集合 {0, 1, 2, 3, …}。
  • 谓词 (Predicate): 一个命题，其真值取决于 变量 (variable) 的值。例子中 “n² + n + 41 是一个素数” 是谓词，变量是 n。
  • 论域 (Universe of Discourse): 讨论范围，即变量可能取值的集合。例子中论域是自然数集 ℕ。
  • 量词 (Quantifier): 指定谓词适用范围的符号。例子中 “∀” 是全称量词。
• 检验命题真假: 需要验证谓词对于论域中 每一个 (every) 值是否都为真。
  • 例子验证: 检验 “n² + n + 41 是一个素数” 对于 n = 0, 1, 2, 3… 是否为真。
    • n = 0, 结果 41 (素数) - 真
    • n = 1, 结果 43 (素数) - 真
    • n = 2, 结果 47 (素数) - 真
    • n = 3, 结果 53 (素数) - 真
    • …
    • n = 39, 结果 1601 (素数) - 真
    • 前 40 个例子都为真，但命题仍然是假的。
• 反例 (Counterexample): 证明命题为假的例子。
  • 反例 n = 40: 40² + 40 + 41 = 1681 = 41² (不是素数)
  • 更明显的反例 n = 41: 41² + 41 + 41 = 41 * (41 + 1 + 1)，能被 41 整除 (不是素数)
  • 结论: 命题 “对于所有自然数 n，n² + n + 41 是一个素数” 是 假 (false) 的。
• 更多命题例子:
  • 费马最后定理的变体 (Euler’s conjecture - counterexample): “a⁴ + b⁴ + c⁴ = d⁴ 没有正整数解” (a to the fourth plus b to the fourth plus c to the fourth equals d to the fourth has no positive integer solutions)。欧拉猜想为真，但后来被证明为假。
    • 反例 (Noam Elkies 发现): a=95800, b=217519, c=414560, d=422481。
    • 正确命题: “存在正整数 a, b, c, d 使得 a⁴ + b⁴ + c⁴ = d⁴” (There does exist a, b, c, d in the positive natural numbers such that a the fourth plus b to the fourth plus c to the fourth equals d to the fourth.)
    • “∃” (倒过来的 E): 存在量词 (there exists)，表示“存在至少一个…”。
    • “ℤ⁺” (Z 上标 +): 正整数集 (positive natural numbers)。
  • 313x³ + y³ = z³ 没有正整数解 (313 x cubed plus y cubed equals z cubed has no positive integer solutions): 实际上是 假 (false) 的，但最小反例非常大，超过 1000 位数。与椭圆曲线和 RSA 加密有关。
  • 四色定理 (Four Color Theorem): “任何地图都可以用四种颜色着色，使得相邻区域颜色不同” (The regions in any map can be colored in four colors so that adjacent regions have different colors)。
    • 历史: 1853 年猜想，1977 年 Appel 和 Haken 用计算机辅助证明，存在争议，近年出现 12 页人工证明但未被完全验证。
  • 哥德巴赫猜想 (Goldbach’s Conjecture): “每个大于 2 的偶数都是两个素数之和” (Every even integer but 2 is the sum of two primes)。
    • 真假未知 (Unknown): 至今未被证明或证伪，数学界难题之一。
    • 《环球报》错误示例: 将 20 = 9 + 11 作为例子 (9 不是素数)。
  • 黎曼猜想 (Riemann Hypothesis): 关于黎曼 Zeta 函数零点的猜想，未解决。
  • 庞加莱猜想 (Poincare Conjecture): 关于三维流形的拓扑性质，已被 Grigori Perelman 于 2003 年证明。
  • 简单整数命题 (Simple Integer Proposition): “对于所有整数 n ≥ 2，n² ≥ 4” (For all integers, n in Z, n greater than or equal to 2 implies n squared is greater than or equal to 4)。
    • “Z” (花体 Z): 整数集 (integers)。
    • “⇒” (单箭头): 蕴含/蕴涵 (implies)，表示 “…蕴含/蕴涵…" 或 “…如果…则…”。
    • 蕴含/蕴涵的真值表 (Truth Table for Implication p ⇒ q):
      • p 真, q 真 => p ⇒ q 真
      • p 真, q 假 => p ⇒ q 假
      • p 假, q 真 => p ⇒ q 真 (假可以蕴含任何真)
      • p 假, q 假 => p ⇒ q 真 (假可以蕴含任何假)
    • **例子: “如果猪会飞，我就是国王” (If pigs could fly, I would be king) - 真命题，因为前提 “猪会飞” 是假的。
      暂时无法在飞书文档外展示此内容
  • 双条件命题 (Biconditional Proposition): “对于所有整数 n ≥ 2，n ≥ 2 当且仅当 n² ≥ 4” (For all integers, n in Z, n greater than or equal to 2 if and only if n squared is greater than or equal to 4)。
    • “⇔” (双箭头): 当且仅当 (if and only if)，表示 “…当且仅当…” 或 “…等价于…”。
    • 双条件命题真值表 (Truth Table for Biconditional p ⇔ q):
      • p 真, q 真 => p ⇔ q 真
      • p 真, q 假 => p ⇔ q 假
      • p 假, q 真 => p ⇔ q 假
      • p 假, q 假 => p ⇔ q 真
    • 反例 n = -3: (-3)² ≥ 4 (真)，但 -3 ≥ 2 (假)。
    • 结论: 命题 “对于所有整数 n ≥ 2，n ≥ 2 当且仅当 n² ≥ 4” 是 假 (false) 的。
• 并非所有句子都是命题 (Not every sentence is a proposition):
  • 非命题例子: “这句话是假的” (This statement is false) - 悖论，既非真也非假。
  • 简单例子: “你好” (Hello) - 不是陈述，既非真也非假。
  • 问题 (Question): “你是谁？” (Who are you?) - 不是陈述，既非真也非假。
  • 本课程主要处理命题。

4. 公理 (Axioms)

• 定义: 一个 被假定为真 (assumed to be true) 的命题。
  • 无需证明: 公理的真假不需证明，直接作为基础假设。
  • 词源: 希腊语 “axioma”，意为 “被认为是值得的”，即认为值得被假定为真。
• 数学中需要假设 (Axioms are necessary in math): 数学需要公理作为逻辑推理的起点。
  • 关键在于明确假设 (Key is to identify assumptions): 数学的关键是明确指出所使用的公理，以便他人理解和验证证明过程。
  • 证明的意义: 任何认同公理的人都必须接受由公理逻辑推导出的结论。
• 公理例子: “如果 a = b 且 b = c，则 a = c” (If a equals b and b equals c, then a equals c) - 传递性公理，无需证明，被普遍接受。
• 不同领域的公理可能矛盾 (Axioms can be contradictory in different contexts): 不同数学体系可以使用不同的公理，甚至互相矛盾。
  • 欧几里得几何 (Euclidean Geometry): “给定一条直线 L 和线外一点 p，存在 唯一一条 通过 p 且平行于 L 的直线” (Given a line L and a point p not on L, there is exactly one line through p parallel to L)。
  • 球面几何 (Spherical Geometry): “给定一条直线 L 和线外一点 p，不存在 通过 p 且平行于 L 的直线” (Given a line L and a point p not on L, there is no line through p parallel to L on the sphere)。
  • 在球面上，“直线” 不是我们通常理解的直线，而是 大圆 (Great Circles)。
  • 在球面上，任意两个大圆都会相交 (Any two great circles intersect)。
  • 想象地球上的两条经线：它们都是大圆，都在南极和北极相交。
  • 因此，在球面上，不存在永不相交的 “直线”。
  • 双曲几何 (Hyperbolic Geometry): “给定一条直线 L 和线外一点 p，存在 无穷多条 通过 p 且平行于 L 的直线” (Given a line L and a point p not on L, there are infinitely many lines through p parallel to L)。
  • 不同几何体系公理的合理性: 不同公理体系在各自的领域内都是自洽的，选择取决于研究对象的性质。
• 公理的指导原则 (Guiding Principles for Axioms):
  • 一致性 (Consistency): 公理集合不能导致矛盾，即不能证明一个命题既真又假。
  • 完备性 (Completeness): 公理集合应该足够强大，能够证明每个命题要么为真，要么为假。
• 哥德尔不完备性定理 (Gödel’s Incompleteness Theorem): Kurt Gödel 在 1930 年代证明，不存在 既 一致 (consistent) 又 完备 (complete) 的公理体系。
  • 意义: 即使在数学中，也存在真理无法被证明。
  • 可能存在无法证明真假的命题 (Undecidable Propositions): 例如，哥德巴赫猜想可能就是一个真命题，但无法被证明。
  • 父母的错误观念: “只要努力工作，就能做到任何事” (If you work hard enough, you can do anything) - 不符合数学的现实。

5. 逻辑演绎 (Logical Deductions) - 简要提及

二.数学归纳法

间接证明：反证法 (Proof by Contradiction)

• 定义： 假设要证明的命题 p 为假，然后进行逻辑推导，直到得到矛盾（“假等于真”）。

• 原理： 如果“非 p 蕴含 假” 为真，那么 p 必须为真。

• 步骤:

  1. 假设“非 p” 为真 (Assume not p is true)。 即假设要证明的命题的否定是成立的。
  2. 逻辑推导 (Logical Deductions)。 从假设出发，进行一系列逻辑推理。
  3. 导出矛盾 (Derive a Contradiction)。 最终推导出与已知事实或前提矛盾的结论（Falsehood is true）。
  4. 结论： p 为真 (Conclude p is true)。 由于假设“非 p” 导致了矛盾，因此“非 p” 必然为假，从而 p 必须为真。

• 示例：证明 √2 是无理数 (Proof that √2 is irrational)

  1. 反证法假设： 假设 √2 是有理数 (Assume √2 is rational)。
  2. 有理数的定义： √2 可以表示为最简分数 a/b，其中 a 和 b 是没有公约数的整数 (√2 = a/b in lowest terms)。
  3. 平方等式： 2 = a²/b² => 2b² = a²。
  4. a² 是偶数 => a 是偶数 (a² is even => a is even)。 因为 a² = 2b²，所以 a² 是偶数。如果 a² 是偶数，那么 a 也必须是偶数。
  5. a 是偶数 => a² 是 4 的倍数 (a is even => a² is multiple of 4)。 如果 a 是偶数，可以写成 a = 2k，那么 a² = (2k)² = 4k²，是 4 的倍数。
  6. 4 | a² 且 a² = 2b² => 4 | 2b² => 2 | b² (4 divides a² and a² = 2b² => 4 divides 2b² => 2 divides b²)。 由于 a² 是 4 的倍数，且 a² = 2b²，所以 2b² 是 4 的倍数，即 b² 是 2 的倍数。
  7. b² 是偶数 => b 是偶数 (b² is even => b is even)。 如果 b² 是偶数，那么 b 也必须是偶数。
  8. 矛盾 (Contradiction)： 我们推导出 a 和 b 都是偶数，这意味着 a/b 不是最简分数，与假设“a/b 是最简分数”矛盾。
  9. 结论：√2 是无理数 (Conclusion: √2 is irrational)。 由于假设“√2 是有理数”导致了矛盾，所以 √2 必然是无理数。

• 历史故事：毕达哥拉斯学派与无理数

  • 古希腊毕达哥拉斯学派认为万物皆数，一切皆可表示为整数或整数之比（有理数）。
  • 无理数的发现（如 √2）冲击了他们的信仰，被认为是“无限”的体现，与代表“有限”和“美好”的神 Peros 相反，与代表“无限”和“邪恶”的神 Apeiron 相关。
  • 传说发现 √2 是无理数证明的学派成员被处死，以保守秘密，维护学派的信仰。
    错误证明示例：90 > 92 (False Proof)

• 利用视觉错觉的错误证明： 通过裁剪和重组三角形，看似将面积为 90 的图形变成了面积大于 92 的图形，从而“证明” 90 > 92。
  

• 错误根源： 图形绘制不精确，视觉上“2 plus”的长度被夸大，导致面积计算错误。

• 教训： 图形证明容易产生误导，精确的数学证明需要严格的逻辑和步骤，而非依赖视觉印象。

• 计算机图形的潜在问题： 屏幕显示可能存在比例失真，进一步加剧视觉误导。
  引入数学归纳法 (Mathematical Induction)

• 数学归纳法的重要性： 计算机科学中最强大、最常用的证明技术。

• 数学归纳法是公理 (Axiom)： 它基于一个被接受为真的基本原则。

• 归纳法公理的陈述:
  设 P(n) 是关于自然数 n 的谓词 (Predicate)。如果：

  1. 基本情况 (Base Case): P(0) 为真 (P(0) is true)。
  2. 归纳步骤 (Inductive Step): 对于所有自然数 n，如果 P(n) 为真，则 P(n+1) 也为真 (For all natural numbers n, P(n) implies P(n+1) is true)。
     那么，对于所有自然数 n，P(n) 都为真 (Then for all natural numbers n, P(n) is true)。

• 多米诺骨牌类比 (Domino Analogy)：

  • P(0) 为真：第一个多米诺骨牌被推倒。
  • P(n) 蕴含 P(n+1)：如果第 n 个多米诺骨牌倒下，则它会推倒第 n+1 个多米诺骨牌。
  • 结论：所有多米诺骨牌都会倒下，即 P(n) 对所有 n 都成立。
    数学归纳法示例 1：证明 1 + 2 + … + n = n(n+1)/2

• 要证明的命题 P(n): 1 + 2 + 3 + … + n = n(n+1)/2，对于所有 n ≥ 0 的自然数。

• “…” 符号的含义 (Meaning of “…”)： 表示根据模式填充中间项，需要谨慎，容易出错。

• 特殊情况 (Edge Cases) 的理解 :

  • n = 1 时，1 + 2 + … + n = 1。
  • n ≤ 0 时，1 + 2 + … + n = 0 （空和，empty sum）。
    

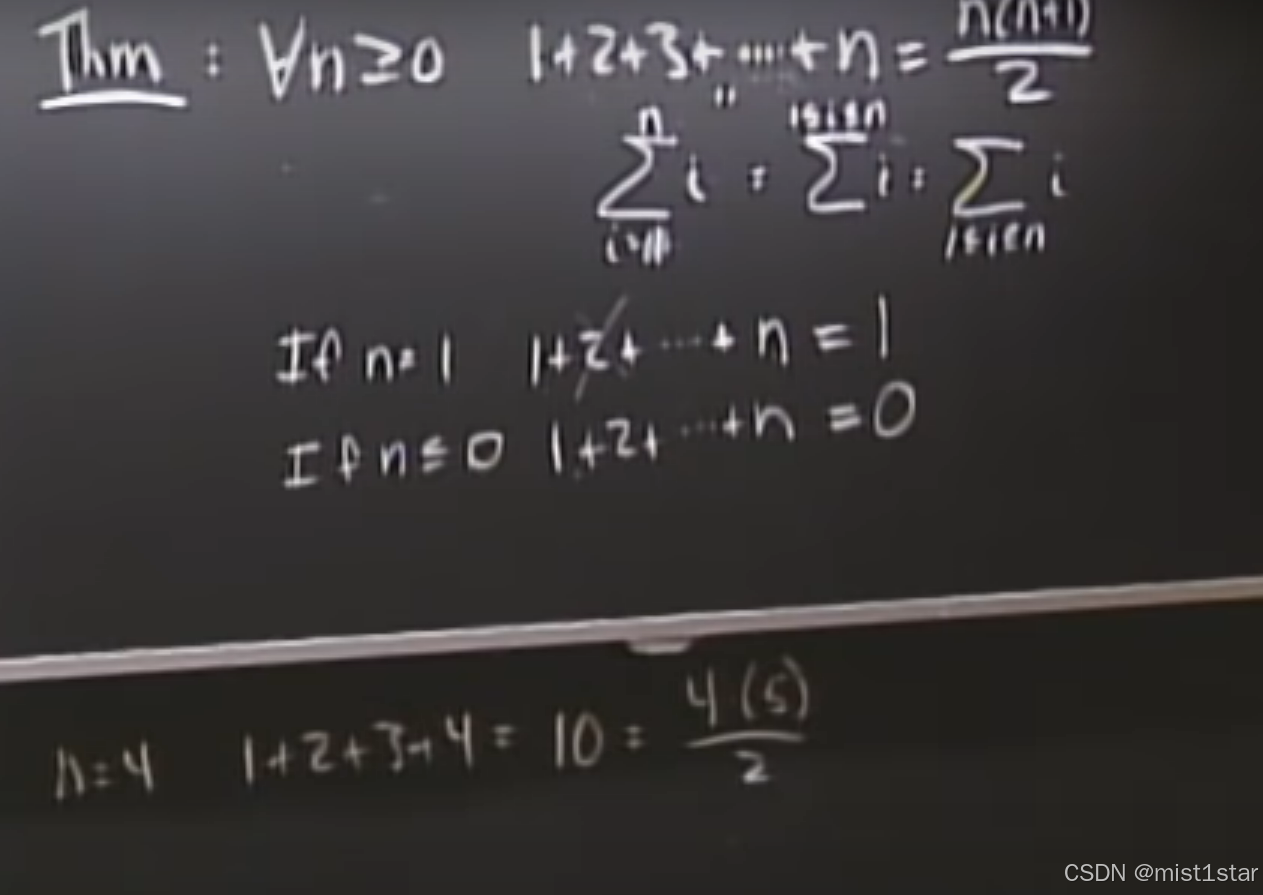
• 归纳证明步骤 ：

  1. 声明： “By Induction” (使用数学归纳法)。
  2. 定义谓词 P(n): 设 P(n) 为 “∑_{i=1}^{n} i = n(n+1)/2”。
  3. 基本情况 (Base Case): 验证 P(0) 为真。
  • ∑_{i=1}^{0} i = 0 (空和为 0)。
  • 0(0+1)/2 = 0。
  • P(0) 为真。
  4. 归纳步骤 (Inductive Step): 假设 P(n) 为真 (归纳假设)，证明 P(n+1) 为真。
  • 假设 P(n) 为真： ∑_{i=1}^{n} i = n(n+1)/2。（由1到n求和）
  • 目标：证明 P(n+1) 为真： ∑_{i=1}^{n+1} i = (n+1)(n+2)/2。
  • 证明过程：
    ∑_{i=1}^{n+1} i = (∑_{i=1}^{n} i) + (n+1) (将和式拆分)
    = n(n+1)/2 + (n+1) (根据归纳假设，替换 ∑_{i=1}^{n} i)
    = (n² + n)/2 + (2n + 2)/2 (通分)
    = (n² + 3n + 2)/2
    = (n+1)(n+2)/2 (因式分解)
  • 结论： P(n) 蕴含 P(n+1) 为真。
  5. 总结： 由于 P(0) 为真，且 P(n) 蕴含 P(n+1)，根据数学归纳法，P(n) 对所有 n ≥ 0 的自然数都成立。

• 归纳法的局限性： 证明了定理的正确性，但没有解释 为什么 定理是正确的，也没有 如何 发现这个公式。归纳法更像验证工具，而非发现工具。
  数学归纳法示例 2：证明 3 整除 (n³ - n)

• 要证明的命题 P(n): 3 | (n³ - n)，对于所有自然数 n。 (3 divides n cubed minus n)

• 示例验证： n = 5 时，5³ - 5 = 120，3 | 120。

• 归纳证明步骤：

  1. 声明： “By Induction”。
  2. 定义谓词 P(n): 设 P(n) 为 “3 | (n³ - n)”。
  3. 基本情况 (Base Case): 验证 P(0) 为真。
  • 0³ - 0 = 0，3 | 0。
  • P(0) 为真。
  4. 归纳步骤 (Inductive Step): 假设 P(n) 为真，证明 P(n+1) 为真。
  • 假设 P(n) 为真： 3 | (n³ - n)。
  • 目标：证明 P(n+1) 为真： 3 | ((n+1)³ - (n+1))。
  • 证明过程：
    (n+1)³ - (n+1) = (n³ + 3n² + 3n + 1) - (n + 1)
    = n³ + 3n² + 2n
    = (n³ - n) + 3n² + 3n
    = (n³ - n) + 3(n² + n)
  • 分析：
    • 根据归纳假设 P(n)，3 | (n³ - n)。
    • 显然 3 | 3(n² + n)。
    • 因此，3 | [(n³ - n) + 3(n² + n)]，即 3 | ((n+1)³ - (n+1))。
  • 结论： P(n) 蕴含 P(n+1) 为真。
  5. 总结： 根据数学归纳法，P(n) 对所有自然数 n 都成立。

• 归纳证明的关键： 在归纳步骤中 必须 使用归纳假设 P(n)。如果没有用到归纳假设，证明很可能存在问题。
  推广：归纳起始点可以不是 0 (42:11-43:04)

• 一般形式的归纳法：

  1. 基本情况： P(b) 为真 (P(b) is true)，其中 b 可以是任意整数。
  2. 归纳步骤： 对于所有 n ≥ b 的整数，P(n) 蕴含 P(n+1) 为真 (For all integers n ≥ b, P(n) implies P(n+1) is true)。
  3. 结论： 对于所有 n ≥ b 的整数，P(n) 为真 (Then for all integers n ≥ b, P(n) is true)。
     错误归纳证明示例：所有马都是同一种颜色 (False Proof - All Horses are the Same Color) (43:04-58:24)

• 错误命题： 所有马都是同一种颜色 (All horses are the same color)。

• 错误归纳证明过程:

  1. 声明： “By Induction”。
  2. 定义谓词 P(n): 在任何包含 n 匹马的集合中，所有马都是同一种颜色 (In any set of n horses, the horses are all the same color)，n ≥ 1。
  3. 基本情况 (Base Case): 验证 P(1) 为真。
  • 在任何包含 1 匹马的集合中，所有马都是同一种颜色 (显然成立)。
  • P(1) 为真。
  4. 归纳步骤 (Inductive Step): 假设 P(n) 为真，证明 P(n+1) 为真。
  • 假设 P(n) 为真： 在任何包含 n 匹马的集合中，所有马都是同一种颜色。
  • 考虑包含 n+1 匹马的集合 H = {h₁, h₂, …, h_{n+1}}。
  • 子集 1： {h₁, h₂, …, h_n}。 根据 P(n)，集合 {h₁, h₂, …, h_n} 中的马颜色相同。
  • 子集 2： {h₂, h₃, …, h_{n+1}}。 根据 P(n)，集合 {h₂, h₃, …, h_{n+1}} 中的马颜色相同。
  • 推理： 由于 h₂ 到 h_n 的马在两个子集中都出现，它们的颜色相同，因此 h₁ 和 h_{n+1} 的颜色也与中间的马颜色相同，从而集合 H 中所有 n+1 匹马颜色相同。
  • 结论： P(n) 蕴含 P(n+1) 为真。
  5. 错误结论： 根据数学归纳法，P(n) 对所有 n ≥ 1 都成立，即所有马都是同一种颜色。

• 错误分析

  • 问题出在归纳步骤，特别是 n = 1 时，P(1) => P(2) 的推导。
  • 当 n = 1 时，子集 1 为 {h₁}，子集 2 为 {h₂}。它们的交集为空集，无法建立 h₁ 和 h₂ 颜色相同的联系。
  • “…” 符号的误导： 在 n=1 时，{h₂, h₃, …, h_n} 实际上是空集，但在证明中被误认为是包含 h₂ 到 h_n 的集合。
  • 缺失的环节： 虽然证明了 P(n) => P(n+1) 对于 n ≥ 2 成立，但 没有 证明 P(1) => P(2) 成立。
  • 基本情况的重要性： 即使归纳步骤看似正确，如果基本情况或关键的归纳步骤（如 P(1) => P(2)）不成立，整个证明就是无效的。

• 修正错误 :

  • 如果从 P(2) 开始作为基本情况，则 P(2) 显然为假 (存在两匹颜色不同的马)。 因此，无法通过归纳法证明所有马颜色相同。
  • 错误证明实际上证明了： 如果任意两匹马颜色相同，则所有马颜色相同。这个条件本身就是假的。
    数学归纳法示例 3：L 型瓷砖铺设问题 (L-Shaped Tile Problem)

• 问题背景： 为史塔特中心（Stata Center）庭院铺设 L 型瓷砖，中间留一个位置给雕像。

• L 型瓷砖： 由三个正方形组成的 L 形。

• 目标： 证明对于任意 n，存在一种方法用 L 型瓷砖铺满 2^n x 2^n 的区域，中心位置空出一个方块。

• 初始尝试 :

  • 命题 P(n)： 存在一种方法用 L 型瓷砖铺满 2^n x 2^n 的区域，中心方块空出。
  • 基本情况 P(0)： 1x1 区域，即中心方块，无需瓷砖，成立。
  • 归纳步骤： 将 2^(n+1) x 2^(n+1) 区域分成四个 2^n x 2^n 区域。
  • 问题： 直接应用归纳假设 P(n) 无法解决中心方块的问题，因为四个子区域的中心都在大区域的四分之一处，而非大区域的中心。

• 改进方案 1：角方块空缺 (Corner Square Missing)

  • 修改命题 P(n)： 存在一种方法用 L 型瓷砖铺满 2^n x 2^n 的区域，角方块 空出。
  • 归纳步骤：
    1. 将 2^(n+1) x 2^(n+1) 区域分成四个 2^n x 2^n 区域。
    2. 在大区域的中心放置一个 L 型瓷砖，使其覆盖四个子区域的中心交汇处。
    3. 这样每个子区域都 缺少一个角方块 （被 L 型瓷砖占据了一个角）。
       每个缺少的角方块就相当于每个2^n中心的雕像
    4. 对每个子区域应用归纳假设 P(n)，即可完成铺设。
       假设P(n)成立去证明P(n+1)成立
  • 结论： 证明了可以铺设 角方块 空缺的 2^n x 2^n 区域。
  • 进一步推导 ： 利用角方块空缺的结论，可以将中心方块空缺的问题转化为角方块空缺问题，从而解决最初的目标。

• 改进方案 2：任意方块空缺 (Any Square Missing) (更简洁的方法)

  • 进一步加强命题 P(n)： 存在一种方法用 L 型瓷砖铺满 2^n x 2^n 的区域，任意一个方块 空出。 (更强的归纳假设)
  • 归纳步骤：
    1. 将 2^(n+1) x 2^(n+1) 区域分成四个 2^n x 2^n 区域。
    2. 根据要空出的方块 Bill 的位置，确定 Bill 所在的子区域。
    3. 在大区域的中心放置一个 L 型瓷砖，使其覆盖 另外三个 子区域的中心交汇处。
    4. 这样，每个子区域都缺少一个方块 （Bill 所在的子区域缺少 Bill 的位置，另外三个子区域缺少被 L 型瓷砖覆盖的位置）。
       
    5. 对每个子区域应用归纳假设 P(n)，即可完成铺设。
  • 结论： 证明了可以铺设 任意方块 空缺的 2^n x 2^n 区域，自然也包括中心方块空缺的情况。

• “更强的归纳假设” 的威力 :

  • 看似更难证明的命题（任意方块空缺）反而更容易通过归纳法证明。
  • 更强的归纳假设 P(n) 提供了更强大的工具，使得归纳步骤 P(n) => P(n+1) 更容易实现。
  • 原则：如果第一次归纳不成功，尝试证明更强的命题 (If you don’t succeed at first, try something harder)。