数据结构教程复数的具体表示和四则运算（加减乘除）（详解）

数据结构教程第六版第十四页例题扩展

2024-03-02知识总结：利用结构体和函数进行有关复数的具体表示，加减乘除（四则运算）和取模，以及new和delete的用法，空间创建和销毁

凌乱是个懒人，上课本是最简单的，以此为例来写复数的表现形式和加减乘除，取模

这里使用c++进行演示，利用引用（别问，问就是二级指针我不会）（当然这里使用二级指针亦可解题）

1.首先是c++头文件

由于接下来我们即将利用c++来编写程序，所以有必要给大家介绍一下c++的头文件，这里只是一笔带过，想看更加详细的解释，请看我之前的博客：

初学c++小白讲解与见解

C++ 中有很多标准头文件，每个头文件都提供了不同的函数和数据类型。以下是一些常用的头文件及其用法：（以下内容收集于网络，老实说有些我也没学到，但是跟C没什么区别）

<iostream>：输入输出流，提供输入输出功能，如 cout 和 cin，用于屏幕输入和输出。

<cmath>：提供数学函数，如三角函数、对数、指数和幂函数等以及开根号等内容。

<cstdlib>：提供与 C 标准库有关的函数，如内存管理和随机数生成等。

<ctime>：提供与时间有关的函数，如获取当前时间和计时等。

<cstring>：提供与字符串有关的函数，如字符串比较和复制等。

<cstdio>：提供与标准输入输出有关的函数，如 printf 和 scanf。

<fstream>：提供文件输入输出功能，如读写文件等。

<iomanip>：提供格式化输出功能，如设置输出精度和宽度等。

<string>：提供字符串类型和与字符串有关的函数，如字符串拼接和查找等。

<vector>：提供向量类型和与向量有关的函数，如向量元素的访问和添加等。

<algorithm>：提供各种算法，如排序、查找和操作等。

<queue>：提供队列类型和与队列有关的函数，如入队和出队等。

<stack>：提供栈类型和与栈有关的函数，如入栈和出栈等。

<map>：提供映射类型和与映射有关的函数，如添加和查找映射元素等。

<set>：提供集合类型和与集合有关的函数，如添加和查找集合元素等。

目前我自己用得多的是<algorithm>头文件，其中的函数大多数都是模板函数，可以用于处理各种类型的容器和数组。也收集了一些常用到的函数：

sort：用于对容器中的元素进行排序。

find：用于在容器中查找指定元素，并返回其迭代器。

count：用于计算容器中某个元素的个数。

replace：用于替换容器中的某个元素为另一个元素。

merge：用于合并两个已排序的容器。

reverse：用于翻转容器中的元素。

transform：用于将一个容器中的元素转换为另一种类型的元素，并存储到目标容器中。

max_element/min_element：用于查找容器中最大/小的元素，并返回其迭代器。

accumulate：用于对容器中的元素进行累加或累乘操作。

fill：用于将容器中的元素全部置为指定的值。

        至于使用`using namespace std`的主要作用是引入标准命名空间`std`中的所有标识符，使得程序可以直接使用这些标识符，而不需要加上`std::`前缀。这可以简化代码，提高编程效率。例如，使用`std::cout`而不是`cout`，使用`std::vector`而不是`vector`。

2.好了下一个部分复数的表示

首先吧，我们打算实现复数的表示，何为复数，实数x的几何表示是x轴上的点，所以称为x轴为实轴；纯虚数i y对应y轴上的点，所以称为y轴是虚轴；复数则表示了所有实轴、虚轴、和复平面上的所有点；（其实大家都学过，这里不赘述）

那么第一步：复数的表示我们会遇到

a: 虚实部都为0, b: 结果只有实部 ,c:结果只有虚部，d：结果的实部虚部都有

所以在表示的时候我们需要注意上述4种情况以及特判1

我们知道如果虚部为1，则表示成i而非1i，所以这种情况我们也需要考虑

具体实现方法如下

#include<iostream>
using namespace std;
typedef struct
{
	double num;
	double i;	
}Complex;
//初始化
void Initcomplex(Complex *&z)
{
	z=new Complex;//开辟一个新空间，值得一提的是每个结构体在定义的时候是没有空间的，所以需要手动开辟
}
//构造
void assigncomplex(Complex *&z,double a,double b)
{
	Initcomplex(z);
	z->num=a;//z->num这句表示给z结构体的成员num赋值a
	z->i=b;
}
//输出
void discomplex(Complex *z)
{
	if(z->i==0||z->num==0)//判断是否有0
	{
		if(z->i==0&&z->num!=0)//数字可以为1
		{
			cout<<z->num;
		}
		else if(z->i!=0&&z->num==0)//虚部排除1
		{
			if(z->i==1)	cout<<"i";
			else if(z->i==-1)	cout<<"-i";
			else	cout<<z->i;
		}
		else //都为0则为0
		{
			cout<<0;
		}
	}
	else if(z->i>0)//虚部大于0
	{
		if(z->i==1)
			cout<<z->num<<"+"<<"i"<<endl;
		else
			cout<<z->num<<"+"<<z->i<<"i"<<endl;
	}
	
	else//虚部小于一
	{
		if(z->i==-1)	
			cout<<z->num<<"-"<<"i"<<endl;
		else	
			cout<<z->num<<z->i<<"i"<<endl;
	}
} 
int main() 
{
	double a,b,c,d;
	cout<<"请输入第一个复数的实部";cin>>a;	
	cout <<"请输入第一个复数的虚部";cin>>b;
	Complex *z1;//定义一个指向结构体的z1,注意这时候他没有空间，准确来说，类似于指针，没有初始化；
	assigncomplex(z1,a,b);//值得一提，里面包含Initcomplex
	cout<<"第一个复数的表示为：";discomplex(z1);cout<<endl;
	cout<<"请输入第二个复数的实部";cin>>c;	
	cout <<"请输入第二个复数的虚部";cin>>d;
	Complex *z2;//2
	assigncomplex(z2,c,d);
	cout<<"第二个复数的表示为：";discomplex(z2);cout<<endl;
	return 0;
}

其实不难的，把该考虑的考虑一下就行

3.接下来加减乘除和取模（就不再解释了，有注释的）

tips：

复数的加法运算：实部+实部，虚部+虚部

复数的减法运算：实部-实部，虚部-虚部

复数的乘法运算：（a1+b1i)*(a2+b2i)=a1*a2+a1*b2i+a2*b1i+b1*b2i^2 (就是简单的相乘）

复数的除法运算：（a1+b1i)/(a2+b2i)：这两个多项式分别乘以第二个多项式的共轭式：（a2-b2i）

pow函数是用于计算某个数的平方

#include<iostream>
#include<cmath>//相当于#include<math.h>,其实这里使用math.h亦可（因为c++兼容c），不过写c++嘛，入乡随俗
using namespace std;
typedef struct
{
	double num;
	double i;	
}Complex;
//初始化
void Initcomplex(Complex *&z)
{
	z=new Complex;
}
//构造
void assigncomplex(Complex *&z,double a,double b)
{
	Initcomplex(z);
	z->num=a;
	z->i=b;
}
//输出
void discomplex(Complex *z)
{
	if(z->i==0||z->num==0)//判断是否有0
	{
		if(z->i==0&&z->num!=0)//数字可以为1
		{
			cout<<z->num;
		}
		else if(z->i!=0&&z->num==0)//虚部排除1
		{
			if(z->i==1)	cout<<"i";
			else if(z->i==-1)	cout<<"-i";
			else	cout<<z->i;
		}
		else //都为0则为0
		{
			cout<<0;
		}
	}
	else if(z->i>0)//虚部大于0
	{
		if(z->i==1)
			cout<<z->num<<"+"<<"i"<<endl;
		else
			cout<<z->num<<"+"<<z->i<<"i"<<endl;
	}
	
	else//虚部小于一
	{
		if(z->i==-1)	
			cout<<z->num<<"-"<<"i"<<endl;
		else	
			cout<<z->num<<z->i<<"i"<<endl;
	}
} 
//加法
void Add(Complex *z1,Complex *z2,Complex *&s)
{
	s->num=z1->num+z2->num;
	s->i=z1->i+z2->i;
}
//减法
void dfr(Complex *z1,Complex *z2,Complex *&sub)
{
	sub->num=z1->num-z2->num; 
	sub->i=z1->i-z2->i;
}
//乘法
void product(Complex *z1,Complex *z2,Complex *&mul)
{
	double num,i;
	num=z1->num*z2->num-z1->i*z2->i;
	i=z1->i*z2->num+z1->num*z2->i;
	mul->num=num;mul->i=i;
	
}
//除法
void did(Complex *z1,Complex *z2,Complex *&dd)
{
	if(z2->num==0&&z2->i==0)
	{
		cout<<"Error:无法计算商，因为除数即第二个复数为0,无意义！！！"<<endl;
	}
	else{
	dd->num=(z1->num*z2->num+z1->i*z2->i)/(z2->num*z2->num+z2->i*z2->i);
	dd->i=(z1->i*z2->num-z1->num*z2->i)/(z2->num*z2->num+z2->i*z2->i);	
	}
}
//取模
void qumo(Complex *z1,double &mo)
{
	mo=sqrt(z1->num*z1->num+z1->i*z1->i);
	
}

int main() 
{
	double a,b,c,d;
	cout<<"请输入第一个复数的实部";cin>>a;	
	cout <<"请输入第一个复数的虚部";cin>>b;
	Complex *z1;//定义一个指向结构体的z1,注意这时候他没有空间，准确来说，类似于指针，没有初始化；
	assigncomplex(z1,a,b);//值得一提，里面包含Initcomplex
	cout<<"第一个复数的表示为：";discomplex(z1);cout<<endl;
	cout<<"请输入第二个复数的实部";cin>>c;	
	cout <<"请输入第二个复数的虚部";cin>>d;
	Complex *z2;//2
	assigncomplex(z2,c,d);
	cout<<"第二个复数的表示为：";discomplex(z2);cout<<endl;
	//加
	Complex *s;Initcomplex(s);//3
	Add(z1,z2,s);
	cout<<"他们的和为：";discomplex(s);cout<<endl;
	//减
	Complex *sub;Initcomplex(sub);//subtract(sub)//4
	dfr(z1,z2,sub);
	cout<<"他们的差为：";discomplex(sub);cout<<endl;
	//乘
	Complex *mul;Initcomplex(mul);//multiply(mul)//5
	product(z1,z2,mul);
	cout<<"他们的乘积为：";discomplex(mul);cout<<endl;
	//除法
	Complex *dd;Initcomplex(dd);//divide(dd)//6
	did(z1,z2,dd);
	
	if(z2->num!=0||z2->i!=0){
		cout<<"他们的商为：";
		discomplex(dd);cout<<endl;
	}
	//取模
	double mo;
	qumo(z1,mo);
	cout<<"第一个复数的模是："<<mo<<endl;
	qumo(z2,mo);	cout<<"第二个复数的模是："<<mo;
	//销毁：可以知道需要消灭7个new分配的空间，类型是结构体
	delete z1;delete z2;delete sub;delete mul;delete dd;
	return 0;
}

这就是我的蒟蒻代码，如果有错，请各位大佬指出！（膜拜）

return ok；

接下来是测试步骤

样例第一组6-i，5+3i；

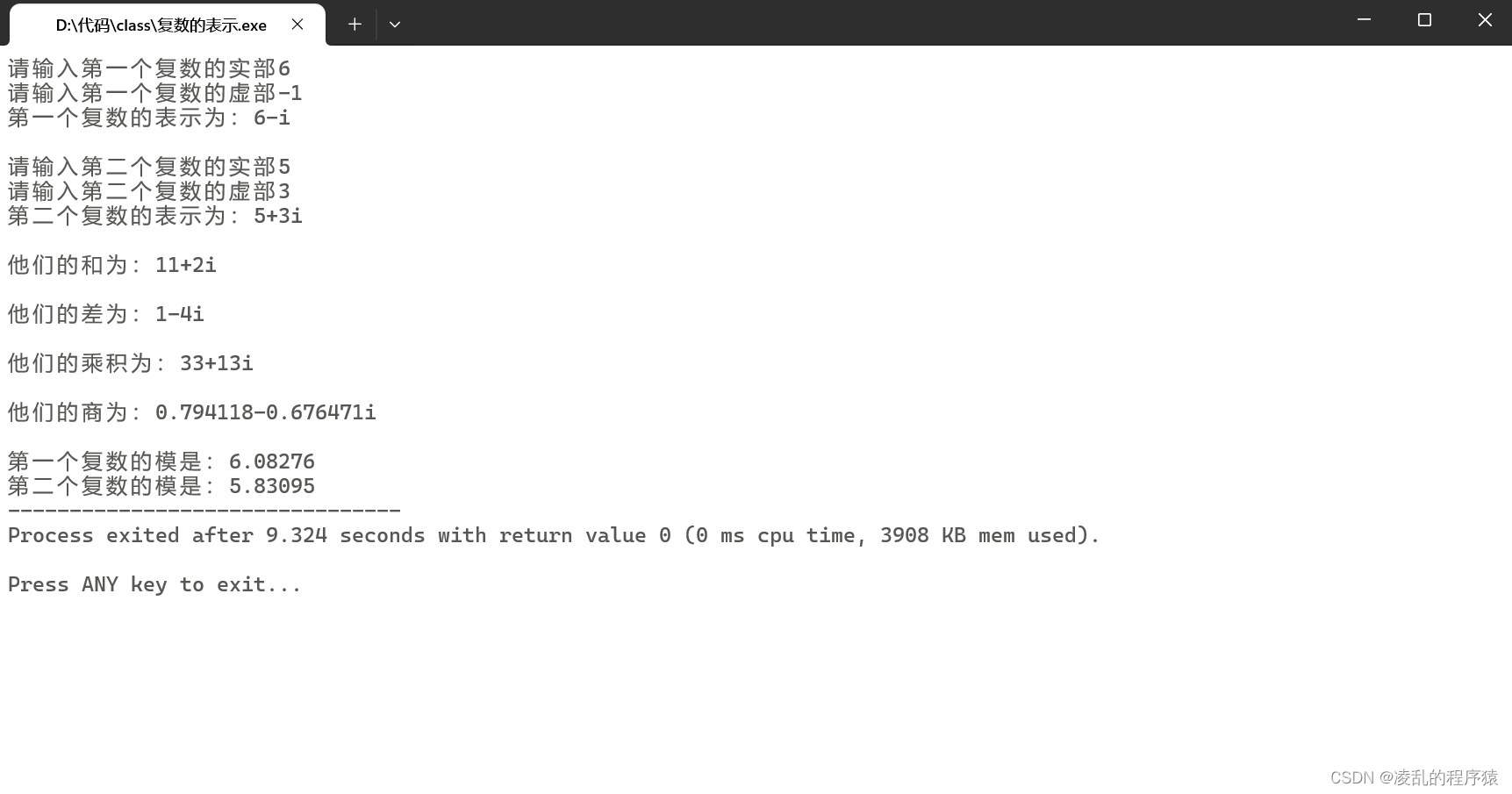
第二组5，0

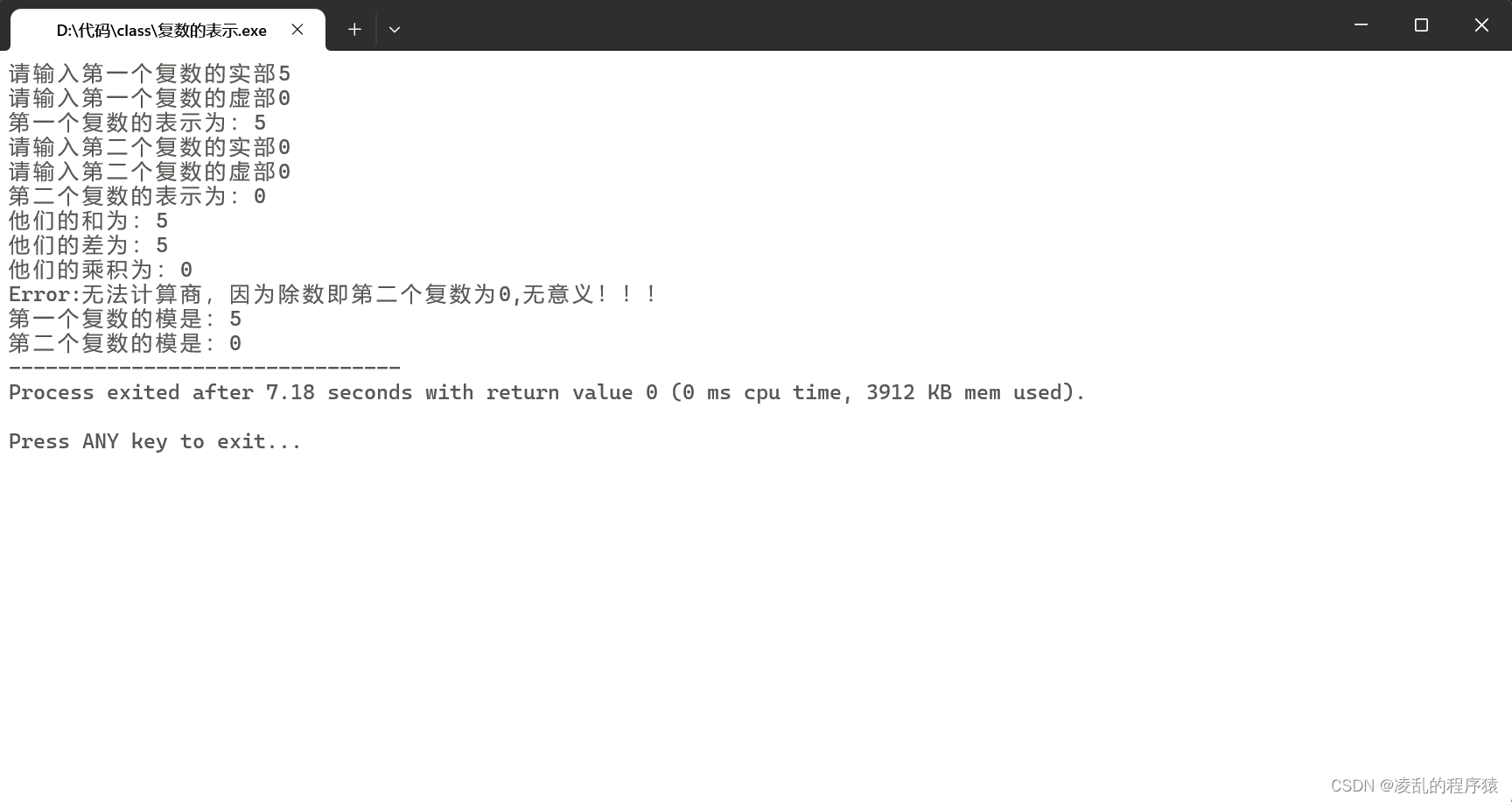
ok啦走了！！