【python 模拟卷A实操题16 机器人集合】全国高校计算机能力挑战赛

这里提供一些选择题知识点整理

• 全国高校计算机能力挑战赛选择题知识点整理

16、机器人遍历最小值

原题

• 集合位置多个机器人分布在M*N(10≤M,N≤1000)的方格中,一个方格可能有多个机器人。
• 规定每个机器人只能向上下左右的相邻方格移动,每移动一个方格需要消耗1个单位能量。
• 现在要求所有机器人集合,集合点只能是某个机器人初始所在方格。现在请找一个集合点,使得所有机器人到达该点消耗的总能量最低。
• 输入说明:第一行是一个整数K(0<K≤100),表示有机器人的方格数量。之后K行表示初始状态有机器人的方格位置(x,y|1≤x<M,1≤y<N)和方格内的机器人数量n,以空格隔开。

输出没有说明，猜测要最佳目标点和最低能量
格式可能是列表，可能有其他要求

读题：

1.取值范围

10≤M,N≤1000

不涉及数值溢出
也就是可以暴力的把每一个都算一遍，然后找出最小的那个，也就是用遍历

整数K(0<K≤100)

整数范围之内，不需要特殊处理

(x,y|1≤x<M,1≤y<N)

同理，没超过int

2.能量计算规则

规定每个机器人只能向上下左右的相邻方格移动,每移动一个方格需要消耗1个单位能量。

只能上下左右相邻方格移动情况下的最短路径，就是小学数学的数格子
数一数纵向的距离，再数一数横向的距离
如图

• 假设有两个点
• A是目标位置
• N是当前位置
• 他们并不重合
• 我们要计算两者之间的距离是多少

从N出发到与A齐平，一格一格往前数，是6步
从转折位置向左走，总共是10步

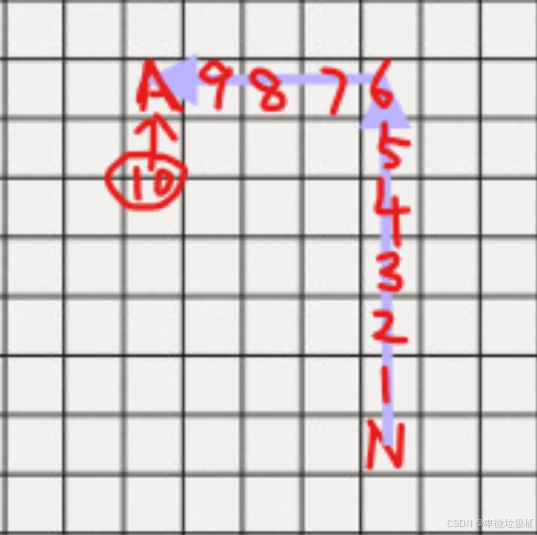
,每移动一个方格需要消耗1个单位能量。

也就是说，刚才从N到A一共走了10步，一步一个能量，就是10能量

一个方格可能有多个机器人

说明一些点会重合
假如N上有两个机器人
那么N到A的路程就会被走两次，我们在计算总共的距离时，需要将这个点的路程*2

以此类推
其他点以此类推

所有步的相加，就是所有机器人到目标的能量
这里不需要用列表

3.计算范围

集合点只能是某个机器人初始所在方格

这里限定范围，范围是所有机器人的初始位置

所有机器人到达该点消耗的总能量最低。

输出条件是总能量最低
也就是说，我们要遍历所有点到目标点的距离
因为最后我们不涉及排序，不涉及比较，
最后只保留计算后的值，在最后保留数值就OK

4.输入输出格式

第一行是一个整数K(0<K≤100),表示有机器人的方格数量

输入一个K，不涉及数值溢出
可以直接用K=int(input())

之后K行表示初始状态有机器人的方格位置(x,y|1≤x<M,1≤y<N)和方格内的机器人数量n,以空格隔开。

输入一行数据 第一个是机器人所在的横坐标，第二个机器人所在的是纵坐标，第三个是机器人数量
这里要用列表输入，列表命名为rb，robots机器人。
后续坐标需要单独提出来，放在新的列表里面，命名为rbP，robots point

总结

1. 取值范围

• 都在int的范围内
• 对于遍历没有影响

2. 计算方式

   1. 获得坐标，机器人数
   2. 设计切换目标点的代码
   3. 计算每个点到目标位置的x坐标和y坐标，然后加和
   4. 如果一个点上有两个机器人，要把路径乘两遍，有3个就乘3遍
   5. 判断只不是最小距离，并选择要不要储存
   6. 输出最小值
   7. 计算涉及（x，y，n）三个数值，代表横坐标，纵坐标，和机器人数

3. 输入与输出

   1. 系统输入一个K
   2. 系统输入一行（x,y,n）代表横坐标，纵坐标，和机器人数，使用列表，列表命名为rbP，也就是robot positions机器人位置的简写

代码实现

从计算条件开始，最后处理输入条件
代码全貌

def get_min(rbP):
    # 初始化能量最小值，使用 float('inf') 作为初始最大值
    minE = float('inf')

    # 初始化最佳目标点，设置为 None，因为稍后将存储一个坐标元组
    bestP = None

    # 遍历每一个可能的集合点
    for p in rbP:
        # 提取当前候选集合点的坐标 (aimX, aimY)
        aimX, aimY, _ = p

        # 初始化总能量为 0
        totalE = 0

        # 遍历所有机器人位置，计算到当前目标点的距离，并加权累加到 totalE 中
        for (x, y, n) in rbP:
            totalE += (abs(x - aimX) + abs(y - aimY)) * n

        # 如果当前计算出的总能量小于之前的最小能量，则更新最小能量和最佳目标点
        if totalE < minE:
            minE = totalE
            bestP = (aimX, aimY)

    # 返回最低能量消耗和最佳目标点的位置
    return minE, bestP

# 从用户输入获取 K 的值，即要处理多少个机器人位置数据
K = int(input())

# 初始化空列表用于存储所有机器人位置数据
rbP = []

# 循环读取 K 行输入，每行包括 x, y 和 n，然后添加到 rbP 列表中
for _ in range(K):
    x, y, n = map(int, input().split())
    rbP.append((x, y, n))

# 调用函数并输出结果
resE, bestP = get_min(rbP)
print(resE, bestP)

1. 函数的详细解释

定义函数

#	定义函数get_min以获得最小值，将读入的数据列表rbP 放进计算方式里
def get_min(rbP):

初始化值

# 初始化能量最小值,energy min 所以命名minE
# float('inf')是python内置的最大值，float('inf')就是最小值，写None也可以但是后续要加条件，推荐用 float('inf')
	minE=float('inf')
#	初始化最佳目标点，也就是最佳路径点  best position 也就是bestP，这里只能写None，因为这里之后是存列表的，不是存值的
	bestP=None

遍历每一个目标点

	for p in rbP:	
#	把xy拿出来，命名为目标xy aimX，aimY，然后给机器人数量一个变量防止报错
#python可以多个变量同时命名

进行初始化

	aimX,aimY,_=p
#	初始化计算所有点到当前目标点的距离，命名totalE，也就是toatal energy总共的能量
	totalE =0

算所有的点到目标点的距离，并把重复的路径多乘，最后得到totalE

	for(x,y,n） in rbP:

写计算流程

#		abs 求绝对值
#		x， y分开计算，因为不能让机器人走斜线
#		abs 是绝对差，就是当前x到目标x的距离
		totalE+=sum(abs(x-aimX)+abs(y-aimY))*n
		if totalE <minE :
		minE=totalE
		bestP=(aimX,aimY)		

算出totalE之后判断和minE的相比，totalE是多还是少，如果少就赋值给minE，minE的赋值是无限大，所以不需要考虑初始要不要多加条件去处理

然后储存当前目标点，要以元组的形式储存，因为看起来更好看
并且题目没有给输出格式，所以我们默认用最好看的模式输出

之后跳出循环，并返回以上操作后的最低点和最低能量

	return minE bestP

1. 输入的详细解释

单纯K输入

# 从用户输入获取 K 的值，即要处理多少个机器人位置数据
K = int(input())

初始化数值，做空列表

# 初始化空列表用于存储所有机器人位置数据
rbP = []

空列表不能直接读输入的数据
因为会变成读了一行字符串，后期还要拆分，然后再次操作变成整数

# 循环读取 K 行输入，每行包括 x, y 和 n，然后添加到 rbP 列表中
for _ in range(K):
    x, y, n = map(int, input().split())
    rbP.append((x, y, n))

最后初始化结果·，并输出
这会输出两个值

# 调用函数并输出结果
resE, bestP = get_min(rbP)
print(resE, bestP)

print(get_min(rbP)）会直接输出一个元组