在之前的章节,我们学习了堆的具体概念和用法,那么本章节,我们来讨论一下堆的复杂度问题,能够更加形象的展现堆结构算法的一些区别,希望大家认真对待。
目录
堆中层数和节点的关系
1.满二叉树
先复习一下结构图
满二叉树的最后一层是满的。

我们很清楚满二叉树,层数和每层的节点是等比数列的关系
第一层有2^0个节点
第二层有2^1个节点
第三层有2^2个节点
...
第n层有2^(n-1)个节点
我们设高度为h,节点个数为N
F(h)是h层以上的节点的函数
F(h)= ,很显然这个函数是一个等比数列,我们利用等比数列求和公式,可以得出
F(h) = = N,再利用对数变形可以得到N和h的关系,即:
2.完全二叉树
先复习一下结构图

完全二叉树节点最多的情况就是满二叉树
我们只需要计算节点最少的情况,即

很显然,根据满二叉树我们推算的结论
完全二叉树节点最少情况为
F(h) =
根据等比数列求和公式,我们可以得出
F(h) =
再进行变形得出N和h的关系
以上就是满二叉树和完全二叉树中,层数和节点的关系
建堆算法的时间复杂度
向下调整建堆算法的时间复杂度
由于时间复杂度是讨论最差的情况,所以向下调整就是每个节点都需要向下调整,直至到叶结点

我们假设有h层,一共N个节点,我们根据上图可以看到,
h-1层,需要向下调整1次
h-2层,需要向下调整2次
...
1层,最差需要向下调整h-1次
我们在根据节点数进行总结
第一层,有个节点,需要向下移动h-1层
第二层,有个节点,需要向下移动h-2层
...
第h-1层,有个节点,需要向下移动1次
所以我们可以进行计算
T(h) = 2^0*(h-1)+2^1*(h-2)+2^2*(h-3)+2^3*(h-4)+...+2^(h-2)*1 (1)
我们可以利用错位相减法
2*T(h)= 2^1*(h-1)+2^2*(h-2)+2^3*(h-3)+2^4*(h-4)+...+2^(h-1)*1 (2)
(2)-(1)得
T(n)= 2^1+2^2+2^3+...+2^(h-2)+2^(h-1)-(h-1) =2^0+ 2^1+2^2+2^3+...+2^(h-2)+2^(h-1)-h
再有等比数列求和可得
T(h) = 2^h - 1 - h 又由于
我们可以将函数转为节点为自变量的函数
T(n) = n -
由大O表示法,我们可以得到结论
向下调整建堆算法的时间复杂度为O(N)
向上调整建堆算法的时间复杂度

我们假设树的高度为h,节点数量为N
由图中我们的分析可知
T(h) = 2^1*1+2^2*2+2^3*3+...+2^(h-2)*(h-2)+2^(h-1)*(h-1) (3)
由错位相减法可得
2*T(h) = 2^2*1+2^3*2+2^4*3+...+2^(h-1)*(h-2)+2^(h)*(h-1) (4)
由(4)-(3)得
T(h) = -(2^1+2^2+2^3+...+2^(h-1))+2^(h)*(h-1)
T(h) = -(2^0+2^1+2^2+2^3+...+2^(h-1))+2^(h)*(h-1)+2^0
T(h) = -(2^h-1)+2^h*(h-1)+ 1
又由于 ,得
T(N) = -N + (N-1)*
即向上调整建堆的时间复杂度为O(N*logN)
小结(向上调整和向下调整的差异本质)
由上面的讨论我们可以得到向下调整建堆算法的时间复杂度为O(N),向上调整建堆的时间复杂度为O(N*logN),很显然向下调整建堆算法比向上建堆算法的效率高了很多,那是为什么呢?
我们再来看一下这两个结构图
向下调整

向上调整

我们可以发现,向下调整建堆是
- 节点数量多的层*调整次数少
- 节点数量少的层*调整次数多
而向上调整建堆则是
- 节点数量多的层*调整次数多
- 节点数量少的层*调整次数少
这就是向上调整和向下调整算法时间复杂度差别很大的区别本质
堆中的TOPK问题
所谓TopK问题,即在N个数中找到最大的K个数,假设N远远大于K
方法1:
建立大堆 时间复杂度为O(N)
popk次,便找到了最大的k个数 时间复杂度为O(klogN)
这个方法可行,但是有一个非常明显的弊端,因为堆是放在数组里存储的,能够进行随机访问的,假设我们的N为是十亿个整数,那么就意味着我们要建堆的空间为十亿*sizeof(int)个字节,那么大概率是无法开辟的,即便开辟效率也太低了。
那么我们有一个方法,我们可以依次建多个堆,将数据分开,假设K=10,我们将N分为M份。则每个堆的数据一共就有N/M个,然后我们取每个堆的最大的10个数,记录这10个数,销毁堆,再找到下面堆的10个数,最后将10*m个数再放到一块进行比较,找出最大的10个数。
虽然这个方法可以大大减少内存的使用,但还是有些浪费空间
方法2(重点):
用前K个数建一个小堆
然后再让N-K个数依次和堆顶进行比较,如果大于堆顶的数就交换堆顶的数据,再向下调整,最后这小堆中的数据就是原数据中最大的k个数据
时间复杂度为(logk*(N-K))
根据大O时间复杂度为O(N)
而且空间只需要sizeof(int)*k 效率大大提升,这个方法特别优秀,下面我们将引一个例子,用代码来具体解释这个算法。
1.创建数据
我们将创建10万个数据,寻找其最大的前K个数
我们用srand来创建随机数,将其写入到文件里
这里需要用 C语言文件的读写 的知识
由于仅仅用rand创建随机数会有很多重复的数据,因此我们令x = rand()+i 这样可以很大一部分筛出重复的数据
void createData()
{
int n = 100000;
srand(time(0));
const char* file = "data.txt";
FILE* fin = fopen(file, "w");
if (fin == NULL)
{
perror("fopen fail");
return;
}
for (int i = 0; i < n; i++)
{
int x = (rand() + i) % 1000000;
fprintf(fin, "%d\n", x);
}
fclose(fin);
}文件中将会有10万个随机整数,如图所示

2.完成对topk的逻辑处理
有了数据后,我们就需要开始对这些数据按照思路二进行实现
包括向下调整建堆,交换堆顶数据等逻辑
代码实现如图所示
void TEST()
{
const char* file = "data.txt";
FILE* fout = fopen(file, "r");
if (fout == NULL)
{
perror("fopen fail");
return;
}
int k;
printf("请输入k:>");
scanf("%d", &k);
int* kminheap = (int*)malloc(sizeof(int) * k);
if (kminheap == NULL)
{
perror("malloc fail");
return;
}
for (int i = 0; i < k; i++)
{
fscanf(fout,"%d", &kminheap[i]);
}
for (int i = (k-1-1)/2; i >=0; i--)
{
AdjustDown(kminheap,k,i);
}
//读取剩下的n-k个数
int x = 0;
while (fscanf(fout, "%d", &x)>0)
{
if (x > kminheap[0])
{
kminheap[0] = x;
AdjustDown(kminheap, k, 0);
}
}
printf("最大的前%d个数", k);
for (int i = 0; i < k; i++)
{
printf("%d ", kminheap[i]);
}
printf("\n");
}效果如图所示
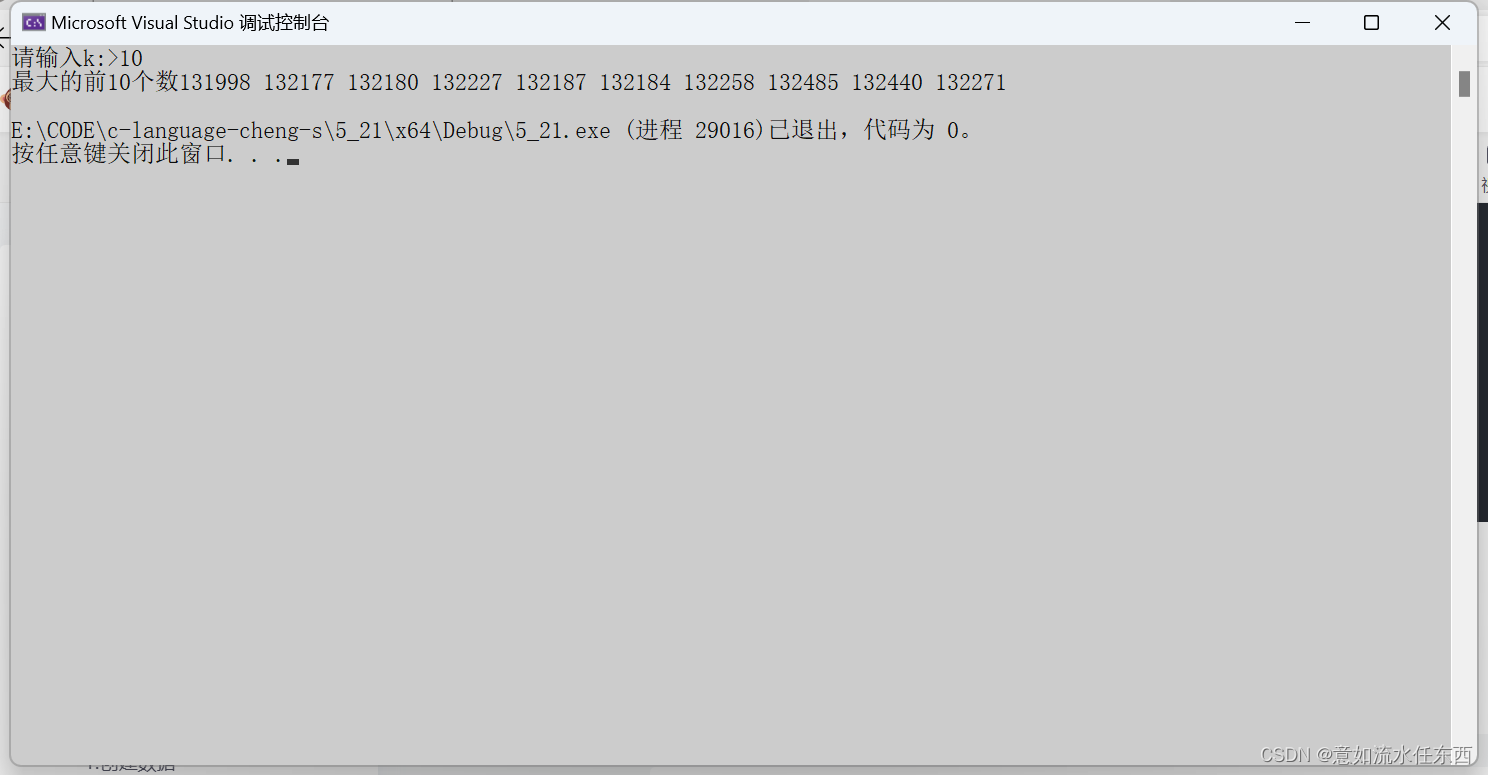
总结
本篇文章,我们推到了向下调整建堆算法和向上调整建堆的时间复杂度,还有堆的topk问题,我们从逻辑方面,用数学公式详细的介绍了算法时间复杂度,希望本篇文章能帮助到正在努力的你。
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








