二叉树复习（C语言版）

于 2025-05-14 13:34:04 发布
阅读量699 收藏 13
点赞数 16
文章标签： c语言 数据结构 二叉树
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/2302_80297338/article/details/147457797
版权

目录

1.前中后序遍历介绍

2.前中后序遍历代码实现

3.结点个数、结点查询与二叉树的销毁代码实现

4.层序遍历、完全二叉树的判断

5.递归使用时的常见错误：

6.二叉树和堆相关考试题

7.总结

1.前中后序遍历介绍

前序：根 左子树 右子树（先访问根结点，再访问左子树，再访问右子树）

中序：左子树 根 右子树（先访问左子树，再访问根节点，再访问右子树）

后序：左子树 右子树 根（先访问左子树，再访问右子树，再访问根节点）

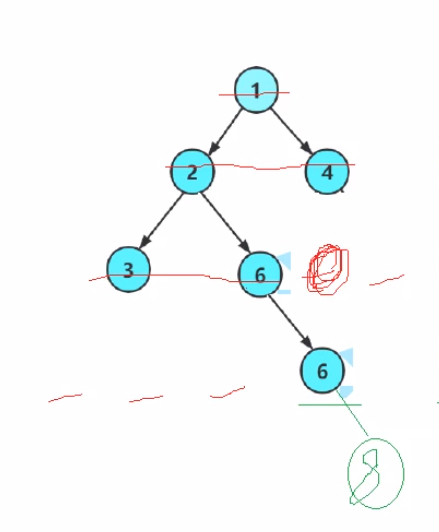
需要进行遍历的二叉树如上图所示。

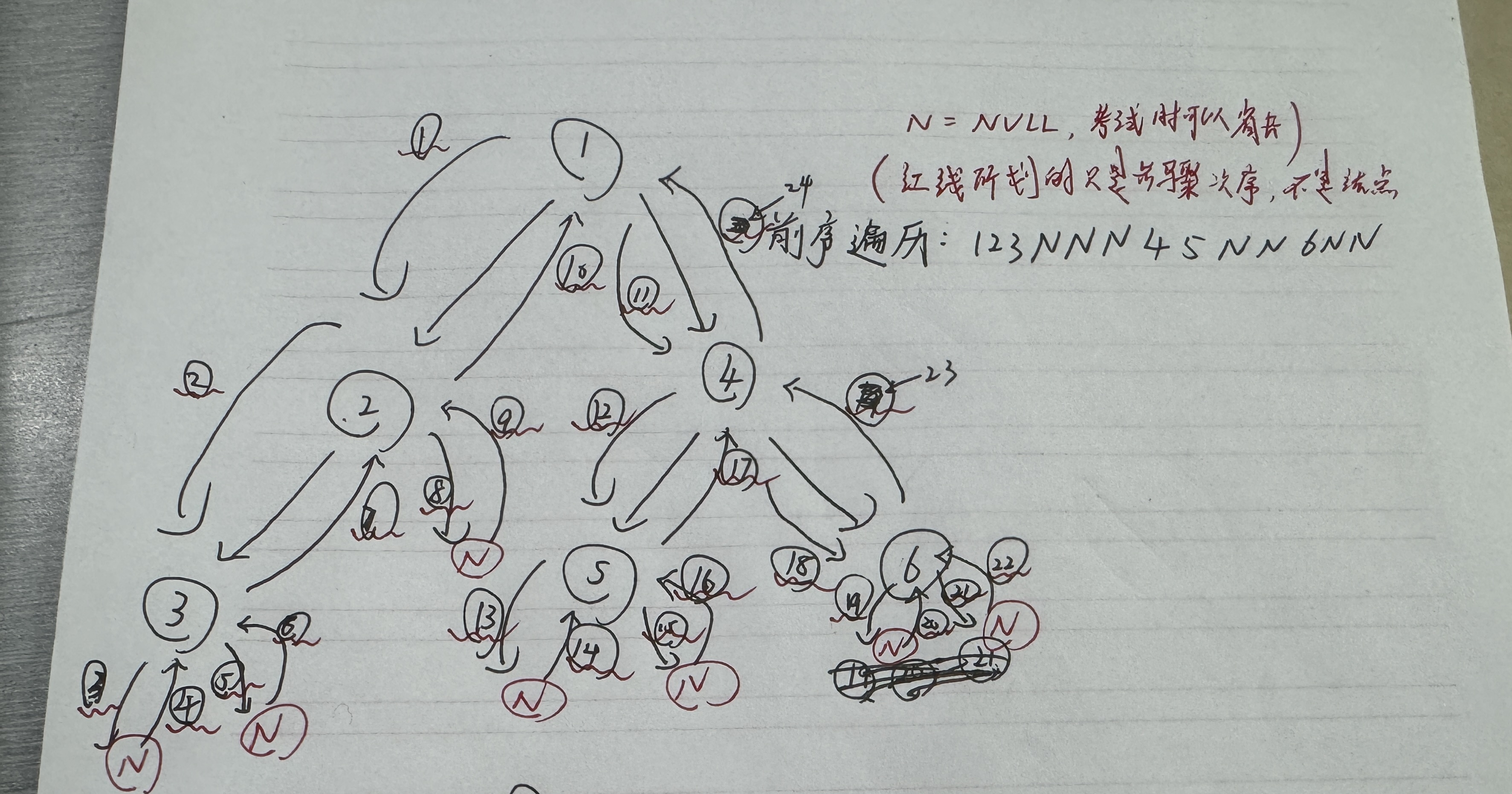
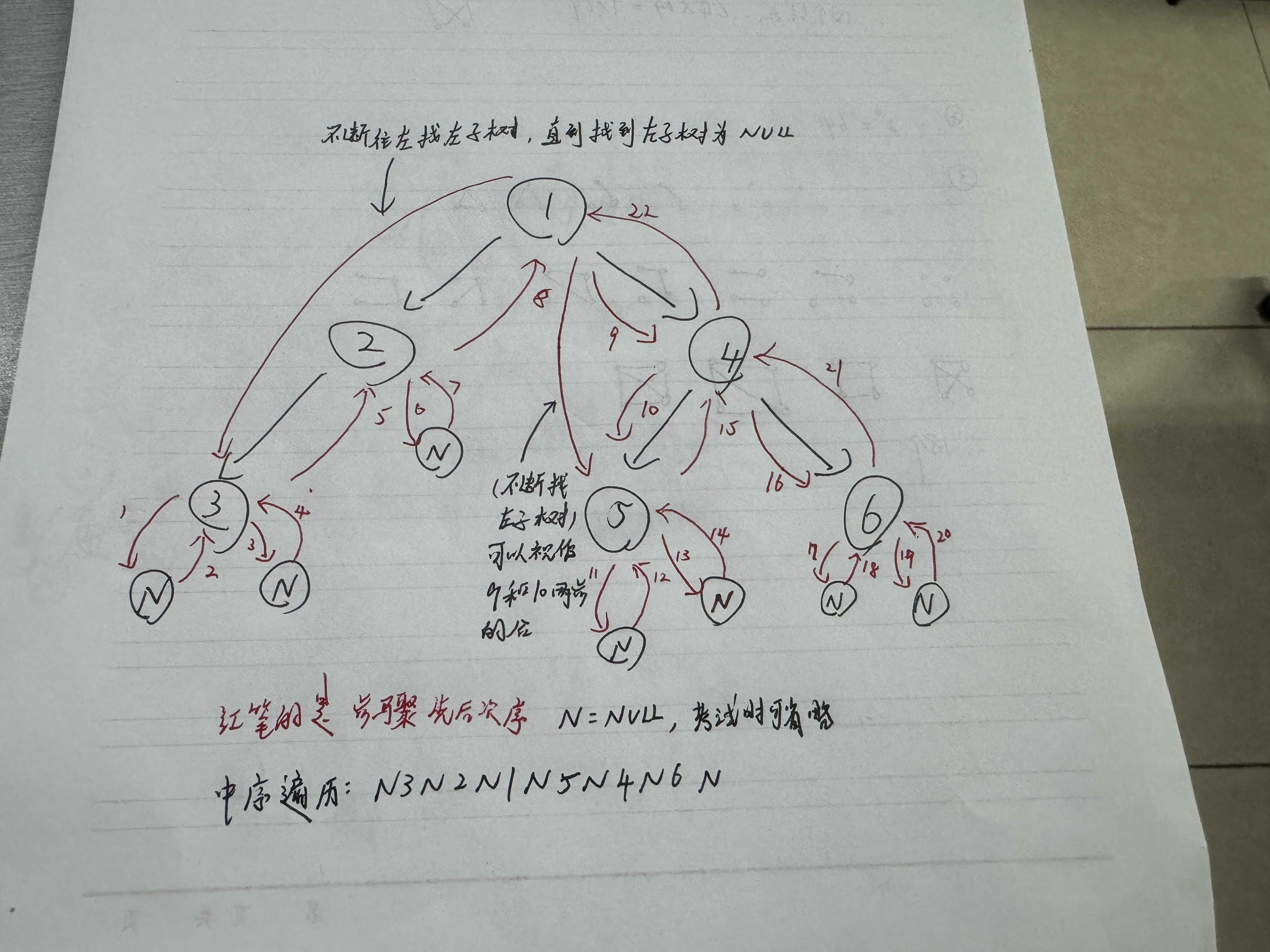
前序遍历就是把一整棵树看成是根节点+左子树+右子树，然后再把左子树的根节点看作是根节点+左子树+右子树（这也是为什么用递归来解决三种二叉树遍历），直到左右子树都为NULL时，往上返回。中序遍历、后序遍历就是访问的顺序更改了，依旧是有异曲同工之妙的。

前序遍历的结果为123456，中序遍历的结果为321546，后序遍历的结果为325641（前序、中序流程图下面已给，后序遍历流程图略）

层序遍历：一层一层遍历

还是以上图所示的二叉树为例，结果为124356

2.前中后序遍历代码实现

#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
#include<assert.h>

typedef int TreeData;

typedef struct TreeNode
{
	TreeData val;

	struct TreeNode* left;
	struct TreeNode* right;  
}Tnode;


Tnode* buynode(int x)
{
	Tnode* newnode = (Tnode*)malloc(sizeof(Tnode));
	if (!newnode)
	{
		perror("malloc failure");
		return;
	}

	newnode->val = x;
	newnode->left = newnode->right = NULL;
	return newnode;
}

Tnode* CreateTree()//初始化一个二叉树，来对其增删改查（此处初始化的二叉树为上图给的那一棵）
{
	Tnode* node1 = buynode(1);
	Tnode* node2 = buynode(2);
	Tnode* node3 = buynode(3);
	Tnode* node4 = buynode(4);
	Tnode* node5 = buynode(5);
	Tnode* node6 = buynode(6);

	node1->left = node2;
	node1->right = node4;
	node2->left = node3;
	node4->left = node5;
	node4->right = node6;

	return node1;//返回整个二叉树的根节点
}

void PrevOrder(Tnode* cur)
{
	if (!cur)
	{
		printf("N ");
		return;
	}

	printf("%d ", cur->val);
	PrevOrder(cur->left);
	PrevOrder(cur->right);
}


int main()
{
	Tnode* rootnode = CreateTree();
	PrevOrder(rootnode);
	return 0;
}

在二叉树的遍历当中，递归的作用就是先在左子树不断往左找，找到NULL返回，然后再往右找，找到NULL返回；随后在右子树重复这一操作，并根据不同的遍历访问顺序，进行细微的调整；例如前序遍历每次先打印根节点，然后再不断往左找往右找；由于同一种遍历时用到的访问顺序是相同的，所以需要调用的函数代码也是相同的，因此可以用到递归来去实现

void MidOrder(Tnode* cur)//中序
{
	if (!cur)
	{
		printf("N ");
		return;
	}

	MidOrder(cur->left);
	printf("%d ", cur->val);
	MidOrder(cur->right);
}

void LastOrder(Tnode* cur)//后序
{
	if (!cur)
	{
		printf("N ");
		return;
	}

	LastOrder(cur->left);
	LastOrder(cur->right);
	printf("%d ", cur->val);
}

 因为对二叉树的遍历而言，函数的栈帧可以共用（因为二叉树的遍历是递与归交替执行的，所以使用了一些栈帧以后，又返回了一些栈帧，因而被返回的栈帧又可以共用给后续需要调用的函数）

对于一棵高度为3的二叉树来说，只需要开辟4个栈帧就可以完成操作，不会有栈溢出的风险；而高度为3的二叉树最多能存放 2^4 - 1 = 15 个结点，因此对于大量数据的递归调用，二叉树这一数据结构可以让栈溢出风险降至最低

3.结点个数、结点查询与二叉树的销毁代码实现

Tnode* buynode(int x)
{
	Tnode* newnode = (Tnode*)malloc(sizeof(Tnode));
	if (!newnode)
	{
		perror("malloc failure");
		return;
	}

	newnode->val = x;
	newnode->left = newnode->right = NULL;
	return newnode;
}

Tnode* CreateTree()//初始化一个二叉树，来对其增删改查（此处初始化的二叉树为上图给的那一棵）
{
	Tnode* node1 = buynode(1);
	Tnode* node2 = buynode(2);
	Tnode* node3 = buynode(3);
	Tnode* node4 = buynode(4);
	Tnode* node5 = buynode(5);
	Tnode* node6 = buynode(6);

	node1->left = node2;
	node1->right = node4;
	node2->left = node3;
	node4->left = node5;
	node4->right = node6;

	return node1;//返回整个二叉树的根节点
}

int TreeSize(Tnode* cur)//求结点个数优化版
{
	return cur == NULL ? 0 : TreeSize(cur->left) + TreeSize(cur->right) + 1;
}

int TreeLeafSize(Tnode* cur)//求叶结点的个数
{
	if (!cur)//为空时不能进行解引用判断左右子树
		return 0;
	if (cur->left == NULL && cur->right == NULL)//左右皆空即为叶子结点
		return 1;
	return TreeLeafSize(cur->left) + TreeLeafSize(cur->right);
}

int TreeHeight(Tnode* cur)//求树的高度
{
	if (!cur)
		return 0;
	//return TreeHeight(cur->left) > TreeHeight(cur->right) ? TreeHeight(cur->left) + 1 : TreeHeight(cur->right) + 1;
	int leftheight = TreeHeight(cur->left);
	int rightheight = TreeHeight(cur->right);
	return leftheight > rightheight ? leftheight + 1 : rightheight + 1;
	
}

int TreeLevelKSize(Tnode* cur,int k)
{
	if (!cur) return 0;
	if (k == 1) return 1;
	return TreeLevelKSize(cur->left, k - 1) + TreeLevelKSize(cur->right, k - 1);//每次都往下一层
}

Tnode* TreeFind(Tnode* cur, int x)
{
	if (cur == NULL) return NULL;
	if (cur->val == x)return cur;

	//下面代码是为了防止到了cur，既不是空，结点值也不是x时，这种时候没有返回值
	Tnode* temp1 = TreeFind(cur->left, x);
	if (temp1) return temp1;
	Tnode* temp2 = TreeFind(cur->right, x);
	if (temp2) return temp2;
	return NULL;
}

void TreeDestory(Tnode* cur)
{
	if (cur == NULL) return;

	TreeDestory(cur->left);
	TreeDestory(cur->right);
	free(cur);
}

int main()
{
	Tnode* rootnode = CreateTree();
	printf("TreeSize：%d\n",TreeSize(rootnode));
	printf("TreeSize：%d\n", TreeSize(rootnode));
	printf("TreeSize：%d\n", TreeSize(rootnode));
	printf("TreeLeafSize：%d\n", TreeLeafSize(rootnode));
	printf("TreeHeight：%d\n", TreeHeight(rootnode));
	printf("TreeLevelKSize：%d\n", TreeLevelKSize(rootnode, 2));
	printf("TreeLevelKSize：%d\n", TreeLevelKSize(rootnode, 3));
	Tnode* ret = TreeFind(rootnode,5);
	printf("%d", ret->val);
    TreeDestory(rootnode);
	return 0;
}

TreeSize函数：
1.空 ，0个
2.非空 ， 左子树结点个数 + 右子树结点个数 + 1

通过这个例子我们不难发现，递归算法题目是把一整个问题拆分成子问题的集合，然后就考虑其中一个子问题的解决方法，这个解决方法可以解决所有子问题（因为子问题的解决方法相同），这样就可以把一整个问题解决掉了

TreeHeight函数：

1.空 为0
2.非空 左子树高度、右子树高度大的那个 + 1

TreeLevelKSize函数：

子问题为求出第i层某一个根节点左右子树（i+1层）所有符合条件的结点数量（逆向思考即从k到k-1）

为空时不管在哪层，直接返回0；不为空且k为1时说明到了求的那层（下文有图片演示）

TreeDestory函数：

对于一整棵树来说，先删除左子树，再删除右子树，最后再删除根结点，这样才会找得到要删除的左子树、右子树 -> 后序遍历删除

4.层序遍历、完全二叉树的判断

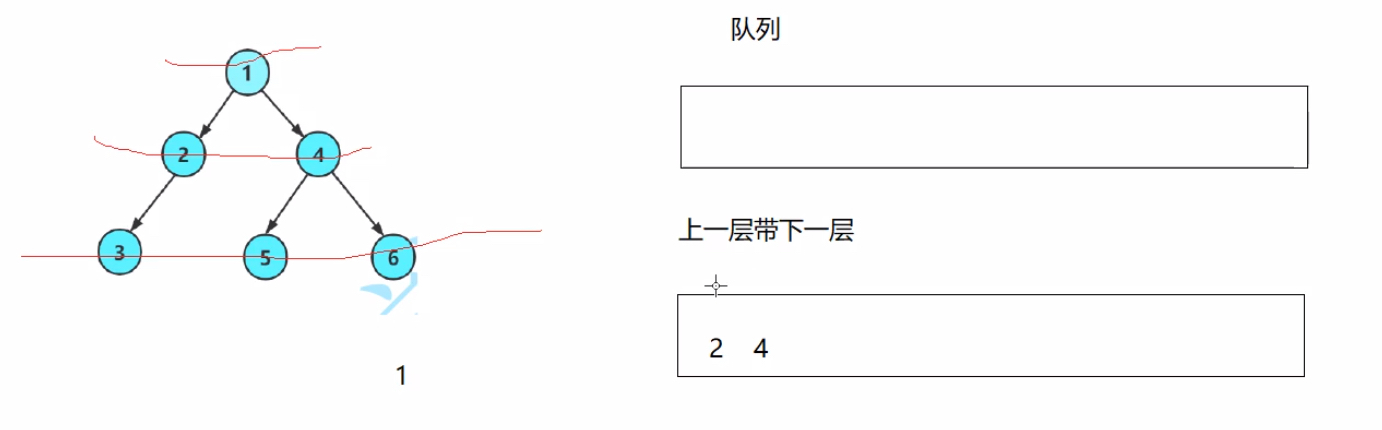
前中后序遍历是深度优先遍历（DFS)、层序遍历是广度优先遍历(BFS)

通过队列来完成，进入根节点（val == 1）之后，再出根节点，把根节点相连接的2个下层结点放进队列；然后再出一个结点（val == 2），然后把该结点相连的下层结点再放进对列把结点作为元素，放入拿出队列……（以此类推，即可完成层序遍历）

大致流程如上图所示

typedef struct QueueNode{
    struct QueueNode* next;
    QDataType val;
}QNode;

typedef struct Queue{
    QNode* ptail;
    QNode* phead;
    int size; 
}Queue;

typedef Struct TreeNode* QDataType;

void QueueInit(Queue* q)
{
    assert(q);
    q->phead = NULL;
    q->ptail = NULL;
    q->size = 0;
}

void QueuePush(Queue* q,QDataType x)
{
    QNode* newnode = (QNode*)malloc(sizeof(QNode));
    if(newnode == NULL)
    {
        perror("malloc error");
        return ;
    }

    newnode->next = NULL;
    newnode->val = x;
    if(q->ptail == NULL)
        q->phead = q->ptail = newnode;
    else
    {
        q->ptail->next = newnode;
        q->ptail = newnode;
    }
    q->size++;

}


void QueuePop(Queue* q)
{
    assert(q);
    assert(q->size!=0);

    if(q->phead->next==NULL)
    {
        free(q->phead);
        q->phead = q->ptail = NULL;
    }
    else
    {
        QNode* next = q->phead->next;
        free(q->phead);
        q->phead = next;
    }
   q->size--;
}

int QueueSize(Queue* q)
{
    assert(q);
    return q->size;
}


QDataType QueueFront(Queue* q)
{
    assert(q);
    return q->phead->val;
}

QDataType QueueBack(Queue* q)
{
    assert(q);
    return q->ptail->val;
}

void TreeLevelOrder(Tnode* cur) //前中后序遍历是深度优先遍历（DFS)、层序遍历是广度优先遍历(BFS)
{
	Queue q;
	QueueInit(&q);//初始化函数
	if (cur)
		QueuePush(&q, cur);//插入队列
	while (QueueSize(&q) != 0)
	{
		Tnode* front = QueueFront(&q);//获取队头元素
		QueuePop(&q);//删除队头元素

		printf("%d ", front->val);
		if (front->left) QueuePush(&q, front->left);
		if (front->right)QueuePush(&q, front->right);

	}
}
//……

怎么用代码判断一棵树是否为完全二叉树？

解决办法：
1.层序遍历，NULL也入队列
2.遇到第一个空结点时，后面全空就是完全二叉树，有非空就不是完全二叉树
后面指的是当前空结点同层的后面，或者该空结点的下一层；因为层序遍历一层一层往下，所以到该结点时，所有的非空结点肯定都进入队列了（后面的非空结点肯定是前面非空结点的孩子）；如果该结点的下下层还有，是否进入队列已经不会影响结果了

下面2张图是图文解释

//……
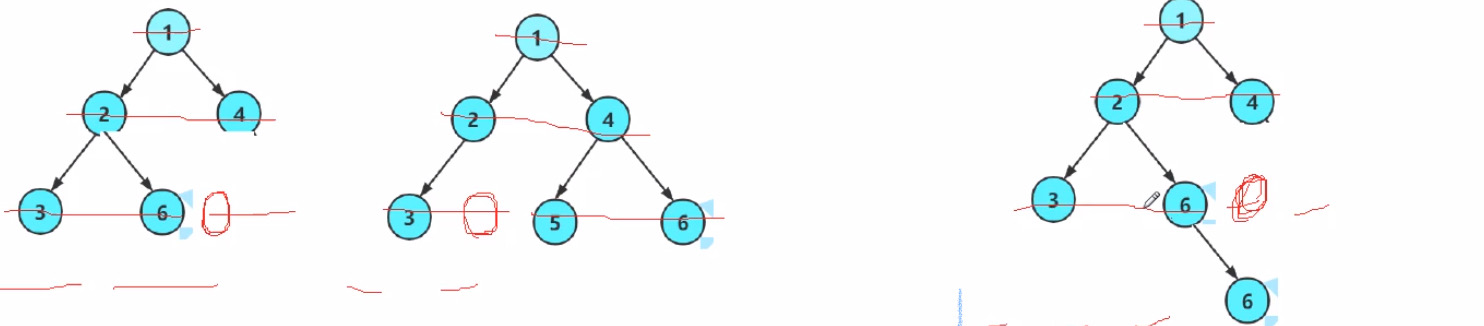
bool CompleteBinTree(Tnode* cur)//判断一棵树是否为完全二叉树
{
	Queue q;
	QueueInit(&q);
	if (cur)
		QueuePush(&q, cur);
	while (QueueSize(&q) != 0)
	{
		Tnode* front = QueueFront(&q);
		QueuePop(&q);

		if (front == NULL)
			break;
		QueuePush(&q, front->left);
		QueuePush(&q, front->right);
	}
	while (QueueSize(&q) != 0)
	{
		Tnode* front = QueueFront(&q);
		QueuePop(&q);
		if (front) return false;
	}
	return true;
	printf("\n");
}
//……

5.递归使用时的常见错误：

1.递归调用的函数中创建的变量每次都被初始化，如果使用static解决则结果每次都被保留

解决办法：全局变量+使用函数前修改 || 修改代码逻辑

int TreeSize(Tnode* cur)//求结点个数
{
	//static size = 0; 
	//用一个静态的size，让其只初始化一次；但这会导致只有第一次调用函数，能够得到正确答案，之后再调用该函数会得到6的倍数结果；所以我们应该改成使用全局变量，让其能够被修改的同时，不会被多次初始化
	if (!cur) return size;

	size++;
	TreeSize(cur->left);
	TreeSize(cur->right);
	return size;
}

2. 求树的高度时前后2种方式性能的差异：
    对于第1种，假设到了数值为6的最后一个结点（假设为a），在判断时先需要调用左右两子树的高度函数，判断为假然后进入到 TreeHeight(cur->right) + 1，此时第二次调用该结点右子树（假设为b）的高度函数
    然后返回到了数值为3的结点，返回以后先调用左右两子树的高度函数，判断为假又调用了该结点右子树（a）的高度函数；进入到右子树（a）高度函数后，又需要判断左右两子树的高度，判断为假后第四次调用结点右子树（b）的高度函数
    周而复始，会不断地重复调用已经计算过的函数；高度越高，重复调用的情况就越严重；比如高度为10的树，最坏情况下某空结点要调用函数判断20次（2*10 = 20，该空结点一直作为较高子树的最末尾）
    因此第一种方式过于冗余，在性能上较差
    对于第2种，递归调用了以后，用了一个变量保存了下来；那么在判断完大小关系以后，可以直接返回变量 + 1的结果，不需要再次调用函数
    同时，因为函数把下层的子树高度返回值用变量保存了下来，因此在判断时可以直接使用了，无需再次调用函数获得子树高度返回值
    因此第2种方式性能较好，推荐使用第2种（下文有图片演示）

解决方法：在递归函数中，尽量不要出现同一参数的多次函数调用（例如代码1就是cur->left或cur->right会放进函数调用2次）

int TreeHeight(Tnode* cur)//求树的高度
{
	//1.空 为0
	//2.非空 左子树高度、右子树高度大的那个 + 1
	if (!cur)
		return 0;
	return TreeHeight(cur->left) > TreeHeight(cur->right) ? TreeHeight(cur->left) + 1 : TreeHeight(cur->right) + 1;
}
//代码1
int TreeHeight(Tnode* cur)//求树的高度
{
	//1.空 为0
	//2.非空 左子树高度、右子树高度大的那个 + 1
	if (!cur)
		return 0;
	int leftheight = TreeHeight(cur->left);
	int rightheight = TreeHeight(cur->right);
	return leftheight > rightheight ? leftheight + 1 : rightheight + 1;
}

 

3.到了cur，既不是空，结点值也不是x时，这种时候没有返回值，即递归过程中没有返回值

解决方法：上文已给出，人为返回NULL或具体节点

Tnode* TreeFind(Tnode* cur, int x)
{
	if (cur == NULL) return NULL;
	if (cur->val == x)return cur;

	TreeFind(cur->left, x);
	TreeFind(cur->right, x);
}

4.函数传参以后，形参因为返回后没有被修改，导致递归结果和所需结果不同

解决方法：传参时传形参地址（代码示例：leetcode二叉树相关题目复习）

6.二叉树和堆相关考试题

1. 某二叉树共有 399 个结点，其中有 199 个度为 2 的结点，则该二叉树中的叶子结点数为（ ）
A 不存在这样的二叉树
B 200
C 198
D 199
度为2的分支结点个数 = 度为0的叶节点个数 - 1；所以结果为 B
2.下列数据结构中，不适合采用顺序存储结构的是（ ）
A 非完全二叉树
B 堆
C 队列
D 栈
堆使用的完全二叉树思想，所以可以采用；栈用顺序结构能够满足FIFO（先进先出），所以可以采用；队列不太适合，但因为可以使用顺序存储结构来实现循环队列，因此要比非完全二叉树采用顺序存储结构好；所以如果是 单选就选A， 多选选AC
3.在具有 2n 个结点的完全二叉树中，叶子结点个数为（ ）
A n
B n+1
C n-1
D n/2
假设：
度为0的结点个数：a；度为1的结点个数：b；度为2的结点个数：c
a + b + c  = 2n
又 a = c + 1（概念）
所以 a + b + a - 1 = 2n
完全二叉树 b = 1 or 0（完全二叉树的性质，对于完全二叉树来说，至多只可以有一个结点有一个左节点）
若 b = 1，2a = 2n，a = n；若 b = 0，2a = 2n + 1，无法除尽所以舍去（说明具有2n个结点的完全二叉树必须有一个度为1的结点，假如是一棵具有2n+1个结点的完全二叉树，也可以通过是否可以除尽来判断结果）
所以结果为 A
真正考试时，如果是选择题，可以画一个只有2个结点的完全二叉树，然后 2n = 2，叶子结点为1，n = 1，所以直接选A
4.一棵完全二叉树的结点数位为531个，那么这棵树的高度为（ ）
A 11
B 10
C 8
D 12
高度 = log2(531+1)
9 < log2(531+1) < 10 ，所以结果为 B
5.一个具有767个结点的完全二叉树，其叶子结点个数为（ ）
A 383
B 384
C 385
D 386
做法同题3，结点数看作767 = 2n+1，最后结果为n + 1，即最后结果为 B
6.下列关键字序列为堆的是：（）
A 100,60,70,50,32,65
B 60,70,65,50,32,100
C 65,100,70,32,50,60
D 70,65,100,32,50,60
E 32,50,100,70,65,60
F 50,100,70,65,60,32
把选项抽象成完全二叉树，判断上下两层的大小关系(也可以用完全二叉树子节点、父节点的下标关系来挑出要判断的2个数，推荐抽象成完全二叉树，因为比较简单方便），单调递减or递增就是堆
100 > 60 and 70
60 > 50 and 32
70 > 65
所以结果为 A
7.已知小根堆为8,15,10,21,34,16,12，删除关键字 8 之后需重建堆，在此过程中，关键字之间的比较次数是（）。
A 1
B 2
C 3
D 4
如果要将8删除，先是12、8互换位置，然后12开始进行向下调整
10 < 12 < 15，10 和 12 互换位置 （第一次+第二次，和15、10比较两次）
12 < 16，不互换位置（第三次）
所以结果为 C        
8.一组记录排序码为(5 11 7 2 3 17),则利用堆排序方法建立的初始堆为
A(11 5 7 2 3 17)
B(11 5 7 2 17 3)
C(17 11 7 2 3 5)
D(17 11 7 5 3 2)
E(17 7 11 3 5 2) 
F(17 7 11 3 2 5)
对于一个数组（排序码）来说，从最后一个父节点开始，依次向下调整，直到调整到根节点为止 
5 11 17 2 3 7 -> 5 11 17 2 3 7 -> 17 11 5 2 3 7 -> 17 11 7 2 3 5
所以结果为 C
9.最小堆[0,3,2,5,7,4,6,8],在删除堆顶元素0之后，其结果是（）
A[3，2，5，7，4，6，8]
B[2，3，5，7，4，6，8]
C[2，3，4，5，7，8，6]
D[2，3，4，5，6，7，8]
思路同题7
8 3 2 5 7 4 6 -> 2 3 8 5 7 4 6 -> 2 3 4 5 7 8 6
所以结果为 C
10.某完全二叉树按层次输出（同一层从左到右）的序列为 ABCDEFGH 。该完全二叉树的前序序列为（
）
A ABDHECFG
B ABCDEFGH
C HDBEAFCG
D HDEBFGCA
根左右的遍历顺序，不难得出结果为 A（可以借助画图）
11.二叉树的先序遍历和中序遍历如下：先序遍历：EFHIGJK;中序遍历：HFIEJKG.则二叉树根结点为（）
A E
B F
C G
D H
前序遍历的第一访问结点即整棵树的根节点，所以结果为 A
12.设一课二叉树的中序遍历序列：badce，后序遍历序列：bdeca，则二叉树前序遍历序列为____。
A adbce
B decab
C debac
D abcde
后序遍历（左右根）最后访问整棵树的根节点，因此前序遍历第一个访问的是a，B、C排除
中序遍历（左根右），根节点a的左边访问了b，因此根节点的左子树只有一个结点b
前序遍历（根左右）不难得出结果为 D
13.某二叉树的后序遍历序列与中序遍历序列相同，均为 ABCDEF ，则按层次输出（同一层从左到右）的序列为（）
A FEDCBA
B CBAFED
C DEFCBA
D ABCDEF
根为F，因此结果为 A

7.总结

递归调用时，可以把递归调用的函数看作是树的子树， root->left 即左子树 ，root->right 即右子树

整个二叉树就可以拆分成多个这样的子树，由子树的子树组成了子树，再由子树组成了二叉树

评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值