婚姻匹配问题

问题描述

有N男N女，每个人都按照他对异性的喜欢程度排名。现在需要写出一个算法安排这N个男的、N个女的结婚，要求两个人的婚姻应该是稳定的。何为稳定?有两对夫妻M1 F2，M2 F1.M1心目中更喜欢F1，但是他和F2结婚了，M2心目中更喜欢F2，但是命运却让他和F1结婚了，显然这样的婚姻是不稳定的，随时都可能发生M1和F1私奔或者M2和F2私奔的情况。所以在做出匹配选择的时候（也就是结婚的时候），我们需要做出稳定的选择，以防这种情况的发生。

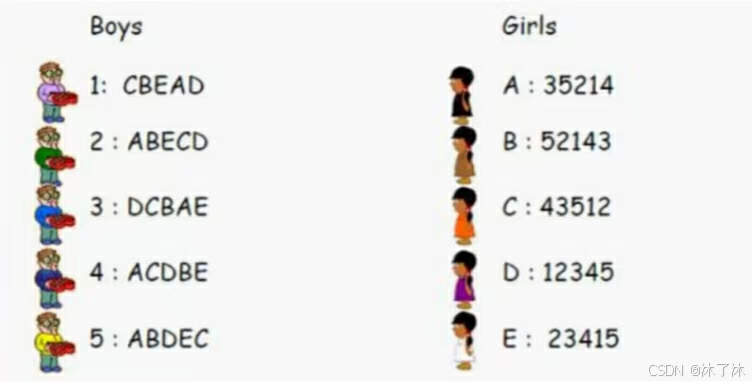
要求：boys 和girls 各自给出自己心仪的嘉宾的顺序，请编写程序求出一种稳定的匹配，使匹配结果不会发生私奔现象。

算法设计

Gale-Shapley算法是一种用于解决稳定婚姻问题的高效算法，它总是能找到稳定的匹配。该算法的核心思想是每个未匹配的男性向他最喜欢的女性求婚，如果这位女性还未被匹配，则接受他的求婚；如果她已经被匹配，但更喜欢这个新的求婚者，她会拒绝当前的配偶并与新求婚者匹配。这个过程一直重复，直到所有人都被匹配。

设计思路：

①初始化：所有男性和女性都未被匹配。

②迭代过程：对于每个未匹配的男性，他向列表中的第一个（最喜欢的）未被匹配的女性求婚。如果女性已经匹配，比较她当前的配偶和新求婚者，如果她更喜欢新求婚者，则与新求婚者匹配。否则，保持当前匹配。

③终止条件：当所有人都被匹配时，算法结束。

运行代码：

#include <stdio.h> 
#include <iostream>
using namespace std;
// 函数声明，将数字转换为大写字母
char numToUpperChar(int num1);
// 函数声明：检查是否所有男孩都完成了配对
bool finish(int, int *);
// 函数声明：判断女孩是否更喜欢追求者而不是当前对象
bool boysPrefer(int num, int *girls, int date, int chasing);
int main(){
    printf("婚姻匹配问题\n"); // 输出标题信息
    int num; // 存储需要配对的对数
    int i,j; // 循环变量
    printf("请输入需要配对的对数："); // 提示用户输入配对数量
    scanf("%d",&num); // 读取用户输入的配对数量
    int boys[num][num]; // 存储每个男孩心中的女孩排名
    int girls[num][num]; // 存储每个女孩心中的男孩排名
    // 获取每个男孩心中的女孩排名
    for (int i = 0; i < num; i++){
        printf("男孩%d心中的女孩排行：",i+1); 
        for (int j = 0; j < num; j++){
            scanf("%d",&boys[i][j]);
        }
    }
    // 获取每个女孩心中的男孩排名
    for (int i = 0; i < num; i++){
        printf("女孩%d心中的男孩排行：",i+1); 
        for (int j = 0; j < num; j++){
            scanf("%d",&girls[i][j]);
        }
    }
   //男孩和女孩目前已配对的对象
    int *boy = new int[num]; // 动态分配数组，存储男孩的配对状态
    int *girl = new int[num]; // 动态分配数组，存储女孩的配对状态
    for (int i = 0; i < num; i++){
        boy[i] = 0; // 初始化男孩配对状态为未配对
        girl[i] = 0; // 初始化女孩配对状态为未配对
    }
    //男孩追求过的女孩的数量
    int *numboy = new int[num]; // 动态分配数组，记录男孩的追求次数
    for (int i = 0; i < num; i++){
        numboy[i] = 0; // 初始化男孩追求次数为0
    }
    // 开始配对过程
    do{
        for (int i = 0; i < num; i++){
            printf("检查男孩%d是否有对象\n",i+1);//按序号遍历所有男孩
            if (boy[i] == 0){//如果某男孩没有对象
                printf("男孩%d没有对象,可以追求女孩！\n",i+1); 
                //该男孩准备追求优先表中还没追求过的排名最高的女孩
                int boychase = girls[i][numboy[i]];//男孩追求的女孩
                int dateboychase = girl[boychase - 1];//判断该男孩准备追求的女孩现在是否单身
                printf("男孩%d准备追女孩%d！\n",i+1,boychase);
                if (dateboychase != 0){
                    printf("女孩的对象是%d！\n", dateboychase); // 输出女孩当前的对象
                } else {
                    printf("女孩%d现在是单身！\n",boychase); // 输出女孩目前单身的信息
                }
                
                if (dateboychase == 0){//如果该男孩准备追求的女孩单身
                    boy[i] = boychase;//该男孩的对象变成准备追求的女孩
                    girl[boychase - 1] = i + 1;//女孩的对象变成该男孩
                    printf("男孩%d和女孩%d在一起了！\n",i+1,boychase); // 输出配对成功信息
                } 
                //如果该男孩准备追求的女孩有对象，且她的对象在优先表中的顺序比该男孩更高，则什么都不做
				else if (boysPrefer(num, girls[boychase - 1], dateboychase, i + 1)){
                    printf("男孩%d被女孩%d拒绝了!\n" ,i+1,boychase);
                } 
                //如果该男孩准备追求的女孩有对象，且该男孩在优先表中的顺序比她的对象更高
				else {
                    boy[dateboychase - 1] = 0;//她的对象到单身状态
                    boy[i] = boychase;//该男孩的对象变成准备追求的女孩 
                    girl[boychase - 1] = i + 1;//女孩的对象变成该男孩
                    printf("男孩%d和女孩%d在一起了！\n",i+1,boychase);//输出新配对成功信息
                    printf("男生%d则恢复单身状态！\n",dateboychase);//输出原配对男孩恢复单身状态的信息
                }
                
                numboy[i]++;//增加男孩的追求次数
            } else {
                printf("男孩%d已经跟女孩%d在一起了！\n",i+1,boy[i]);//输出男孩已配对信息
            }
        }
    } while (finish(num, boy) == false); // 检查是否所有男孩都完成配对
    
    printf("\n"); 
	printf("        最终的结果                             \n"); // 输出最终结果标题
    for (int i=0; i<num;i++){
	if (boy[i] >= 0 && boy[i] <= 25) {
        char upperChar = numToUpperChar(boy[i]-1); // 调用函数转换数字为大写字母
        printf("        男孩%d - 女孩%c             \n",i+1,upperChar); // 输出每对配对结果
    	}
    }
    
    delete[] boy; // 释放动态分配的内存
    delete[] girl; // 释放动态分配的内存
    delete[] numboy; // 释放动态分配的内存
    system("pause"); // 暂停程序，等待用户操作
    return 0; // 返回程序执行状态
}

// 检查是否所有男孩都完成了配对
bool finish(int num, int *boy){
    for (int i = 0; i < num; i++){
        if (boy[i] == 0){ // 如果存在未配对的男孩
            printf("还没有完成配对\n"); // 输出未完成配对信息
            return false; // 返回false表示未完成配对
        }
    }
    printf("稳定配对完成！\n"); // 输出配对完成信息
    return true; // 返回true表示配对完成
}

// 判断女孩是否更喜欢追求者而不是当前对象
bool boysPrefer(int num, int *girls, int date, int chasing){
    int rankdate, rankchasing;//现任排行与追求者排行
    for (int i = 0; i < num; i++){
        if (girls[i] == date){ // 找到当前对象的排名
            rankdate = i+1; // 保存当前对象的排名
        }
        if (girls[i] == chasing){ // 找到追求者的排名
            rankchasing = i+1; // 保存追求者的排名
        }
    }
    printf("在女孩心目中现任排名是: %d,而追求者排名则是: %d\n",rankdate,rankchasing); // 输出排名信息
    if (rankdate < rankchasing) // 如果当前对象排名更高，返回true表示女孩更喜欢追求者
        return true;
    else // 否则返回false表示女孩更喜欢当前对象
        return false;
}
char numToUpperChar(int num1) {
    return 'A'+num1; // 利用ASCII码值进行转换
}

算法设计/问题求解中所遇到的问题及分析解决方案

数据结构的选择

问题:需要合适的数据结构来存储每个人的偏好列表和当前的匹配状态。

解决方案:

①使用数组或链表:可以使用数组或链表来存储每个人的偏好列表。对于匹配状态，可以使用布尔数组或其他数据结构来跟踪每个人是否已被匹配。

②哈希表:为了快速查找和更新匹配状态，可以使用哈希表来存储当前匹配信息。

效率问题

问题:在大型数据集上，算法的效率变得非常重要。需要考虑如何优化数据结构和算法以提高效率。

解决方案:

①剪枝策略:通过适当的剪枝策略来避免不必要的计算，从而提高算法的效率。例如，如果某个女性已经拒绝了一个男性的求婚，那么该男性可以跳过她，直接向他的下一个偏好求婚。

②并行化处理:如果可能的话，可以考虑将算法并行化处理，以提高执行速度。

边界情况处理

问题:例如，所有人的偏好都是相同的，或者某些人没有任何偏好。

解决方案:

①特殊情况处理:在算法中添加特殊情况的处理逻辑。例如，如果所有人的偏好都是相同的，可以直接返回所有人都找到他们的第一选择作为配偶的结果。如果某些人没有任何偏好，可以将这些人的匹配状态设置为单身。

②输入验证:在输入阶段进行验证，确保输入数据的有效性和一致性。

稳定性和可靠性

问题: 确保算法的稳定性和可靠性，避免因输入数据错误或算法缺陷导致的错误结果。

解决方案:

①异常处理:在算法中添加异常处理机制，捕获并处理可能出现的错误情况。

②测试覆盖:编写全面的测试用例，覆盖各种可能的情况和边界条件，确保算法的正确性和鲁棒性。

结论

婚姻匹配问题是一个经典的优化问题，它涉及到如何将一组男性与一组女性进行匹配，使得每个人都能获得最满意的配偶。这个问题可以通过多种算法来解决，其中最常用的是Gale-Shapley算法，也称为稳定婚姻算法。

在这个问题中，每个人都有一个偏好列表，表示他们愿意与之结婚的异性的顺序。目标是找到一个稳定的匹配，即没有人愿意改变自己的配偶来与其他人配对。这种匹配方式被称为“稳定婚姻”。

通过Gale-Shapley算法，我们可以有效地解决稳定婚姻问题，并找到一个稳定的匹配方案。虽然这个算法在理论上是完美的，但在实际应用中可能需要考虑更多的因素，如人们的偏好变化、文化差异等。此外，人们的偏好也可能随着时间的变化而发生变化。因此，在实际应用中，我们需要根据具体情况进行调整和优化。