b站大学系列之线代学习小结

b站大学系列之线代学习小结

写在前面

​ 这个学期我们学习了线性代数这门课程，我一直感觉学校老师讲的非常枯燥，所以在老姐的推荐下看了b站上Gilbert Strange教授的 麻省理工线代公开课，并且买了一本《Introduction to Linear Algebra》(由于是全英文的，我也只看了一部分)，不过也不能只看视频，也要多看书。如果你是还没学习过线性代数的高中生或者大学生，我非常推荐你去看一下他的视频，可以说"线代天花板"这个称号是名副其实。我写这篇文章主要是对自己第一遍看这个视频没有太搞懂的地方还有非常重要的地方再来回顾一下，这篇文章并不适合之前没有学习过线代的人观看，而且基本上都挺简略的，不一定能看懂!!!

这本书的电子版和一些习题：线性代数18.06

我在学习过程中也参考了其他人的一些笔记,也推荐一下：MIT线代笔记)还有一个公众号叫我是8位的，仅供参考。

主要内容

1.最重要的图

这张图说明了很多信息：

1.行空间和零空间都是$R^n$的子空间，列空间和左零空间都是$R^m$的子空间。

2.行空间和零空间是正交补的：①它们的交只有0，两个空间中的两个向量互相垂直；②行空间的维数是$r$,零空间的维数是$n-r$。

3.$R^n$中的任意一个向量都可以用行空间和零空间的一组基来表示。

4.对$Ax=b$的理解：①b是$A$的列向量的线性组合；②矩阵$A$将x的分量$x_r$映射映射到列空间中，将$x_n$映射成O。

2.高斯消元法解线性方程组

利用初等行变换（倍加，倍乘，对换）化为上三角矩阵。

先来看$Ax=$O的情况:

我们来分析一下，首先这种情况下肯定是有解的，而且当$r<n$(自由变量的个数为$n-r$)，如果是方阵的话$det(A)=0$（$A$的列向量是线性相关的）的情况下有非零解。然后我们再来分析一下解的结构，这一点不是很重要，但我觉得比较有意思。

我们来构造一个零空间矩阵，它的各列就是零空间的一组基，因为$A$可以最终化为$R$,我们可以通过交换列来把主列和自由列分开，即$$R=\left[\begin{array}{cc}I& F\end{array}\right]$$，然后我们可以得到零空间矩阵为$$\left[\begin{array}{c}-F\\ I\end{array}\right]$$。

【例1】：$$A=\left[\begin{array}{ccc}1& 2& 3\\ 2& 4& 6\\ 2& 6& 8\\ 2& 8& 10\end{array}\right]\text{, 求解 }\mathrm{Ax}=0\text{ 中 }\mathrm{x}\text{ 构成的零空间。 }$$

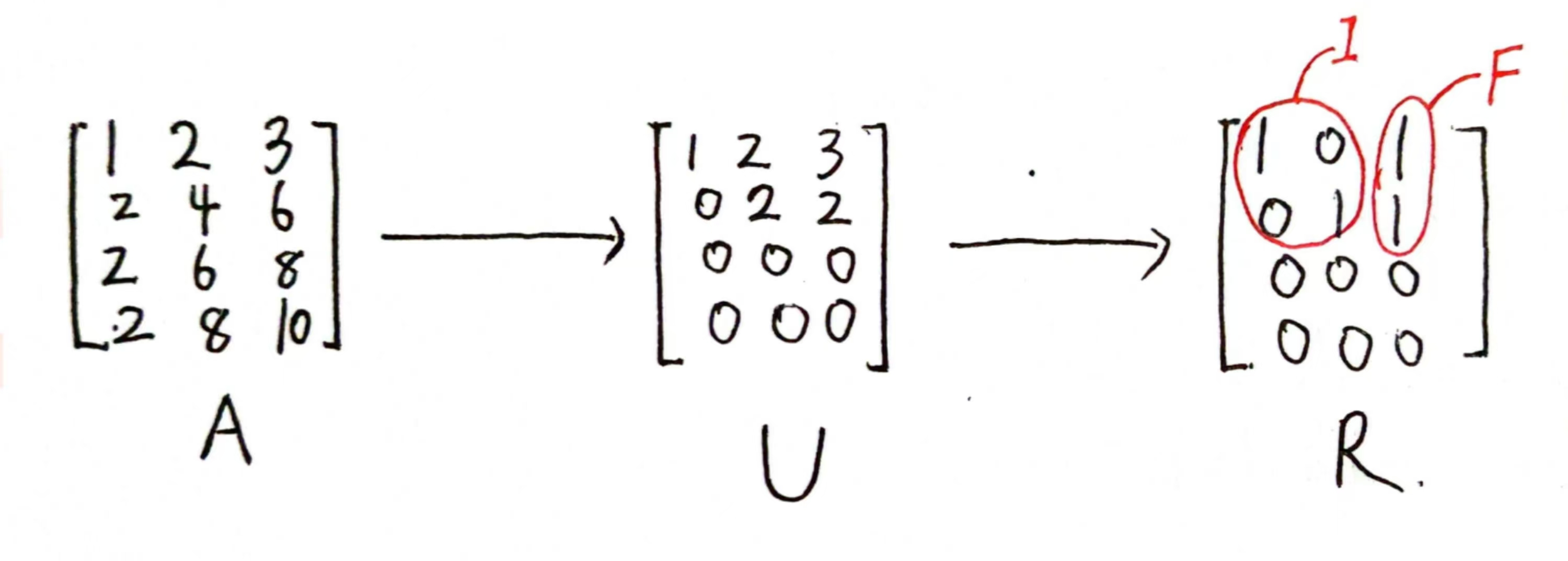
$$\therefore \mathrm{N}=\left[\begin{array}{c}-F\\ I\end{array}\right]=\left[\begin{array}{c}-1\\ -1\\ -1\\ 1\end{array}\right]$$

再来看$Ax=b$的情况：

这里我只说明一下为什么非齐次方程的通解等于齐次方程的通解加上非齐次方程的一个特殊解，从几何上很好理解：

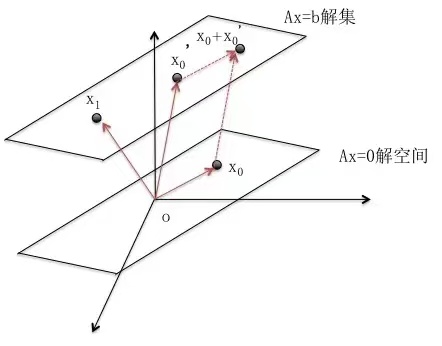
$Ax=b$的解集是一个和$Ax=0$的解空间相平行的结构，该结构是$Ax=0$的解空间沿着一个特解方向平移的结果。

3.行列式及其应用

性质：行列式有很多性质，但是最基本的是这三个性质：①$det(I)=1$ ②交换两行后，行列式的值相反 ③行列式可以按行提出系数；行列式在每行上都具有线性性质。其它性质都可以由这3条推出。

几何意义及其应用：三阶行列式表示平行六面体的有向体积，二阶行列式表示二维平面平行四边形的有向面积

可以通过证明行列式与其对应的体积具有上面的三个性质来证明。

应用：这个初中应该学过，就是已知三角形3个点的坐标,求三角形的面积，这里直接给出结论。

4.投影和格雷姆-施密特正交化法

投影就是在要投影到的空间中找到与被投影向量最近的一点，本质上是一种线性变换，投影所对应的矩阵为：

$P=A(A^{T}A{)}^{-1}{A}^T$，这是将向量投影到矩阵的列空间中。

特别地，如果矩阵的列空间是一条直线，$$P=\frac{a{a}^T}{a^{T}a}$$,

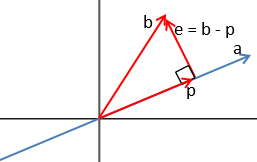
**我们可以证明一下：**假设向量b在a上的投影为p, p=$xa$, e=b-p, 因为e和a是垂直的，所以$a^{T}e=0$,即$a^T(b-xa)=0$,

解得 $x=\frac{a^{T}b}{a^{T}a}$, p=$xa$=$\frac{a^{T}b}{a^{T}a}a=\frac{a{a}^T}{a^{T}a}b$,所以投影矩阵$P=\frac{a{a}^T}{a^{T}a}$

理解了投影后就可以帮助我们理解施密特正交化法。

如何把三个线性无关的向量a,b,c化为标准正交基呢？ 令A=a,B=$b-\frac{A^{T}b}{A^{A}A}A$,C=$c-\frac{A^{T}c}{A^{T}A}-\frac{B^{T}c}{B^{T}B}$,其实就是把原先的向量减去它在另外的向量的投影部分，然后再把A,B,C分别标准化为$q_1,q_2,q_3$即可。

【例2】 $\mathrm{a}=\left[\begin{array}{l}1\\ 1\\ 1\end{array}\right],\mathrm{b}=\left[\begin{array}{l}1\\ 0\\ 2\end{array}\right]$ , 求标准正交矩阵 Q 。

解：根据之前的步骤, $\mathrm{A}=\mathrm{a}=\left[\begin{array}{l}1\\ 1\\ 1\end{array}\right]$ 。

$$\mathrm{B}=\mathrm{b}-\frac{A^{T}b}{A^{T}A}A=\left[\begin{array}{l}1\\ 0\\ 2\end{array}\right]-\frac{3}{3}\left[\begin{array}{l}1\\ 1\\ 1\end{array}\right]=\left[\begin{array}{r}0\\ -1\\ 1\end{array}\right]$$

再进行单位化, 得到标准正交矩阵 Q :

$$Q=\left[\begin{array}{ll}{q}_1& q_2\end{array}\right]=\left[\begin{array}{cc}1/\sqrt{3}& 0\\ 1/\sqrt{3}& -1/\sqrt{2}\\ 1/\sqrt{3}& 1/\sqrt{2}\end{array}\right]$$

5.矩阵的3种分解形式简介

这一部分我们来介绍一下矩阵的LU（对应高斯消元）,QR（对应正交化）分解和SVD（奇异值分解）。

（1）LU分解

将矩阵分解为一个下三角矩阵和一个上三角矩阵。在进行高斯消元时，我们可以通过乘以消元矩阵，我们线代课本上应该叫初等矩阵，比如$E_{21},E_{31},E_{32}$来达到相同的效果,然后我们两边同时乘以消元矩阵的逆，得到A=LU,我们也可以把矩阵U的对角线元素提取出来，分解为一个下三角，一个对角阵，一个上三角，得到矩阵的LDU分解：

下面我们通过一个例子来说明：

【例3】现有 $E_{32}{E}_{31}{E}_{21}\mathrm{A}=\mathrm{U}$ , 已知 $E_{32}=\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& -5& 1\end{array}\right]$, $E_{21}=\left[\begin{array}{ccc}1& 0& 0\\ -2& 1& 0\\ 0& 0& 1\end{array}\right]$, $E_{31}=\mathrm{I}$ ,求 A=L U 分解后的 L 。

思路:$E_{21}$就是第二行减去2倍的第一行，$E_{32}$是第三行减去5倍的第二行，求L就是两边同乘以$(E_{32},E_{31},E_{21}{)}^{-1}$。

​ 逆矩阵化简为: $\mathrm{A}={\left(E_{21}\right)}^{-1}{\left(E_{31}\right)}^{-1}{\left(E_{32}\right)}^{-1}\mathrm{U}$ (注意顺序! )

计算: ${\left(E_{21}\right)}^{-1}=\left[\begin{array}{lll}1& 0& 0\\ 2& 1& 0\\ 0& 0& 1\end{array}\right]$,${\left(E_{32}\right)}^{-1}=\left[\begin{array}{lll}1& 0& 0\\ 0& 1& 0\\ 0& 5& 1\end{array}\right]$

直接代入, $\mathrm{L}={\left(E_{21}\right)}^{-1}{\left(E_{31}\right)}^{-1}{\left(E_{32}\right)}^{-1}=\left[\begin{array}{lll}1& 0& 0\\ 2& 1& 0\\ 0& 5& 1\end{array}\right]$

（2）QR分解

在施密特正交化后我们得到了列空间一组新的基，$A=[a_1,a_2]$,$Q=[q_1,q_2]$,我们两边左乘$Q^T$($Q^{-1}=Q^T$),得到R=$\left[\begin{array}{cc}{a_1}^T{q}_1& {a_2}^T{q}_1\\ {a_1}^T{q}_2& {a_2}^T{q}_2\end{array}\right]$

因为$a_1^T{q}_2=0$,所以R就为上三角矩阵。当然QR分解的方法有很多，除了格雷姆-施密特正交化外，还有Householder变换，吉文斯旋转，感兴趣的读者可以自行学习。

（3）奇异值分解

奇异值分解（Singular value decomposition）将矩阵分解为几个子矩阵相乘，这些子矩阵描述的都是矩阵的重要性质，在图像压缩、信号处理等很多方面都有应用。

定义：任何一个矩阵A都可以写成下面这种形式，$A=U\sum V^T$,U和V都是正交矩阵（列向量是单位正交向量），$\sum$是对角阵，对角线元素是A的非负奇异值，按从大到小排列。

之前我们已经学习过矩阵的对角化，这也被称作特征值分解（EVD），如果是对称矩阵$A=Q\Lambda Q^T$,Q是特征向量矩阵，$\Lambda$的对角线元素是特征值，这对于计算矩阵的幂是很有帮助的,但是对角化的条件是要有n个线性无关的特征向量，这样才能保证Q可逆。

实质：A可以看做是一个线性变换，将行空间的一组正交基变换到列空间中的一组正交基，$A{v}_i={\sigma }_i{u}_i$, ${\sigma }_i$是伸缩系数。

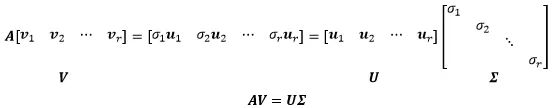
计算：求解挺简单的，U和V分开来求，$A^{T}A=(U\Sigma V^T{)}^{T}U\Sigma V^T=V{\Sigma }^T\Sigma V^T$,$A{A}^T=U\Sigma V^T(U\Sigma V^T{)}^T=U\Sigma {\Sigma }^T{U}^T$,

注：奇异矩阵和长方矩阵也可以进行奇异值分解。对于奇异矩阵A，它的秩一定小于n，所以$A^{T}A$一定是奇异的，从而有一个特征值为0。

6.矩阵与线性变换

问题一：线性变换满足线性性质，设T是一个线性变换，则，从而$T(cv+dw)=cT(v)+dT(w)$，只要满足这两个性质的变换就是线性变换。

问题二：每一个线性变换都可以用一个矩阵来表示，矩阵是和基的选择有关的，如果选择不同的基，线性变换对应的矩阵也会改变。现在假设我们要对二维平面的所有向量进行一个线性变换，我们只需要找到一组基，通过基的线性变换，利用线性性质就可以知道整个空间中的向量的线性变换。如果我们知道输入向量和输出向量，如何找到线性变换所对应的矩阵呢？

令$v_1,v_2,\dots v_n$是输入空间的一组基，$w_1,w_2,\dots w_m$是输出空间的一组基，T对应的矩阵为A。A的第j列元素就是把$v_j$的坐标代入后的输出坐标，下图即

$T\left({\mathbf{v}}_1\right)=a_{11}{\mathbf{w}}_1+a_{21}{\mathbf{w}}_2+\cdots +a_{m1}{\mathbf{w}}_m$

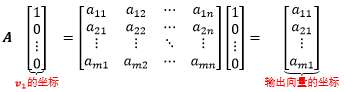
问题三：如何从线性变换的角度来理解对角化和SVD

我们试图找到一个好的基，使一个线性变换对应的矩阵具有好的性质，对角化和SVD其实是一种换基的操作。

定理：假设线性变换T在标准基下对应的矩阵为A（m$\times$ n），现在我们把输入空间的基组成的方阵记为B（n$\times$n），把输出空间的基组成的方阵记为C(m$\times$m)，那么T在新的基下的矩阵为$C^{-1}AB$。

• 如果B=C=S，S为特征向量矩阵，新矩阵为$S^{-1}AS=\Lambda$
• 如果B=V, C=U，新矩阵为$U^{-1}AV=\Sigma$

所以相似矩阵其实是线性变换在不同的基下对应的矩阵，而且我们可以看到如果以特征向量为基，线性变换对应的矩阵为对角阵，对角线上的元素是特征值。

比如我们上面说过的投影矩阵，我们选定该定直线的一个单位向量作为第一个基向量$v_1$，在直线的垂直方向上我们可以取到另一个单位向量作为基向量$v_2$,这两个基向量构成了输入空间和输出空间的一组基，则$T(v_1)=v_1,T(v_2)=0$,投影矩阵为$\left[\begin{array}{cc}1& 0\\ 0& 0\end{array}\right]$.

7.二次型与正定矩阵

首先我们要掌握正定矩阵的四种判断方法：

• 所有特征值都大于0

• 所有主元大于0

• 行列式及所有顺序子式为正（最常用）

• 对任意非零向量$x$,$x^{T}Ax>0$(定义，最重要)

矩阵的二次型：$x^{T}Ax$是含有二次项形式的多项式，我们把它称为矩阵的二次型

**二次型的几何意义：**我们以$A=\left[\begin{array}{cc}2& 6\\ 6& ？\end{array}\right]$为例。

• （1）当？处填入的数大于18时，矩阵是正定的。假设？=20，二次型为$f(x_1,x_2)=2x_1^2+12x_1{x}_2+20x_2^2$,我们可以通过配方化为标准型为$2(x_1+3x_2{)}^2+2x_2^2$,上面我们知道了矩阵的LU分解，$A=\left[\begin{array}{cc}2& 6\\ 6& 20\end{array}\right]=\left[\begin{array}{ll}1& 0\\ 3& 1\end{array}\right]\left[\begin{array}{ll}2& 6\\ 0& 2\end{array}\right]$，我们可以发现配方完的平方项前面的系数就是A的主元，所以主元为正可以判断矩阵正定。如果画出二次型在三维空间的图像如下图，发现它在（0,0）处取得极小值。

  

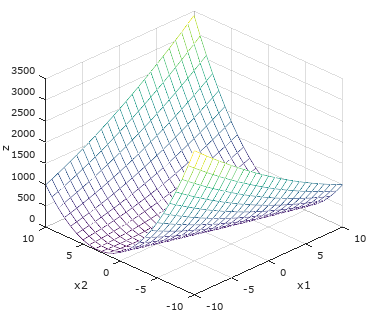
  如果用z=1截切会得到$2x_1^2+12x_1{x}_2+20x_2^2=1$,是一个椭圆，如果A是更高阶的矩阵，那么截切会得到一个椭球，并且椭球轴线的方向就是特征向量的方向，轴线的长度由特征值决定。

• （2）当？处填入的数小于于18时，矩阵不是正定的。假设？=，二次型为$f(x_1,x_2)=2x_1^2+12x_1{x}_2+7x_2^2$，配方后变为$2(x_1+3x_2{)}^2-11x_2^2$,这个图像画出来是一个马鞍面，类似下面这样：

  

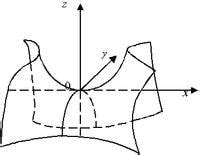
​ 可以看出（0,0）是上曲面的极小值点，是下曲面的极大值点。如果我们用z=1截切会得到一个双曲线。

正定矩阵与极值的关系：我们可以通过判断二阶导数矩阵$\left[\begin{array}{cc}{f}_{xx}& f_{xy}\\ f_{yx}& f_{yy}\end{array}\right]$，（Hessian矩阵）的是正定还是负定来判断极值点。

• $Hessian矩阵是正定阵⟺f_{xx}>0以及f_{yy}{f}_{xx}-2f_{xy}>0$
• $Hessian矩阵是负定阵⟺f_{xx}<0以及f_{yy}{f}_{xx}-2f_{xy}>0$
• $Hessian矩阵是不定阵⟺f_{yy}{f}_{xx}-2f_{xy}<0$

注：负定可以通过特征值都为负数或者奇数阶顺序子式为负，偶数阶顺序子式为正来判断。

简单理解：如果二阶导数矩阵正定，就类似于上面的（1），二阶导数恒为正，类比一元函数正凹负凸，只不过多元函数有好几个二阶导数，这种情况就像一个碗状，所以在那一点取得极小值。如果是负定的话，就是二阶导数的图像翻转一下，所以二阶导数恒小于0。

8.用矩阵解决简单的数学问题

最小二乘法

最小二乘法可以用来拟合一条直线，我们学过Ax=b无解的情况，因为b不在A的列空间中，如果A有n个线性无关的列向量，我们可以两边同时左乘$A^T$,把b投影到A 的列空间中，得到$A^{T}A\hat{x}=A^{T}b$,$A^{T}A$一定是可逆的，所以得到$x=(A^{T}A{)}^{-1}b$；还有一种解决方法是设出直线方程，代入每个点的横坐标值，计算纵坐标差值的平方和，利用二元函数的极值求误差最小值。

【例4】求解（1,1）（2,2）（3,2）拟合的过原点的直线方程。

解：设直线方程为y=kx+b,代入三个点的坐标得，

$\left[\begin{array}{cc}1& 1\\ 2& 1\\ 3& 1\end{array}\right]\left[\begin{array}{c}k\\ b\end{array}\right]=\left[\begin{array}{c}1\\ 2\\ 2\end{array}\right]$，明显方程组无解，两边同时乘以$A^T$,得到$\left[\begin{array}{cc}14& 6\\ 6& 1\end{array}\right]\left[\begin{array}{c}k\\ b\end{array}\right]=\left[\begin{array}{c}11\\ 5\end{array}\right]$，解得$\hat{k}=\frac{1}{2},\hat{b}=\frac{2}{3}$

$\therefore$得到的直线为$y=\frac{1}{2}x+\frac{2}{3}$

解微分方程

利用矩阵的特征值和特征向量可以解决微分方程组，$\frac{d\vec{u}}{dt}=A\vec{u}$的问题。

*【例5】*草原上有一群狼和兔子，数量都为30只，设经过时间t，兔子的数量为r，狼的数量为w，且$\frac{dr}{dt}=6r-2w$,$\frac{dw}{dt}=2r+w$,求经过足够长的时间，兔子的数量与狼的数量之比？

**分析：**狼和兔子的数量变化是耦合的，通过解耦可以求出通解为${\sum }_{i=1}^{\mathrm{n}}{c}_i{e}^{{\lambda }_{i}t}{x}_i$，可以看做是指数函数的线性组合。

解答：(Latex水平有限)

$$\begin{gathered} \overrightarrow{u}=[\begin{array}{c}r\\ w\end{array}],\overrightarrow{u}(0)=[\begin{array}{c}30\\ 30\end{array}],\frac{d\overrightarrow{u}}{dt}=[\begin{array}{cc}6& -2\\ 2& 1\end{array}]\overrightarrow{u} \\ A=\left[\begin{array}{cc}6& -2\\ 2& 1\end{array}\right],易得{\lambda }_1=5,\overrightarrow{x_1}=\left[\begin{array}{c}2\\ 1\end{array}\right],{\lambda }_2=5,\overrightarrow{x_2}=\left[\begin{array}{c}1\\ 2\end{array}\right]\overrightarrow{u}(0)=10\overrightarrow{x_1}+10\overrightarrow{x_2} \\ \therefore \overrightarrow{u}(t)=10e^{5t}\left[\begin{array}{c}2\\ 1\end{array}\right]+10e^{2t}\left[\begin{array}{c}1\\ 2\end{array}\right] \\ \therefore r(t)=20e^{5t}+10e^{2t},w(t)=10e^{5t}+20e^{2t} \\ \therefore \underset{t\to \infty }{\lim }\frac{r(t)}{w(t)}=2 \end{gathered}$$

未完待续！！！

---

结语

这篇文章我觉得有一个缺点就是太简略了，很多知识点都说的不详细，暑假还会再完善一下。线代的学习就要告一段落了，未来还有更多知识等待我去学习，以后也会经常记这种类型的笔记。最后，写这篇文章真的非常不容易，希望各位朋友能点个大大的赞，祝点赞的你早日脱单，逢考必过！！！送你一个大大的柯南。