力扣-数据结构-二叉树-CSDN博客

本文链接：https://blog.csdn.net/2302_80515827/article/details/147618537

94. 二叉树的中序遍历

给定一个二叉树的根节点 root ，返回 它的中序遍历 。

示例 1：

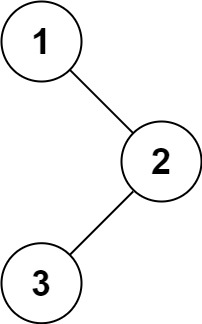
输入：root = [1,null,2,3]
输出：[1,3,2]

示例 2：

输入：root = []
输出：[]

示例 3：

输入：root = [1]
输出：[1]

方法一：递归实现（最简单）

# Definition for a binary tree node.
class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

class Solution:
    def inorderTraversal(self, root: TreeNode) -> list[int]:
        result = []

        def dfs(node):
            if not node:
                return
            dfs(node.left)
            result.append(node.val)
            dfs(node.right)

        dfs(root)
        return result

方法二：迭代实现（使用栈）

class Solution:
    def inorderTraversal(self, root: TreeNode) -> list[int]:
        result = []
        stack = []
        current = root

        while current or stack:
            while current:
                stack.append(current)
                current = current.left  # 一直往左走
            current = stack.pop()
            result.append(current.val)
            current = current.right  # 然后往右走

        return result